Augustin Louis Cauchy

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Augustin-Louis Cauchy, ami de ses aînés Lagrange, Legendre et Laplace, est souvent considéré comme un des plus grands mathématiciens du 19è siècle. Il naquit à Paris le 21 août 1789 au tout début de la Révolution française. La prise de la Bastille avait eu lieu le 14 juillet et la Déclaration des Droits de l'homme et du citoyen le 4 août de cette année là. Le père d'Augustin, Louis-François Cauchy, auparavant avocat au Parlement de Rouen, était le secrétaire du lieutenant général de la police de Paris, Thiroux de Crosne, un poste à haut risque pour ce dernier qui le conduit à l'échafaud. Prudent, Cauchy père, accompagné de sa famille, se démet de ses fonctions, quitte Paris pour Arcueil (petite ville au sud de Paris) où il possède une propriété et se consacre à l'éducation de ses six enfants.

Augustin est principalement formé aux Lettres classiques, au grec et au latin sans écarter les sciences dont tout particulièrement les mathématiques pour lesquelles il fait montre de capacités exceptionnelles. L'arrivée au pouvoir de Napoléon Bonaparte voit le retour de la famille Cauchy à Paris en 1800. Louis-François y sera secrétaire général du tout nouveau Sénat "conservateur" (» réf. 1d).

Augustin entre à l'École centrale du Panthéon (créée en 1795 sur le vœu de Condorcet), qui deviendra le lycée Henri IV sous Napoléon, lequel avait instauré (1802) la classe de mathématiques transcendantes laquelle prépare l'accès, sur examination, aux Écoles Polytechnique et Normale Supérieure mises en place par Monge et Carnot en 1794. C'est ainsi qu'Augustin Cauchy, à peine âgé de 16 ans, entre à l'École Polytechnique (1805), sur examination favorable de Charles Louis Dinet (1775-1856, » réf.2). Il en sort à 18 ans et opte pour l'École (impériale) des ponts et chaussées (1807).

Il se fit connaître deux ans plus tard (1809), en démontrant élégamment la fameuse formule de Descartes-Euler : S - A + F = 2 relative aux polyèdres convexes où S, F et A désignent les nombres de sommets, de faces et d'arêtes. Cauchy en déduit qu'il ne peut exister que cinq polyèdres convexes réguliers constructibles à la règle et compas (au sens d'Euclide).
On lui doit aussi (1813) la preuve du théorème des nombres polygonaux énoncé par Fermat, mais non prouvé, selon lequel tout entier est somme d'au plus n nombres polygonaux d'ordre n distincts ou non.

Cauchy travailla sur le projet du canal de l'Ourcq (mis en chantier en 1802 pour le transport du bois et l'alimentation en eau de la ville de Paris) ainsi qu'à la construction du port de Cherbourg mais il préférera, l'année de son admission à l'Académie des sciences (1816), s'adonner à la recherche et enseigner au Collège de France (physique, mathématique), à l'École Polytechnique (analyse et mécanique) et à la Sorbonne (mathématiques). On luit doit la première théorie mathématique de l'élasticité (1822).

Le collège de France :

Le Collège de France (» réf.16) fut fondé par François Ier en 1530 à l'initiative de Guillaume Budé sous l'appellation initiale de Collège royal. Les cours sont publics. Tous les savoirs (52 chaires actuellement) y sont enseignés par les plus éminents spécialistes nommés par le Chef de l'État. Cette institution purement culturelle ne prépare à aucun examen ou concours et ne délivre aucun diplôme.

La carrière de Cauchy fut contrariée par les événements politiques : disgracié à la révolution de 1830 qui détrôna Charles X au profit du duc d'Orléans, Louis-Philippe Ier, il quitte la France pour l'Italie : il enseigna à l'université de Turin où une chaire de mathématiques est créée à son intention, puis à Prague où il fut le tuteur du jeune Henri d'Artois, petit-fils du roi Charles X, exilés là sous la protection de la famille impériale autrichienne (empire austro-hongrois). Charles X meurt du choléra en 1836. Cauchy retrouvera une chaire d'astronomie à la faculté des sciences de Paris en 1838, qu'il quitte en 1852 suite au coup d'État de Louis-Napoléon Bonaparte du 2 décembre 1851 (alors président de la République) voulant rétablir l'empire français. Ce n'est qu'en 1854 que Cauchy retrouvera son poste auquel Puiseux succédera.

Cauchy rénova l'analyse fonctionnelle réelle dont l'intégrale définie où il exprime des conditions d'existence (y compris pour les solutions d'équations différentielles) et l'étude des suites et séries numériques. Mais le couronnement des travaux de Cauchy réside sans conteste dans la création totalement nouvelle de la théorie des fonctions d'une variable complexe (» IV), leur intégration (» V) et la théorie des résidus, relative à l'intégration d'une telle fonction sur un contour, qu'il développera pendant plus de trente ans, entre 1814 et 1846, ramenant le calcul d'une intégrale à un simple calcul de coefficients et applicable dans le domaine réel ou complexe.

i Le titre de baron (titre de noblesse) fut octroyé à Augustin Cauchy en 1834 par le roi Charles X lors de son séjour à Prague, sous la protection de François Ier d'Autriche, en remerciement de son dévouement dans l'éducation de son petit fils Henri d'Artois tant en matière scientifique que littéraire et philosophique.

I- Les Cours d'Analyse, vers la rigueur :

Cauchy publia (1821) son Cours d'analyse et son Résumé des leçons sur le Calcul infinitésimal (1823, » réf.7) qui eurent très grande audience et constituèrent le premier exposé rigoureux sur les fonctions numériques. Cauchy formalise, en particulier, des notions fondamentales, en particulier :

♦ Notion de limite :

Si les valeurs successivement attribuées à une variable s'approchent indéfiniment d'une valeur fixe, de manière à finir par en différer aussi peu que l'on voudra, alors cette dernière est appelée la limite de toutes les autres.

Cauchy utilise couramment l'abréviation lim placée devant la variable pour préciser sa limite, une notation initiée par Lhuilier. Voici l'exemple donné par Cauchy de sinα/α lorsque α converge vers 0 :

Cette variable, se présente sous la forme indéterminée 0/0 et pourtant possède une valeur fixe que l'on peut calculer ainsi : On a évidemment, pour de très petites valeurs numériques de α :

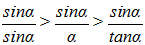
Par conséquent, le rapport sinα/α, toujours compris entre les deux quantités sinα/sinα = 1 et sinα/tanα = cosα, dont la première sert de limite à la seconde, aura lui-même l'unité pour limite.

i Le lecteur pourra vérifier la preuve de Cauchy. Pour l'encadrement, on se limitera à des constatations graphiques. On se penchera sur sa validité eu égard au signe de α.

Quelques limites "usuelles" : »

♦ Fonction d'une variable :

« Lorsque des quantités variables sont tellement liées entre elles, que, la valeur de l'une d’elles étant donnée, on puisse en conclure les valeurs de toutes les autres, on conçoit d’ordinaire ces diverses quantités exprimées au moyen de l'une d’entre elles, qui prend le nom de variable indépendante; et les autres quantités, exprimées au moyen de la variable indépendante, sont ce qu’on appelle des fonctions de cette variable. »

♦ Continuité sur un intervalle :

« h désignant une quantité infiniment petite lorsque, la fonction f(x) admettant une valeur unique et finie pour toutes les valeurs de x comprises entre deux limites données, la différence f(x + h) - f(x) est toujours entre ces limites une quantité infiniment petite, on dit que f(x) est une fonction continue de la variable x entre les limites dont il s’agit. »

➔ Intuitivement et graphiquement, ce résultat exprime que l'on peut décrire la courbe représentative de f sans lever le crayon : pas de "sauts", pas de "trous".

Sur le schéma ci-dessous, on a deux arcs de courbe "continus", et pour passer de l'un à l'autre, lorsque x = 1, il faut "lever" le crayon. Le point de coordonnées (1;0,5) a été renforcé pour préciser que l'image de 1 est 0,5 sur l'arc de gauche et non pas 1 sur celui de droite. La fonction f est ici définie par :

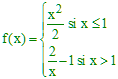
➔ Les définitions plus rigoureuses de limite et de continuité ("avec les ε" comme disent les étudiants) seront le fait de l'allemand Weierstrass (1861). La formalisation usant des quantificateurs et des symboles logiques apparaîtra avec Bourbaki.

♦ Dérivabilité (d'une fonction continue)

Si, lorsque h devient infiniment petit le rapport aux différences :

admet une limite finie, on le note f '(x), c'est une fonction de x, appelée fonction dérivée.

A propos du prime pour désigner la fonction dériver (écriture f'), Cauchy parle de notation "accentuée" (Lagrange parlait de fonction prime) et que l'on peut aussi écrire y' s'il n'y a pas d'ambigüité relativement à la fonction étudiée.

» Rolle , Leibniz , Newton , d'Alembert , Lagrange (notation & sens de variation d'une fonction

Ces définitions permettent à Cauchy d'être le premier à établir rigoureusement la formule de Taylor en précisant les conditions de convergence vers la fonction développée. Toutefois, l'ensemble R des nombres réels n'est pas encore construit. Un nombre réel, à cette époque, est un nombre non imaginaire : entier, fractionnaire ou irrationnel.

Les nombres π et e sont irrationnels depuis Euler et Lambert mais pas encore transcendants. Il faudra attendre Lindemann et Liouville. Le flou entourant les nombres "réels" conduit Cauchy à des conclusions pouvant apparaître comme peu rigoureuses, voire fausses, comme, par exemple, son résultat sur la somme d'une série de fonctions selon lequel toute somme f = Σf_nde fonctions f_n continues en un point x_o est elle-même continue en x_o : la convergence uniforme, nécessaire ici, sera définie par Weierstrass.

La continuité uniforme sera le fait de Heine. Cauchy utilisait également implicitement que, hormis en quelques points singuliers, toute fonction continue admet une dérivée. Riemann, puis Bolzano et Weierstrass donneront un exemple de fonction continue en tout point d’un intervalle et n’étant pourtant dérivable en aucun point.

∗∗∗
Dérivée non continue : étude de la fonction f : x → x²cos(1/x) , Étude de fonctions

Cauchy traite par ailleurs des intégrales définies et indéfinies, des méthodes différentielles, du calcul sur l'exponentielle et le logarithme complexes, des formules de Maclaurin et de Taylor (leçons 36 à 39) qu'il exprime sous les formes actuelles :

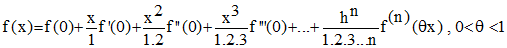
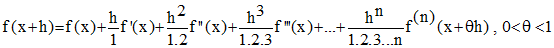
♦ Contre-exemple de Cauchy :

Maclaurin et Taylor n'avaient pas établi de conditions de convergence. Dans sa 38è leçon, Cauchy étudie ce problème et donne un exemple de développement de Taylor convergent, mais non vers la fonction initiale, à savoir f : x → e^-1/x² avec la valeur de continuité f(0) = 0.

Contre-exemple de Cauchy : »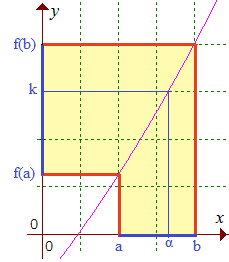

♦ Le théorème des valeurs intermédiaires :

Cauchy énonce et démontre (Cours d'analyse, 1821) ce résultat fondamental :

Si une fonction f est continue entre les limites a et b et que l'on désigne par k une quantité intermédiaire entre f(a) et f(b), on pourra toujours satisfaire l'équation f(x) = k pour au moins une valeur α de x comprise entre a et b.

Autrement dit et plus généralement, car l'image d'une partie connexe par une fonction continue est connexe :

Soit f une fonction numérique continue sur un intervalle I, borné ou non, alors J = f(I) est un intervalle et f prend donc au moins une fois toute valeur comprise entre ses bornes f(a) et f(b):

∀ y∈ J, ∃ x∈ I , y = f(x).

♦ Corollaire :

Si f est strictement monotone sur I (croissante ou décroissante), x est unique (f est une bijection de I sur J).

On a en conséquence le théorème de Bolzano sur l'existence d'un zéro permettant de résoudre les équations du type f(x) = 0 lorsque x est un zéro isolé dans un intervalle [a,b] pour lequel f(a) × f(b) est négatif.

Accroissements finis et th. de la moyenne : » Formules de la moyenne : »

II - Suites et séries, suites de Cauchy :

Cauchy affine également les concepts de suite et de série numériques (à valeurs dans R) ainsi que leurs conditions de convergence dans ses cours à l'École polytechnique (1823). Une suite (u_n) est dite convergente si la fonction n → u_n qu'elle représente admet une limite finie lorsque n tend vers l'infini. Une série est convergente si la suite de ses sommes partielles est convergente. Il expose dans ce cours son célèbre critère de convergence pour les suites numériques :

♦ Critère de Cauchy pour les suites numériques :

ε désignant un nombre arbitrairement petit et positif, une suite de Cauchy est une suite numérique (u_n) pour laquelle |u_m - u_p| < ε à partir d’un certain rang N_ε (c'est à dire dès que m > N_ε, p > N_ε). Il est clair que :

Toute suite convergente est une suite de Cauchy

Inversement, toute suite de Cauchy réelle ou complexe (à valeurs dans R ou C) est convergente et la définition précédente devient le critère de convergence de Cauchy.

Depuis les travaux de Banach, on généralise le concept de suite de Cauchy aux espaces vectoriels normés complets (espaces de Banach), en particulier les espaces fonctionnels (dont les éléments sont des fonctions).

En savoir plus sur les suites, la convergence, les suites de Cauchy : » » Fréchet , Hilbert , Banach

Concernant les séries convergentes de fonctions continues, Cauchy avança imprudemment, dans son cours d'analyse de 1821, que leurs sommes sont continues. Ce qui s'énoncerait :

Si les f_n sont continues au point x_o et si la série Σf_n(x) est convergente dans un voisinage V de x_o, alors la fonction limite f ainsi définie dans V est continue en x_o :

En 1826, Abel corrigea cette affirmation au moyen d'un contre-exemple relativement simple en considérant la série de fonctions de terme général :

Séries, convergence, critères de Cauchy, produit de Cauchy : »

III - Intégration selon Cauchy (cas d'une fonction réelle) : » Intégrale complexe | Intégrale selon Riemann

Entre 1814 et 1825, Cauchy travaille sur la notion d'intégrale sur un intervalle fermé borné suite aux travaux de Leibniz et de Newton établissant le lien entre dérivée, primitive et aire sous la courbe. Il formalise l'intégrale d'une fonction continue sur un intervalle fermé en se détachant, et c'est tout à fait nouveau, tant du lien géométrique (aire) que du lien avec la dérivation (Résumé des leçons sur le Calcul infinitésimal (1823, 21è leçon, page 81, » réf.7). Dès lors est née une théorie moderne de l'intégration qui sera revisitée, en particulier, par Riemann (1854), puis Lebesgue (1902).

Toutefois, dans sa démonstration quant à la convergence de S définie ci-dessus :

S= (x₁ - x_o)f(x_o) + (x₂ - x₁)f(x₁) + (x₃ - x₂)f(x₂) + ... + (x_i - x_i-1)f(x_i-1) + (x_i+1 - x_i)f(x_i) + (X - x_n-1)f(x_n-1)

Cauchy utilise implicitement la continuité uniforme (» Heine) de f sur l'intervalle [x_o,X], ce qui n'est pas faux en l'occurrence puisque cet intervalle est fermé et borné, mais peut engendrer de fausses conclusions lorsqu'il s'agira de passer à la limite sur des intervalles dont une borne (au moins) pose problème.

i Rappelons aussi que Cauchy pensait qu'en dehors de cas pathologiques, toute fonction continue est dérivable, résultat démenti par Weierstrass, et que la somme d'une série de fonctions continues est continue, résultat démenti par Abel. Mais ses Cours d'analyse et ses Leçons sur le calcul infinitésimal, d'une impressionnante modernité, sont un vrai régal et ont justement permis de poser et résoudre ces problèmes subtils que personne avant lui n'avait soulevés.

Au vu de la somme S, il s'agit bien implicitement d'établir le lien entre l'intégrale et l'aire sous la courbe lorsque f est positive sur l'intervalle considéré. Elle est remplacée par une fonction en escalier et S représente la somme des aires des rectangles. Sous les conditions imposées que les différences deviennent très petites lorsque "n est très considérable", les portions d'aires de rectangles en excès et en manque s'amenuisent : S converge vers l'aire sous la courbe.

Afin de prouver le lien fondamental entre fonction primitive, fonction dérivée et intégration, Cauchy définit la notion d'intégrale indéfinie (page 101) :

Comme on peut le lire, Cauchy étudie, usant d'un langage très moderne, les propriétés de la fonction :

et prouve tout d'abord que F'(x) = f(x).

La formule 19 de la 22è leçon (page 87) utilisée à cette fin n'est autre que le théorème de la moyenne établi par Lagrange vingt-cinq ans auparavant :

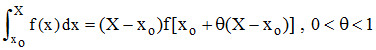
Et la formule 7 de la 23è leçon (page 90) est l'additivité de l'intégrale :

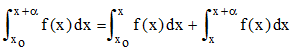
Ayant résolu l'équation différentielle dy = f(x)dx en montrant que F(x) en est solution au même titre que toute autre fonction G différant de F d'une constante additive arbitraire C, soit G(x) = F(x) + C, Cauchy aboutit alors, sans parler de fonction primitive, comme le fit Lagrange, à la formule fondamentale :

Le calcul de Cauchy pour obtenir F'(x) = f(x) est semblable à celui utilisé en classe de Terminale S, sans faire appel aux sommes du type Σ(x_i+1 - x_i)f(x_i) que l'illustre mathématicien allemand Bernhard Riemann introduira en 1854 dans une approche plus sophistiquée pour l'intégration des fonctions bornées, coïncidant avec celle de Cauchy pour les fonctions continues.

Par définition :

Si f est continue et positive un intervalle [a,b], on appelle intégrale de f sur [a,b] l'aire comprise entre la courbe, l'axe des abscisses et les droites x = a et x = b : aire "sous la courbe", nombre évalué en unités d'aire, donc indépendamment de toute unité choisie sur les axes.

Si f est négative sur [a,b], l'intégrale sera l'opposé de l'intégrale de - f. Si f change de signe sur [a,b], son intégrale sera la somme des intégrales calculées sur chaque sous-intervalle où elle garde un signe constant.

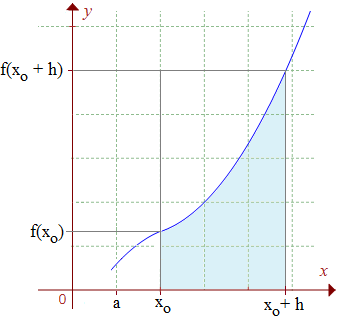
La démarche utilisée contourne le théorème de la moyenne au profit de ce qu'on appelle au lycée le théorème des gendarmes : supposons f continue sur [a,b] contenant le sous-intervalle [x_o, x_o + h] sur lequel f est positive et croissante (h > 0). Notons A(x) l'aire sous la courbe calculée sur l'intervalle [a,x]. L'aire sous la courbe (en bleu) sur [x_o, x_o+ h] s'écrit alors A(x_o+ h) - A(x_o) et on a l'encadrement :

h × f(x_o) ≤ A(x_o+ h) - A(x_o) ≤ h × f(x_o + h)

Divisons par h :

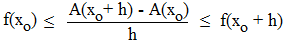
On reconnaît là le taux d'accroissement de A sur l'intervalle [x_o, x_o+ h]. Faisons tendre h vers 0. La fonction f est continue; par conséquent f(x_o + h) a pour limite f(x_o) et le théorème des gendarmes permet de conclure à la dérivabilité de x →A(x) en x_o et on a :

A'(x_o) = f(x_o).

Intégration selon Riemann et propriétés de l'intégrale : »

♦ Formule d'intégration par parties :

C'est encore dans son Résumé des leçons sur le Calcul infinitésimal (1823, 27è leçon) que Cauchy énonce sa formule d'intégration par parties , formule tant fondamentale que pratique et particulièrement simple à prouver, disparue des programmes de Terminale (y compris la Ter S...) depuis 2011 :

En effet, partant de la formule de dérivation d'un produit de deux fonctions dérivables u et v sur l'intervalle [a,b], à savoir (uv)' = u'v + uv', on déduit immédiatement, lorsque u' et v' sont continues sur [a,b] :

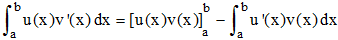
On peut préférer l'écriture différentielle plus condensée :

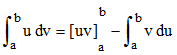
➔ L'intégration par parties est un outil extrêmement efficace : lors de l'intégration d'un produit de deux fonctions f et g, si l'on connaît les primitives de l'une, par exemple g, mais pas de l'autre, on tente de résoudre le problème en posant u = f et v' = g, ce qui conduit à rechercher une primitive non plus de f × g mais de f ' × ∫g. Mais cela "ne marche pas "à tous les coups" : il se peut fort bien que le u'v de la formule ne soit pas facilement intégrable...

i En classe terminale, la locution "en utilisant une intégration par parties, calculer l'intégrale ..." est remplacée par un énoncé du type :

a) Calculer la fonction dérivée de...
b) En déduire les primitives de ... ou bien b) En déduire l'aire ...

Exemple : calcul des primitives de x → ln x :

a) Soit x > 0. Calculer la fonction dérivée de la fonction x → x.ln x
b) En déduire la primitive de x → ln x qui s'annule en x = e.
Rép. : a) (xln x)' = ln x + 1.
          b) On déduit de a) que ln x = (x.ln x)' - 1. Soit x > 0, en intégrant cette identité sur [e,x], on obtient :

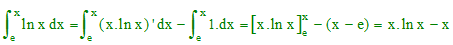
La fonction ln, logarithme népérien : »

Critère de Cauchy pour la convergence d'une intégrale généralisée (» intégrale généralisée) :

Soit f une fonction continue sur tout intervalle fermé [a,u], u > a. L'intégrale de f sur [a,+∞[ est convergente (» intégrale généralisée) si et seulement si :

∀ ε > 0, ∃ u > a : (x > u , x' > u) ⇒ ∫_[x,x'] f(t)dt < ε

En utilisant ce critère et la seconde formule de la moyenne (seconde formule de Bonnet), on peut prouver ce théorème très utile :

Si f est positive et décroissante sur I = [a,+∞[ avec lim_+∞ f = 0 et g intégrable et bornée sur tout intervalle fini K de I vérifiant
|∫_Kg(x)| ≤ M où M désigne un réel positif indépendant de K, alors l'intégrale généralisée |∫_I f(t)g(t)| est convergente. ☼

De ce résultat, on déduit par exemple que l'intégrale de Dirichlet, intégrale sur R+ de sin(x)/x, est convergente.

Calcul de l'intégrale de Dirichlet : » » Darboux , Lebesgue , Stieltjes

Valeur principale de Cauchy d'une intégrale généralisée (» intégrale généralisée) :

Lorsqu'une fonction numérique présente une singularité (discontinuité, limite inexistante ou infinie) isolée en un point fini x_o d'un intervalle I = [a,b], on peut toutefois chercher à donner un sens à l'intégrale de f sur I :

a) Si, pour h > 0 et k > 0, la somme lim_{h → 0} ∫_{[a,xo
- h]} f(t)dt + lim_{k → 0} ∫_[xo_{+ k}_,b] f(t)dt est un nombre fini L, on dira alors que f est intégrable sur [a,b] et que son intégrale est L.

Si la condition a) s'avère non vérifiée, f est déclarée non intégrable sur [a,b]. On considère cependant le cas particulier k = h :

b) Si, pour h > 0, la somme lim_{h → 0} [ ∫_{[a,xo
- h]} f(t)dt + ∫_[xo_+h_,b] f(t)dt ] est un nombre fini L, on dit que L est la valeur principale de Cauchy de l'intégrale de f sur I et on écrit VP ∫_[a,b] f(t)dt = L.

Dans le cas f(x) = 1/x, de primitive x → ln|x| et [a,b] contenant 0, a) n'est pas vérifiée en x_o = 0, mais lim_{h → 0+} [ ∫_{[a,xo
- h]} f(t)dt + ∫_{[xo
+h}_,b] f(t)dt ] = lim_{h → 0+} [ (lnh - ln|a|) + (ln|b| - lnh) = ln(|b/a|) = VP ∫_[a,b] 1/tdt.

c) Dans le cas d'une fonction F définie par une intégrale, F(x) = ∫_[a,x] f(t)dt, x ≥ a, avec x_o intérieur à [a,x], si la somme lim_{h → 0} [ ∫_{[a,xo
- h]} f(t)dt + ∫_[xo_+h_,x] f(t)dt ] est une fonction x → φ(x), x ≥ a, x ≠ x_o, on dit que φ est la valeur principale de Cauchy de F et on écrit VP ∫_[a,x] f(t)dt = φ(x).

➔ Concrètement, la valeur principale de Cauchy tente d'éliminer la difficulté en x_o par une approche symétrique de la singularité, ce qui correspond géométriquement, en interprétant l'intégrale comme une aire, à sommer une "positive" et une aire "négative" dont le résultat "s'évanouit" (comme on disait autrefois) à la limite.

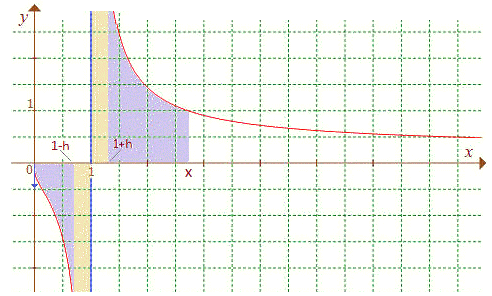
Étude du logarithme intégral, x ≥ 0, Li(x) = ∫_[o,x] 1/ln(t)dt : » » Landau

IV - La théorie des fonctions d'une variable complexe :

Le calcul différentiel et intégral dans le plan complexe prolonge le cas réel mais on y rencontre de grandes difficultés dues au fait que C s'apparente à R² : un subterfuge est alors l'usage des fonctions de deux variables réelles.

♦ Conditions de Cauchy pour la dérivation (également dites de Cauchy-Riemann) :

La dérivabilité se définit comme dans le cas réel par usage du taux d'accroissement. En notant Δz = z - z_o et et Δf = f(z) - f(z_o), f est dite dérivable (en z_o si le rapport Δf/Δz admet une limite finie quelle que soit la façon dont z tend vers z_o dans le plan complexe.

Cette limite est alors noté f '(z_o), nombre dérivée de f en z_o. On disait à l'époque que f est monogène en z_o.

➔ Dire que Δz tend vers 0 signifie que le module de Δz, à savoir |z - z_o|, tend vers 0. Concernant ces fonctions complexes, Cauchy parlait de fonction monogène en z_o plutôt que de fonction dérivable. Cette terminologie perdura jusqu'aux années 1950. Notons ici que l'on doit à Cauchy le terme d'argument d'un nombre complexe (1838), terme emprunté à l'astronomie mesurant l'angle de la position de la lune sur son orbite compté à partir du point où cette orbite coupe celle de la Terre (Encyclopédie de d'Alembert et Diderot, 1752).

» Argand , Wessel.

De manière équivalente, on peut exprimer la dérivabilité en z_o par l'existence d'une fonction ε de la variable z telle que :

Δf = [f '(z_o) + ε(z)] × Δz avec ε(z) → 0 quelle que soit la façon dont z tend vers z_o dans C.

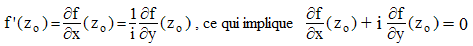On peut alors choisir de faire tendre z vers z_o en posant z = z_o + x, x réel tendant vers 0, ce qui fournit Δf = [f '(z_o) + ε(z)] × Δx ou bien en posant z = z_o + iy, y réel tendant vers 0, ce qui fournit Δf = [f'(z_o) + ε(z)] × iΔy et le passage à la limite conduit aux égalités :

(fp) » notion de dérivée partielle

Dans le cas fréquent où f(z) peut se mettre sous la forme P(x,y) + iQ(x,y) en séparant les parties réelle et imaginaire, la dérivabilité de f nécessite la dérivabilité partielle des fonctions réelles P et Q en x_o et y_o et les égalités (conditions de Cauchy-Riemann) :

(ccr)

Ces conditions nécessaires pour la dérivabilité en un point s'avèrent suffisantes. Plus précisément :

En posant z = x + iy et f(z) = P(x,y) + iQ(x,y), une condition nécessaire et suffisante de dérivabilité de f en un point z_o est que P et Q soient différentiables en z_o et vérifient en ce point les conditions (ccr) ci-dessus. On a alors selon (fp) :

En termes d'opérateurs de dérivation, en posant :

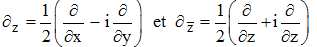on remarquera que f'(z_o) = ∂_zf(z_o) et que les conditions de Cauchy peuvent se résumer à ∂_z f(z_o) = 0, z désignant le complexe conjugué de z.

» Riemann , Morera Dfférentielle exacte : »

♦ Harmonicité :

Les conditions de Cauchy-Riemann impliquent immédiatement que les fonctions P et Q sont harmoniques :

Laplacien (notation Δ) : »

Dans son Calcul infinitésimal de 1823, Cauchy définit le logarithme complexe en utilisant la notation z = x + √-1.y ou bien la forme trigonométrique z = r(cosθ + √-1.sinθ). Gauss systématisera (1831) l'usage de z = x + iy (i, comme imaginaire, est la notation d'Euler pour √-1).

♦ Fonction analytique, fonction entière et fonction holomorphe, dite "synectique" par Cauchy :

Une fonction de C dans C est dite holomorphe sur un ouvert U de C si elle est uniforme sur U (chaque image est unique, ce qui n'est pas toujours le cas) et dérivable en tout point de U (au sens défini ci-dessus).

» Holomorphe, holomorphie : du grec holo = entier et morphê = forme, appellation due à Bouquet en remplacement de synectique (du grec sunektikos = compréhensif) proposé par Cauchy.

➔ Les conditions d'harmonicité de P et Q explicitées ci-dessus permettent de prouver que deux fonctions holomorphes ayant même partie réelle diffèrent d'une constante imaginaire pure.

! Ne pas confondre fonction uniforme (dont toute image est unique, terme dû à Hermite, dite monotypique par Cauchy) et fonction univalente : il s'agit alors d'une fonction holomorphe (uniforme et dérivable) et injective (des images égales ont des antécédents égaux).

» Bieberbach Fonctions méromorphes : » Fonctions multiformes et surfaces de Riemann : »

Une fonction (réelle ou complexe), est dite analytique (terme dû à Condorcet) en un point x_o intérieur à son ensemble de définition U si elle est développable en série entière dans un voisinage de x_o : il existe une série Σa_n(x - x_o)ⁿ, n ≥ 0, convergeant vers f(x) dans un voisinage de x_o inclus dans U.

Les fonctions holomorphes sur U coïncident avec les fonctions analytiques sur U, c'est à dire développables en série entière car contrairement aux fonctions numériques (réelles), en conséquence du théorème de Cauchy-Goursat énoncé ci-après :

Toute fonction complexe continument dérivable sur U est infiniment dérivable sur U

Une fonction holomorphe en tout point de C est dite entière : elle est développable en série entière Σa_nzⁿ en tout point de C.

Par exemple, la fonction exponentielle z → e^z est une fonction entière.

La somme f + g, le produit f.g et le quotient f/g (dans ce dernier cas si g ne s'annule pas sur U) de fonctions holomorphes est holomorphe.

♦ La conservation des angles, une propriété des fonctions holomorphes (transformations conformes) :

Une propriété fondamentale des fonctions holomorphes est la conservation des angles. Plus précisément :

Soit z → f(z) est holomorphe sur un ouvert U contenant z_o et f '(z_o) ≠ 0. Si (C₁) et (C₂) sont deux courbes admettant une tangente en z_o, alors l'angle orienté entre ces tangentes est le même qu'entre les tangentes en f(z_o) aux courbes images f(C₁) et f(C₂).

On exprime cette importante propriété en parlant de transformation conforme :

Mercator Gerhard Kremer : » » Lelong-Ferrand , Bierberbach , Morera

♦ Inégalité de Cauchy et conséquences :

Soit f une fonction holomorphe non constante et non réduite à un monôme sur un domaine D contenant O, et Σa_nzⁿ son développement en série entière de rayon de convergence R. Alors, en notant M(r) le maximum de | f(z) | pour |z| = r, on a pour tout n de N : | a_n | < M(r)/rⁿ.

Remarque : si f se réduit à un monôme αzⁿ, l'inégalité ne s'applique pas : dans ce cas M(r)/rⁿ = |α|.

Conjecture de Denjoy : »

On a en conséquence :

1. Si une fonction f, non constante, est holomorphe sur U ainsi que sur sa frontière F, alors le maximum
de |f(z)| sur U∪F est atteint en un point de F.

2. Les théorèmes de Cauchy-Liouville :

a/ Toute fonction entière (holomorphe sur C tout entier) et bornée est constante.
b/ Soit k un entier non nul, si lim_r→∞ M(r)/r^k = 0, alors f est un polynôme de degré k.

3. Si f est une fonction holomorphe sur un domaine D borné du plan complexe ainsi que sur sa frontière, alors f admet un nombre fini de zéros dans D.

♦ Ordre d'une fonction entière :

Selon l'inégalité de Cauchy énoncée ci-dessus, si f est entière, on a M(r)/rⁿ > | a_n | pour tout n de N. C'est dire que le maximum de | f | sur le disque |z| = r, qui est une fonction croissante de r, se comporte vis à vis des puissances n-èmes de r comme une exponentielle de r. D'où l'idée, due à Émile Borel, de classer les fonctions entières selon la comparaison du logarithme de M(r) par rapport à r, ce qui revient à comparer loglogM(r) par rapport à Log r en définissant l'ordre ρ de f par :

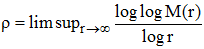
Pour une fonction méromorphe sur un disque |z| < R (rayon de convergence de sa série, son ordre ρ est définie par :

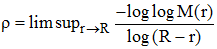
Les notions de limite inférieure et supérieure : »

V - L'intégration des fonctions complexes :

Considérons une fonction complexe z → f(z) avec z = x +iy et f(z) = P(x,y) + iQ(x,y). La définition de l'intégrale de f sur un arc de courbe continu (c), fermé ou non, d'origine A, d'extrémité B sur lequel on aura choisi un sens de parcours positif (celui des abscisses curvilignes croissantes) se définit comme dans le cas réel à la manière de l'intégrale réelle selon Cauchy ou Riemann.

Ces sommes S_n s'écrivent ici :

S_n= (z₁ - z_o)f(c₁) + (z₂ - z₁)f(c₂) + (z₃ - z₂)f(c₂) + ... + (z_n - z_n-1)f(c_n)

Les z_k forment une subdivision de l'arc de courbe (c) et si ces sommes admettent une limite lorsque Max |z_k - z_k-1| tend vers 0, on démontre que cette limite ne dépend ni de la subdivision, ni du choix des c_k. On l'appelle intégrale de f sur (c) et on écrira :

En savoir plus sur l'intégrale complexe : » Calcul des résidus : » » Goursat , Morera

Loi de Cauchy (calcul des probabilités) :

Il s'agit de la loi de probabilités continue, définie de densité :

Sachant que x → 1/(1 + x²) est la fonction dérivée de la fonction Arc tangente, x→Atn x, fonction réciproque de la fonction tangente sur l'intervalle ]-π/2, +π/2[, on a (en tenant compte de l'imaprité) :

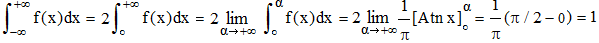
! Pour qu'une fonction soit intégrable sur R tout entier (» intégrale généralisée) , il faut et il suffit qu'elle soit intégrable sur ]-∞,0] et sur [0,+∞[, c'est à dire sur ]-α,0] et sur [0,+α[ et que la convergence soit assurée en faisant tendre α vers l'infini.

La fonction de répartition, définie de R sur ]0,1[, est :

♦ Espérance mathématique (moyenne), variance :

Cette loi n'a ni moyenne, ni variance :

Concernant l'espérance mathématique, à un facteur multiplicatif près, une primitive de xf(x) est x→ln(1 + x²) qui diverge sur ]-∞,0[ et [0,+∞[. » fonction logarithme
Concernant la variance, à un facteur multiplicatif près, une primitive de x²f(x) est x→x - Atn x. Par parité, on se ramène à une intégrale sur [0,+∞[ qui diverge (Atn x est bornée mais non pas x).

La notion d'intégrale généralisée (bornes infinies) : »

Remarques :

On peut cependant calculer la médiane, à savoir m_d tel que F(m_d) = 1/2, ce qui implique Atn(m_d) = 0 : la médiane est nulle.
On est en présence d'une loi de Student à 1 degré de liberté.
On rencontre en sciences physiques la distribution de Lorentz (H. Lorentz, physicien hollandais, 1853-1928) dans des phénomènes de résonance avec une forme plus générale :

les nombres s et t sont respectivement les paramètres d'échelle et de position.

∗∗∗
Phénomène aléatoire suivant une loi de Cauchy (distribution uniforme sur le cercle)

Notions sur les lois de probabilités continues : »

Équations différentielles :

Cauchy met en place une vaste théorie des équations différentielles et aux dérivées partielles : existence, recherche et unicité des solutions, couronnement des travaux des grands mathématiciens qui le précédèrent comme Leibniz, les Bernoulli, Euler, Riccati, Lagrange.

♦ Problème de Cauchy ou problème aux conditions initiales :

Lorsqu'on résout une équation différentielle, comme par exemple y'y = x, il apparaît des constantes arbitraires : on a ici 2yy' = 2x, d'où y² = x² + C, C désignant un nombre réel quelconque. On peut cependant vouloir, dans un problème particulier, imposer des conditions aux solutions. C'est le problème de Cauchy, également appelé problème aux conditions initiales, faisant allusion à la résolution de problèmes concrets en sciences physiques.

Le problème de Cauchy se résume alors à la recherche d'une fonction y = φ(x) définie sur un intervalle J de R, fini ou non, de fonction dérivée f' vérifiant :

où f désigne une relation fonctionnelle entre x et y = φ(x).

! On ne confondra pas le problème de Cauchy avec le problème plus général et plus difficile des conditions aux limites (ou problème aux limites) : si l'équation différentielle est étudiée sur un intervalle J = [a,b], celle-ci peut être soumise à une (ou plusieurs) conditions portant sur les bornes de J. Par exemple la donnée d'une condition initiale en x = a et d'une condition finale en x = b ou encore une relation fonctionnelle liant x, y , a et b.

➔ Dans le cas élémentaire de l'équation linéaire du 1er ordre d'inconnue y' = a(x)y + b(x), il existe une unique solution y = f(x) au problème de Cauchy, à savoir :

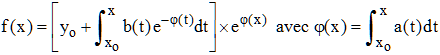
♦ Théorème 0 (Peano) : » Peano

Soit (x,y) → f(x,y) une fonction numérique continue sur un domaine ouvert D de R². Alors, quel que soit (x_o,y_o) dans D l'équation différentielle y' = f(x,y) admet au moins une solution prenant la valeur y_o au point x_o.

♦ Théorème 1 (Cauchy) :

Soit (x,y) → f(x,y) une fonction numérique continue sur un domaine D de R². On suppose qu'en tout point (x,y) de D la fonction f est dérivable par rapport à y et qu'il existe un réel non nul k indépendant de x tel que |∂f(x,y)/∂y| ≤ k. Alors, quel que soit (x_o,y_o) de D, l'équation différentielle y' = f(x,y) admet une unique solution y = φ(x) vérifiant y_o = φ(x_o).

Toute fonction dérivable sur un intervalle J de R, de dérivée bornée par k sur J est lipschitzienne de rapport k (et inversement). Par suite, le théorème suivant, moins fort, assure également l'existence et l'unicité d'une solution. Lipschitz le généralisa aux systèmes différentiels linéaires explicites du 1er ordre.

i Rappelons que si V est un voisinage de (x_o,y_o), la condition de Lipschitz dans V, par rapport à y, s'écrit :
∃ k > 0, ∀(x,y₁)∈V, ∀(x,y₂)∈V, | f(x,y₁) - f(x,y₂) | ≤ k.| y₁ - y₂ |

♦ Théorème 2 (Cauchy-Lipschitz) : » Rudolf Lipschitz

Soit (x,y) → f(x,y) une fonction numérique continue sur un domaine D de R²; on suppose que f est lipschitzienne par rapport à y dans un voisinage d'un point (x_o,y_o) de D. Alors l'équation différentielle y' = f(x,y) admet une unique solution y = φ(x) vérifiant y_o = φ(x_o).

Exemple élémentaire du problème de Cauchy : déterminer les fonctions numériques réelles telles que pour tout x de R, y' = y et f(0) = 1. La réponse est unique : il s'agit de la fonction exponentielle de base e : x → e^x. » approches de la fonction exponentielle.

Méthode des approximations successives de Picard : »

➔ Le problème se complique lorsqu'il s'agit d'une équation différentielle d'ordre supérieur à 1. Dans le cas du second ordre, une équation du type y" = f(x,y) admet là encore au moins une solution y = φ(x) si f est continue. Les conditions initiales seraient ici les données de y_o et y'_o en un point x_o, la solution φ devant vérifier φ(x_o) = y_o et φ'(x_o) = y'_o.

Euler et l'étude de la fonction exponentielle : » » Sofia Kovalevskaïa

Autres contributions :

Inégalité de Cauchy-Schwarz : » Schwarz
Théorie des déterminants (1815-1820) en tant que formes multilinéaires alternées suite aux travaux des précurseurs que furent Leibniz, Lagrange, Vandermonde et, principalement, Cramer. Le terme déterminant, emprunté à Gauss (1801), sera désormais systématiquement utilisé. La voie s'ouvre pour l'introduction des matrices. Ce sera l'œuvre de Cayley et Sylvester (1843) à qui l'on doit (1841) la notation actuelle des déterminants, entre barres comme ci-dessous à gauche :

i Selon, Florian Cajori, un an avant (1840), dans un fascicule d'Exercices d'analyse et de physique mathématique, Cauchy, dont les notations de 1815 n'étaient pas des plus simples et pratiques, utilisa une forme proche pour désigner une forme multilinéaire alternée illustrée ci-dessus à droite.

On doit encore à cet immense mathématicien français que fut Augustin Cauchy :

Une théorie "moderne" des substitutions (1844), le concept de permutation circulaire et des notations annonçant le vocabulaire actuel des groupes institués par Cayley.
Le concept de groupe (1815, le terme est de Galois) dans les premiers grands travaux relatifs à la résolution des équations polynomiales, en tant que structure algébrique restreinte cependant aux permutations : groupes de substitutions sur un ensemble fini que Abel (1826) et Galois (1832, publié en 1846) utiliseront avec succès. Le cas général, axiomatisation de cette notion, sera le fait de Cayley et de Weber.
Un beau théorème, également énoncé et prouvé par Lagrange :

Soit (G,*) un groupe fini d'ordre p, d'élément neutre e, alors :
l'ordre de tout sous-groupe divise p et il existe un élément x de G tel que x^p = e

i l'ordre d'un groupe fini est son cardinal (nombre d'éléments). x^p désigne ici x*x*x..., composé de p éléments égaux à x.

Preuve de cet important résultat : »

∗∗∗

1. niveau TerS : Aire sous la parabole 2. niveau SUP : Intégrale de Wallis
3. Intégration : niveau bac | niveau sup #1 , niveau sup #2 | niveau sup #3.
4. Application du théorème des valeurs intermédiaires à une équation polynomiale de degré 5 , voir aussi voir aussi degré 4

5. Montrer que les primitives de x → ln(x) sont x → x.ln(x) - x + C.
Indication : procéder par parties ou calculer d'abord la fonction dérivée de x → x.ln(x).

6a. Par deux intégration par parties successives , calculer l'intégrale sur l'intervalle [0,1] de la fonction x → x²e^-x. Rép : 2 - 5/e

6b. Calculer les primitives de la fonction x → ln x. Rép : clic...

7.
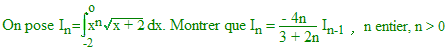
    Calculer I₅ à 10^-2 près. Indications : on calculera I_o et on utilisera la relation de récurrence. Rép : I_o= 4√2/3 et I₅= -32768√2/9009

8. Sachant que -cotan x est une primitive de 1/sin²x (fonction cotangente), calculer les primitives de 1/sin⁴x.
    Indications et réponse : si j(x) désigne les primitives cherchées, on vérifiera, en procédant par parties, que
    j(x) = -cosx/sin³x - 2j(x) + 2∫dx/sin²x. D'où 3j(x) = -cosx/sin³x - 2cotan x = -3cotan x - cotan³x + C

9.
b) Montrer que f ', fonction dérivée de f, vérifie x²f '(x) = f '(x) - 1 pour tout x de ]-1,+1[. Indic. : f '(x) = 1/(1-x²).

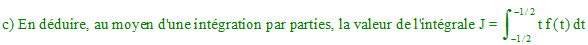
Indications : t → t f(t) étant paire, on peut intégrer sur [0,1/2] et multiplier par 2 le résultat. En posant f(t) = u et tdt = dv,
le terme à intégrer devient t²f '(t) que l'on remplacera par f '(t) - 1, ce qui conduira facilement à J = 1/4 - 3ln(√3)/8 ≅ 0.088.

➔ Pour en savoir plus :

a) Éloge de Augustin-Louis Cauchy par Joseph Bertrand (1898) :
https://tpsalomonreinach.mom.fr/Reinach/MOM_TP_071648/MOM_TP_071648_0002/PDF/MOM_TP_071648_0002.pdf
b) Histoire Abrégée des Sciences Mathématiques, par Maurice d'Ocagne & René Dugas -Éd. Vuibert, Paris - 1955
c) La vie et les travaux du baron Cauchy, par Claude-Alphonse Valson, préface de Ch. Hermite (1868) sur Google Livres :
T1, La vie : https://books.google.fr/books?id=vQ7tw0rVKPsC&printsec=frontcover&pg=PA92&redir_esc=y#v=onepage&q&f=false
T2, Les travaux : https://books.google.fr/books?id=Te0kTJm3HqAC&newbks=0&printsec=frontcover&pg=PR3#v=onepage&q&f=false
d) Le Sénat conservateur sur Wikipédia : https://fr.wikipedia.org/wiki/Sénat_conservateur
Charles Louis Dinet, courte biographie sur Persée : https://www.persee.fr/doc/inrp_0298-5632_1986_ant_11_1_6320
Calcul infinitésimal, Jean Dieudonné, Ch. VII, La théorie de Cauchy, Ed. Hermann, Collection Méthodes - Paris, 1968.
THEORIE des FONCTIONS (réelles et complexes), Georges Valiron, Éd. Masson, Paris - 1942.
Cours de mathématiques, Jean Bass, tome II, Éd. Masson - Paris, 1964.
Calcul différentiel complexe, par Daniel Leborgne - Que sais-je n°2560, Éd. P.U.F.
Résumé des leçons sur le calcul infinitésimal, Augustin-Louis Cauchy
Les cours historiques de l'Ecole Polytechnique (1823), Éd. MARKETING (ellipses) - 1994.
En ligne sur Gallica : http://gallica.bnf.fr/ark:/12148/bpt6k62404287
Calcul infinitésimal, par Jean Dieudonné - Éd. Hermann, Paris 1968
Fonctions analytiques (complexes), cours de Cyrille Barreteau (CEA) et Elie Raphaël (ESPCI)
Analyse complexe, par Ernst Hairer, univ. Genève
http://www.unige.ch/~hairer/poly_complexe/chap1
http://www.unige.ch/~hairer/poly_complexe/chap2 (calcul intégral et théorie de Cauchy)
http://www.unige.ch/~hairer/poly_complexe/chap3 (singularités et fonctions méromorphes, sphère de Riemann)
Analyse complexe, par G. Carlier (univ. Paris Dauphine), fonctions holomorphes, méromorphes, formules de Cauchy, résidus, ...
https://www.ceremade.dauphine.fr/~carlier/analysecomplexe.pdf
Cours de Noëlle Pottier (université Paris 7) :
• Fonctions analytiques complexes : http://www.msc.univ-paris-diderot.fr/~pottier/page2/files/Chapitre_4.pdf
• Intégration complexe : http://www.msc.univ-paris-diderot.fr/~pottier/page2/files/Chapitre_5.pdf
Les généralisations de la notion mathématique d'intégrale au 19è siècle, par Jean-Philippe Villeneuve sur CultureMath (ENS) :
http://culturemath.ens.fr/histoire des maths/htm/villeneuve-2008/villeneuve2008.html
Leçons sur les fonctions entières, par Émile Borel (1900), numérisé sur Internet Archive
https://archive.org/stream/leonssurlesfonc02boregoog#page/n7/mode/2up
Fonctions lipschitziennes (niveau licence/Capes) : http://www.iecl.univ-lorraine.fr/~Gerard.Eguether/zARTICLE/AF.pdf
Site officiel du collège de France :
- http://www.college-de-france.fr/site/college/index.htm
- Département mathématiques : http://www.college-de-france.fr/site/alain-connes/index.htm

Poncelet

Möbius