ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

KREMER Gerhard, alias MERCATOR  Gerardus, flamand, 1512-1594

 !  Ce géographe ne doit pas être confondu avec le mathématicien allemand Nicolaus Kaufmann dit Mercator.

Gerhard Kremer étudia la philosophie et la théologie à l'université de Louvain et s'intéressa à la cartographie. Il se fit connaître en Europe sous le nom latinisé de Gerardus Mercator sans lien apparent avec son nom de famille d'origine (en latin mercator = marchand, commerçant) contrairement au mathématicien Nicolaus Kaufmann (en allemand Kaufmann = marchand) qui emprunta le même nom.

On doit à Mercator les célèbres représentations des globes céleste et terrestre (dès 1541) et la projection dite cylindrique conforme (1565) portant son nom : représentation plane de la Terre en tant que maillage rectangulaire où les méridiens apparaissent parallèles et équidistants, les distances entre les parallèles, augmentant avec la latitude. Le qualificatif de conforme signifiant qu'elle respecte les angles.

Latitude, longitude, coordonnées sphériques : »          

La projection Mercator est dite cylindrique car elle consiste, initialement, à projeter tout point du globe terrestre, assimilé à une sphère sur un cylindre tangent à l'équateur, d'axe (d) nord-sud, perpendiculairement à (d). Après une telle projection, si on développe le cylindre (on le "déroule"), les parallèles projetés, cercles de la sphère parallèles au plan de l'équateur, auront tous la même longueur, ce qui est ennuyeux pour une bonne conformité, car plus la latitude est élevée, plus les parallèles sont "petits". La projection conduit alors à une représentation d'autant plus aplatie et étirée que la latitude est élevée.

Mercator effectue alors une correction entre les distances des parallèles projetés : si R désigne le rayon de la Terre, un parallèle de latitude φ est, par rapport à l'équateur, à la hauteur x = Rsinφ, son rayon r est  Rcosφ.

Le rapport des circonférences est comme r/R = cosφ diminuant lorsque φ augmente, ce qui explique (en partie) les déformations. On décide donc d'appliquer le rapport inverse 1/cosφ. Mais les zones proches des pôles ne sont pas représentables : rejetées à l'infini car cosφ tend vers 0 !

En effet, pour un accroissement dφ de latitude, vu que x = Rsinφ, on a dx = Rcosφdφ : on "rétablit" alors la distance par :

dx = dφ × R/cosφ

Il n'y a plus qu'à intégrer de 0 à φ pour obtenir la distance ("hauteur") des parallèles projetés par rapport à l'équateur de la carte (φ = 0, x = 0). Prenons R comme unité (R = 1) :

La constante d'intégration est nulle puisque si φ = 0, il nous faut x = 0. Cette expression, à un coefficient multiplicatif près, est parfois appelée latitude de Mercator.

Ainsi corrigée, cette projection est conforme pour signifier qu'elle respecte les angles. Elle ne respecte cependant pas les aires : des surfaces de même aire sur la Terre ont généralement des aires distinctes sur la carte, lesquelles augmentent avec la latitude.

 

 ➔  Avec un axe de cylindre nord-sud, cette projection reste acceptable pour des latitudes comprises entre -60° et +60° : en effet, si la latitude φ est proche de π/2, on a encore quelque ennuis car ln |tan(π/2)| devient infini... Pour une carte au voisinage d'un pôle, il s'agira de placer le cylindre de projection tangent en un point proche du secteur étudié. Une projection respectant les aires est dite équivalente, il en est ainsi de la comme la projection Hammer (» ref.6)

∗∗∗
Prouver que x= ln|tan(φ/2 + π/4)| peut aussi s'écrire ½ln[(1 + sinφ)/(1- sinφ)] ou encore Argsh(tanφ)
ou encore Argth(sinφ) ou encore...   » fonctions Argsh, Argth


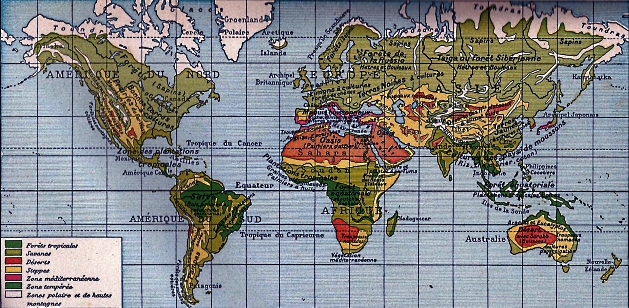
Planisphère obtenue selon la projection de Mercator (Atlas classique Hachette - 1950)

Sur une carte de Mercator, une route maritime coupant chaque méridien sous un même angle est une droite :  on parle de loxodromie (du grec loxos = oblique et dromos = course),  ce qui est pratique pour les navigateurs : à cap constant, on suit un chemin rectiligne sur la carte. Toutefois, ce n'est pas le chemin le plus court : les géodésiques de la sphère sont les arcs de grands cercles (arcs de méridiens). De telles trajectoires sont appelées orthodromies.

 »  Pedro Nonius              Loxodromie et orthodromie : »

La notion de transformation conforme en analyse complexe :   

Au 19è siècle, les fonctions d'une variable complexe seront étudiées tout particulièrement par Cauchy et Riemann. Les difficultés liées à la non uniformité de ces fonctions (non unicité de l'image d'un complexe z) conduisent aux surfaces de Riemann et à la topologie algébrique, dont les applications se rencontrent dans les bureaux d'étude, en construction mécanique (» Les maths, ça sert à quoi ?). Les similitudes z → az + b, l'application z → z2 sont des transformations conformes, ainsi que toute bijection holomorphe.

Surfaces de Riemann, projection stéréographique et projection de Mercator : »

La mappemonde de Mercator (1587). Source : Nouveau Larousse Illustré, 1905.
Pour un agrandissement, cliquer sur l'Inde nouvelle...

La projection cylindrique de Peters :

Une projection respectant les aires est dite équivalente. C'est le cas (ci-dessous) de la projection cylindrique de Peters (Arno Peters, allemand, 1916-) apparue en 1973.

Dans ce cas le cylindre s'appuie sur les parallèles 45°N et 45°S. Très utilisé aujourd'hui, ce système de projection permet de rendre compte des surfaces effectives des pays et des continents. Le Peters Atlas of the World est apparu en 1989. En France un système assez compliqué de projection équivalente fut autrefois utilisé et mis au point par Rigobert Bonne (1727-1795).


La carte du Monde (planisphère) selon la projection Peters : http://www.petersmap.com

Projection Lambert : »

 ➔   Pour en savoir plus :

  1. Biographie de Mercator sur le site du journal La Libre (Belgique) :
    https://www.lalibre.be/planete/sciences-espace/2011/12/30/mercator-a-mis-le-monde-en-cartes-HS6SYJVH5ZF6JOCDDZUCKQD2JA/

  2. Projection de Mercator, animation sur le site Figures animées pour la physique de Geneviève Tulloue  : 
    https://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Meca/RefTerre/Mercator_FJ.php

  3. Le site éducatif de l'IGN (Institut Géographique National) : http://seig.ensg.ign.fr/

  4. Le site de Thierry Hatt, Lycée Fustel de Coulanges (Acad. Stasbourg) : http://thierry.hatt.gps.free.fr

  5. Cartographie (pour les pros...) : https://desktop.arcgis.com/fr/arcmap/10.3/main/map/mapping-and-visualization-in-arcgis-for-desktop.htm

  6. a) Projection Hammer :
    a) https://en.wikipedia.org/wiki/Hammer_projection
    b) https://pro.arcgis.com/fr/pro-app/latest/help/mapping/properties/hammer.htm

  7. Liste des différentes projections cartographiques : https://fr.wikipedia.org/wiki/Liste_de_projections_cartographiques

  8. Transformations conformes : cours d'analyse, par Jacques Harthong, ENS de Physique de Strasbourg :
    https://cel.archives-ouvertes.fr/cel-00519301v1/document

Tartaglia  Peletier
© Serge Mehl - www.chronomath.com