ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 LAPLACE Pierre Simon,
marquis de-,
français, 1749-1827 |
Savant
universel, astronome, physicien,
mathématicien et fin politicien, Laplace fut inspecteur des
armées avant la révolution de 1789, ministre de l'intérieur sous
Bonaparte,
comte sous Napoléon,
marquis sous Louis XVIII. Il fut ami du chimiste Lavoisier qui
traversa avec moins de chance cette période trouble de
l'histoire de France.
Laplace, brillant jeune mathématicien, fut recommandé par d'Alembert et nommé professeur de mathématiques à l'École Militaire de Paris. Il n'a que 19 ans... Il succédera à Bézout (1784) comme examinateur. Il prouve (1783), en démontrant l'invariance des grands axes des orbites planétaires, la stabilité mécanique du système solaire, ce qui lui vaut, à 24 ans, une place à l'Académie des Sciences.
Examinateur (1785) du jeune Napoléon Bonaparte, alors élève de l'École Militaire, Laplace enseignera ensuite à l'École Polytechnique, dont il fut, avec Monge, un des fondateurs (ainsi que de l'École Normale) avant d'entamer sa carrière politique (sénateur). La Restauration lui valut le titre de Marquis et de pair de France.
Laplace se distingua dans toutes les branches actives de la
science de son époque : électromagnétisme (lois de Laplace
régissant les interactions d'un champ magnétique sur un courant), optique, étude
des gaz, pression atmosphérique, théorie des marées, cosmogonie (théorie de la formation de
l'univers) dans
son Exposition du système du monde (1796,
»
réf.1) où il
expose la genèse de notre monde dans une théorie proche
de celle décrite aujourd'hui.
Son chef d'œuvre est sans doute son traité de Mécanique céleste (5 volumes édités entre 1799 et 1825) où il établit une synthèse magistrale du système solaire basée sur la gravitation universelle de Newton. Ce traité est également consultable sur Google Livres (» réf.4).
i Lors d'une entrevue avec Napoléon Ier, ce dernier le félicite de sa Mécanique céleste tout en lui reprochant, plaisamment : « Mais où est Dieu dans tout cela ? ». Laplace aurait répondu « Sire, je n'ai pas eu besoin de cette hypothèse... ».
Autre contribution remarquable, ses travaux en calcul des probabilités (Théorie analytique des probabilités, 1812, » réf.3) où apparait la méthode de la variation de la constante pour la résolution des équations différentielles.
| Loi de Laplace-Gauss, dite loi normale ou encore distribution gaussienne (1812) : |
Introduite en astronomie par Laplace et Gauss dans le cadre de la théorie des erreurs d'observation, cette loi de probabilité intervient dans l'étude de variables aléatoires continues fondée sur des phénomènes quantitatifs soumis à de multiples causes (aucune d'entre elles n'étant prépondérante), agissant additivement et indépendamment l'une de l'autre et dont la répartition des valeurs s'étale autour de leur moyenne. Elle s'interprète comme loi limite de certains phénomènes discrets.
➔ Par continu, on entend dont les valeurs peuvent être des nombres réels quelconques. Un phénomène non continu est dit discret : ses valeurs sont en nombre fini ou dénombrable, c'est le cas de la loi de Poisson.
loi discrète : » loi continue : »
Revenons à la loi de Laplace-Gauss : il s'agit de la loi de probabilité continue de moyenne m, d'écart-type σ dont la densité f est définie par :
Si X désigne la variable aléatoire suivant cette loi, la transformation affine X → (X - m)/σ permet de se ramener à une loi de moyenne nulle, d'écart-type 1, loi normale proprement dite, ainsi dénommée par Pearson. Pour tout réel t, sa densité vérifie :
Sa fonction de répartition, généralement notée π, s'écrit :
La courbe représentative de f est en forme de "chapeau napoléonien" ou encore, en forme de "cloche", la célèbre cloche de Gauss :
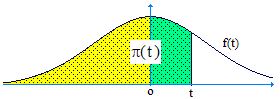
Étude de la loi normale, calcul de π(t), programme JavaScript : »
| Théorème de Moivre-Laplace ou théorème central-limite : |
Ce
théorème est appelé aujourd'hui
théorème central-limite ou
théorème limite central ou
encore théorème de la limite centrale.
Le nom usuel a priori bizarre de central limite (central car la
variable est centrée, limite car on passe à la limite...) est dû
à l'appellation anglaise : central limite theorem, dû à
Polya
qui le démontra dans sa généralité
(1920).
Le résultat énoncé ci-dessous fut approché par de Moivre dans le cas de lois binomiales (dans le vocabulaire de son époque). Il connut de nombreuses variantes et généralisations. Sa forme la plus simple est la suivante :
Considérons n variables aléatoires indépendantes X1, X2 , ..., Xn suivant une même loi de probabilité d'espérance mathématique m, d'écart-type σ et posons Yn = ΣXi/n (moyenne des Xi). Dans ces conditions, E(Yn) = m (espérance) et V(Yn) = σ2/n (variance, carré de l'écart-type). La variable centrée réduite de Yn est alors :
Le théorème central limite énonce que, lorsque n devient infini, Zn converge en loi vers la loi normale centrée réduite, célèbre loi continue de probabilité dont la densité f est :
! Ce n'est pas ici une convergence de suite au sens mathématique usuel :
Convergence en loi :
La notion de convergence en loi exprime une convergence en termes de fonction de répartition. Plus précisément, si l'on pose :
Δn(t) = Pr(Zn < t) - π(t)
où π désigne la fonction de répartition de la loi normale centrée réduite alors la suite des fonctions Δn converge uniformément vers 0 (fonction nulle) sur R.
| Première loi des erreurs proposée par Laplace (1774) : |
Dans la recherche d'une loi de probabilités adaptée à l'estimation des erreurs d'observations, Laplace avait estimé pertinente en première approche, la loi de densité t →½ke-k| t | (- ∞ ≤ t ≤ + ∞).
On vérifie facilement que cette fonction continue est intégrable sur R et que son intégrale est 1 :
| Équation de Laplace, laplacien, fonctions harmoniques : |
L'équation de Laplace est une équation aux dérivées partielles (on parlait à l'époque de différences partielles). Une telle équation a pour inconnue une fonction, intervenant au moyen de ses dérivées partielles par rapport à l'une au moins de ses variables. Laplace introduit le sujet dans ses premiers mémoires de mécanique céleste dès 1782 (Théorie des attractions des sphéroïdes et de la figure des planètes). Dans le texte d'origine, V est ainsi défini, il s'agit de ce que l'on appellera le potentiel gravitationnel du sphéroïde :
➔ L'usage des ∂ ("d rond") pour les dérivées partielles n'est pas le fait de Laplace mais de l'Académie des sciences qui édita ses Œuvres complètes en 10 tomes entre 1878 et 1922 (» réf.3). Legendre adopta cette notation dès 1786, laquelle apparaissait ça et là en Europe mais de façon alambiquée. Elle ne se généralisa lentement qu'à la fin du 19è siècle. Laplace utilisait les notations différentielles usuelles df/dx, df/dy, d2f/dx2. Euler utilisa les notations parenthésées du type (df/dx), (d2f/dx2), ..., peu pratiques et sujettes à confusion.
En savoir plus sur les équations aux dérivées partielles : » Notion de potentiel : »
Laplacien et fonctions harmoniques :
Pour une fonction U de trois variables x, y et z, de classe C2, c'est à dire admettant des dérivées partielles première et seconde continues sur un ouvert Ω de R3, son laplacien est l'opérateur différentiel linéaire souvent noté Δ s'écrivant :
»
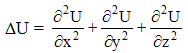différentiation d'une fonction de
plusieurs variables
» Maxwell
On peut généraliser cet opérateur à n variables et aux fonctions de classe C2 sur un ouvert O de Rn. Les solutions de l'équation :
ΔU = 0,
appelée équation de Laplace, sont dites harmoniques sur O. De telles fonctions U s'avèrent analytiques (développables en séries entières, » Condorcet).
Un
exemple
important :
Soit P et Q deux fonctions numériques définies sur un ouvert de O de R2
et posons f = P + iQ. Si f est holomorphe
(dérivable) et de classe C2
au moins, les
conditions de Cauchy montrent que P et Q sont
harmoniques sur O (et toute fonction
holomorphe est analytique).
» Cauchy , Poisson Harmonicité dans le cas du potentiel newtonien : »
On peut énoncer que :
Les partie réelle et imaginaire d'une fonction holomorphe sont harmoniques
L'étude des solutions harmoniques de l'équation de Laplace constituent la théorie du potentiel, issue de la gravitation universelle de Newton. La célèbre équation intervient également en électricité, en théorie de la chaleur (» Fourier), en théorie de l'asservissement : étude d'équations aux dérivées partielles.
En dimension 2, le problème s'insère dans la théorie des fonctions de variable complexe (U fonction de 2 variables x et y) et en dimension 3 le problème est beaucoup plus... complexe (» réf.3).
Valeur moyenne d'une fonction harmonique, fonctions sous-harmoniques : » Dalembertien : »
| Transformation de Laplace : |
En savoir plus sur la transformation de Laplace : »
| La méthode de la variation de la constante : |
C'est à Laplace que l'on doit, dès 1812 dans son Traité analytique des probabilités, la célèbre méthode de la variation de la constante utilisée, dans la résolution des équations différentielles linéaires, pour la recherche d'une solution particulière à partir de la solution générale de l'équation sans second membre (équation homogène).
| Autres travaux : |
Manipulant des tableaux numériques, Laplace annonce la notion de matrice, et étudiera les déterminants des systèmes d'équations linéaires en énonçant la technique de calcul au moyen des mineurs (1772).
Ancienne gare Laplace à Arcueil-Cachan où
vécut l'illustre savant.
Démolie et reconstruite, c'est aujourd'hui une moderne station RER
➔ Pour en savoir plus :
Exposition du système du Monde par Pierre
Simon de Laplace, sur Google Livres :
http://books.google.fr/books?id=mxAOAAAAQAAJ
Essai philosophique sur les probabilités par
Pierre Simon de Laplace sur Google livres :
http://books.google.fr/books?id=kquzFVmtQ04C
Théorie analytique des probabilités par Pierre
Simon de Laplace (1812), sur Google Livres
https://books.google.fr/books?id=BkTVqwQW6loC
Traité de mécanique céleste par Pierre Simon
de Laplace (Éd. 1825) sur Google Livres :
https://books.google.fr/books?id=_A8OAAAAQAAJ
Œuvres complètes de Pierre-Simon Laplace sur le site de
la BnF :
http://gallica.bnf.fr/services/engine/search/sru?operation=searchRetrieve&version=1.2...
L'Huillier
