ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 ARGAND Jean Robert,
français, 1768-1822» La notion implicite de vecteur chez Argand (et Wessel) |
Suisse d'origine, juge et comptable à Genève, ce
mathématicien amateur s'installera libraire à Paris et sera le
premier, avec Wessel
(arpenteur et
géomètre danois, 1745-1818), à interpréter
géométriquement les nombres imaginaires (qualifiés ultérieurement de
complexes par Gauss) et les opérations s'y rattachant :
représentation, addition, multiplication. Mais son mémoire resta méconnu
près d'un siècle !
Argand reprend les mêmes idées que Wessel dans son Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques (1806) la même année que l'abbé Buée. Là encore, cet essai n'est guère pris en compte. Argand l'envoie à Legendre (1813) mais cet auteur inconnu laisse le grand mathématicien sceptique... Pourtant, cette année là, Français et Gergonne s'intéressent au sujet sans s'y attarder.
Ce seront Gauss (à qui l'on devra, en 1831, le qualificatif de complexe pour les nombres imaginaires) et Cauchy, 25 ans plus tard, qui adopteront définitivement ce point de vue et compléteront ses travaux. On doit aussi à Argand, dans ce même ouvrage une démonstration du théorème fondamental de l'algèbre que Cauchy emprunta subrepticement...
➔ Il est très étonnant que l'idée d'une représentation géométrique des nombres complexes laissa récalcitrants tant de mathématiciens européens de haut niveau d'autant que Wallis en 1685 en avait été le pionnier dans son Traité d'Algèbre, De Algebra tractacus !
|
Plan complexe ou diagramme d'Argand ou plan d'Argand-Cauchy : |
Également appelé plan d'Argand-Gauss, il s'agit d'un plan euclidien muni du repère orthonormé (O,1,i) où 1 désigne le vecteur de coordonnées (1,0) et i le célèbre nombre imaginaire de coordonnées (0,1) dont le carré est -1. » notation des vecteurs
Dans son Essai, Argand, tout comme Wessel, interprète √-1 comme une rotation de 90° de l'unité positive autour d'un point origine O. La notation i pour √-1 n'est pas encore utilisée malgré son utilisation par Euler dès 1777.
| Des notations et appellations fondamentales : |
Dans ses notations, la vision d'Argand est clairement vectorielle : il distingue entre OA (longueur, nombre positif) et OA, "lignes dirigées", notation des mesures algébriques d'aujourd'hui. OB est l'opposé de OA.
Réservée aujourd'hui pour les mesures algébriques d'un segment sur un axe, comme AB = xB - xA, cette notation surlignée fut également utilisée antérieurement par Carnot.
Pour Argand, la notation OU désignait le nombre cosθ + √-1.sinθ où θ désigne l'angle que fait OU avec l'unité positive notée 1 (vectoriellement, on écrirait cosθ.1 + √-1.sinθ.i) et OM désigne alors le nombre complexe z = r(cosθ + √-1.sinθ) en posant r = OM.
➔ En termes de coordonnées polaires, on a M(r,θ) et sur l'axe polaire [OM), ON est l'opposé de OM : on a N(r,θ + π); les nombres complexes d'images M et N sont opposés.
» de Moivre , Lefébure de Fourcy
Module & argument, forme z = r(cosθ+ i.sinθ) :
On doit à Argand le terme module (du latin modulus = mesure) pour exprimer la longueur r = OM. Sur le schéma, A et M ont le même module r.
On passe de l'unité 1 à U par la rotation de centre O d'angle θ, puis de U à M par l'homothétie de rapport r : la transformation qui à 1 associe M s'apparente à une similitude plane directe.
Transformations affines de type z' = az + b : »
Cauchy donnera le nom d'affixe au complexe z représenté par M (nom masculin, du latin affixus, participe passé du verbe affigere = attacher à, fixer à) pour signifier ainsi la bijection z ↔ M. Contrairement à ce que l'on peut lire sur certaines pages du web ou dans certains manuels ce substantif est masculin.
Si zA = xA + iyA est l'affixe d'un point A et zB = xB + iyB celui d'un point B, on constate que zB - zA = (xB - xA) + i(yB - yA) : les parenthèses nous fournissent les coordonnées du vecteur AB : on dit que le nombre complexe zB - zA est l'affixe du vecteur AB. Pour tout point M(x,y) du plan, on remarque que l'affixe du vecteur OM n'est autre que l'affixe z = x + iy de M.
C'est encore Cauchy (1838) qui appellera argument de z l'angle θ = (Ox,OM), terme emprunté au vocabulaire de l'astronomie, mesurant l'angle de la position de la lune sur son orbite compté à partir du point où cette orbite coupe celle de la Terre.
Cet argument est noté généralement arg z et désigne une mesure de l'angle (Ox, OM) à 2kπ près. On appelle argument principal et on note Arg z la mesure de (Ox,OM) comprise entre -π et +π. Plus précisément : -π < Arg z ≤ π.
De nos jours, et en classe Terminale notamment, afin d'éviter des confusions de notation entre le i complexe et le vecteur i, souvent utilisé pour définir un repère (O,i,j) du plan, on note (O,u,v) le repère du plan complexe. Avec cette notation, arg z est une mesure de (u,OM) modulo 2π.
➔ Si z = x + iy = r(cosθ + i.sinθ), le module r de z est généralement noté | z | et on a :
Ce module est une valeur absolue dans l'ensemble C des nombres complexes coïncidant avec celle, usuelle, des nombres réels lorsque z est réel ou imaginaire pur (ce qui justifie partiellement la même notation).
En savoir plus sur la notion de valeur absolue : »
! L'argument du complexe nul z = 0 + 0i, de module r = 0 est indéterminé car quel que soit θ : 0 × (cosθ + i.sinθ) = 0.
Si z = x + iy = r(cosθ + i.sinθ) , alors y/x = tanθ, d'où arg z = atan(y/x) + kπ (» fonction atan, arc tangente). Le signe de x (du signe de cosθ) et le signe de y (du signe de sinθ) permettent de calculer Arg z sans ambigüité.
Arg zz' = Arg z + Arg z mod. 2π
Si z est non nul, Arg 1/z = - Arg z mod. 2π
Si z' est non nul, Arg z/z' = Arg z - Arg z' mod. 2π
∗∗∗
1 â désignant un angle de l'intervalle ]π/2;π],
calculer le module et un argument du nombre complexe z = 1/(1 - i.tan â)
Indications : remarquer que 1 + tan2 â = 1/cos2 â. On a z = cos â(cos â + i.sin â) = -cos â(-cos â - i.sin â) = -cos â[cos (π + â) + i.sin (π + â)].
Le module de z est donc -cos â (positif) et un argument est π + â.
2 On pose u = sin 2â - i(1 + cos 2â), v = (1 - cos 2â) - i.sin 2â et z = u/v , â∈]0;π/4]. Montrer que u/v = 1/tan â
3
z = x + iy et z' = x' + iy' sont deux nombres complexes. Montrer que Re(zz')
≤ |z|.|z'|
Indications : si Re(zz')est négatif, le cas est
trivial, sinon, élever au carré : une identité remarquable devrait apparaître...
4
Soi P un polynôme à coefficients réels admettant z comme zéro, montrer que l'on a aussi P(z) = 0.Autres exercices niveau Terminale et Sup : » d'Alembert et les nombres imaginaires : »
| La notion implicite de vecteur : |
Dans l'addition géométrique des nombres complexes, Argand est amené à poser la formule :
C'est la formule dite de Chasles. Argand annonce ainsi l'entrée en scène de la notion de vecteur : il voit dans les nombres imaginaires (nombres dits complexes depuis Gauss) des lignes dirigées : segments orientés du plan : c'est bien, là encore, le point de vue de Wessel.
Ce concept, déjà présent chez Stevin au 16è siècle, se rencontrera implicitement dans les travaux de Möbius et de Chasles mais principalement et plus formellement avec Bellavitis (dans sa théorie des équipollences) et ses contemporains Hamilton, à qui l'on doit d'ailleurs l'appellation vecteur, et Grassmann. Le calcul vectoriel verra son plein essor avec les travaux novateurs de Gibbs.
semble apparaître sporadiquement à vocation pédagogique, dans les années 1930-1940. Elle n'est pas universelle. On utilise souvent encore de nos jours les caractères gras italiques, c'est le cas dans ChronoMath, car plus simple sur le plan de la typographie et de la mise en page :
AB = AC + CB
| Usage des nombres complexes en géométrie euclidienne plane : |
• Dans le plan complexe rapporté au repère orthonormé (O,u,v), d'axes (Ox) et (Oy), se donner M de coordonnées x et y, d'affixe z = x + iy, souvent noté M(z), c'est se donner le vecteur OM. z est aussi l'affixe de OM et ce dernier vecteur est l'image vectorielle de z.
• Si A est un point d'affixe a et B d'affixe b, alors AB = OB - OA est d'affixe b - a.
• Si OM est l'image vectorielle de z, alors arg z = (Ox, OM) = (u, OM) » Angles orientés de vecteurs et de droites
• Soit A et B des points d'affixes respectifs a et b tels que (u, AB) = θ mod. 2π, on reporte AB en OM. On a OM = OB - OA d' affixe b - a et d'argument θ : (u, AB) = arg (b - a) mod. 2π
• MA = MB (distances) équivaut à écrire : | z - a | = | z - b | : M décrit la médiatrice de [AB].
• Si
u et u' sont les images vectorielles
de z et z', alors :
♦ u et u' sont colinéaires
ssi z'/z réel.
♦
u
orthogonal à u' ssi z'/z imaginaire pur.
♦ (u,u') = arg z'/z mod. 2π
• Si A, B et C sont des points distincts
d'affixes respectifs a, b et c :
♦
A, B et C sont alignés ssi
(c - a)/(b - a) est réel. On peut préférer dire (b - a)/(c - a) réel ou (a -
b)/(a - c) réel, ...
♦
(AB)
⊥ (AC) sont
perpendiculaires ssi (c - a)/(b - a) est imaginaire
pur. Là encore, on peut effectuer quelques permutations judicieuses.
• Si, dans une rotation de centre A(a), d'angle
θ, un
point M(z) a pour image M'(z), alors z' - a = eiθ
x (z - a)
C'est un
cas particulier de similitude directe.
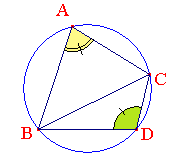
• A, autre que B et C, appartient au cercle de diamètre [BC] ssi arg(c - a) - arg(b - a) = π/2 mod. π.
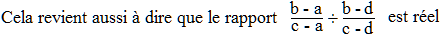
Wessel et les nombres complexes : » Euler et les nombres complexes : »
➔ Pour en savoir plus :
Fourier