ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BOREL Émile Félix
Édouard Justin,
français, 1871-1956
»
Cours Peccot |
»
Source portrait : avec l'aimable
autorisation du Portail de la ville de
Saint-Affrique en Aveyron où l'on trouvera une biographie plus
complète en cliquant sur l'image. Éléments biographique : Ibid, +
CDSB +
Académie des sciences.
On ne confondra pas Émile Borel avec Armand Borel, mathématicien suisse (1923-2003) dont on pourra consulter la biographie et un aperçu de ses travaux : hommage à Armand Borel (par Jean-Pierre Serre).
Né à Saint-Affrique (Aveyron), major de Polytechnique et de l'École Normale Supérieure à 18 ans, la thèse d'Émile Borel, Sur quelques points de la théorie des fonctions, fut dirigée par Darboux (1893). Borel fut un des premiers jeunes mathématiciens à occuper le poste du cours Peccot du Collège de France de 1899 à 1902 (» note). Maître de conférence à Lille la même année, il enseignera ensuite à l'ENS (1897-1920) et à la faculté des sciences de Paris-Sorbonne sur une chaire de théorie des fonctions réelles et complexes (1909-20), puis de probabilités (1920-40).
Directeur scientifique de l'École Normale Supérieure, ami de Paul Appell (dont il épousa une des filles), de Paul Valéry, de Paul Painlevé (mathématicien, ministre puis président du conseil, équivalent à premier ministre ou chef du gouvernement comme on disait à l'époque), Borel fut aussi député de l'Aveyron et ministre de la Marine (1925). Outre ses travaux en mathématiques, Borel étudia les géométries non euclidiennes appliquées à l'espace-temps eu égard à la théorie de la relativité d'Albert Einstein (années 1910).
On lui doit, avec en particulier la participation de Darmois, la création (1922) de l'ISUP (Institut de statistique de l'université de Paris) et, financé en partie par la fondation Rockfeller et le baron de Rothschild avec l'appui de David Bikhoff, ainsi que la création (1928) de l'Institut Henri Poincaré pour la recherche en mathématiques pures et appliquées, dont il fut le directeur pendant 20 ans, aujourd'hui rattaché à l'université Pierre et Marie Curie (UPMC) et au C.N.R.S.
Dirigé par Cédric Villani depuis 2009, l'Institut l'est désormais par Sylvie Benzoni suite à la nouvelle carrière de député LREM (parti La République en marche d'Emmanuel Macron) du médiatique et excentrique mathématicien, plus connu aujourd'hui, hors du monde mathématique, par sa lavallière et sa broche araignée que par ses travaux mathématiques...
Institut Henri Poincaré (site externe) : » ISUP : »
Borel reçut le Grand Prix des sciences mathématiques de l'Académie des sciences (1898) pour son étude relative aux séries divergentes. Élu à ladite Académie (1921), il en sera président en 1934. Membre du Bureau des longitudes (1946), il reçut la première médaille d'or du CNRS (1954). Borel, à l'image de Kronecker, est considéré comme un mathématicien constructiviste.
| Théorie de la mesure, ensembles et applications mesurables, σ-algèbres (tribus) : |
à 28 ans, dans ses Leçons sur la théorie des fonctions (» réf.1), Borel fut à l'origine, avec Jordan, de la théorie de la mesure des ensembles (1897-98) ainsi que de la théorie moderne du calcul des probabilités dans le cadre des σ-algèbres constituant les parties mesurables d'un espace topologique (qualifiées de tribus par Bourbaki) : Traité du calcul des probabilités et de ses applications (éditions publiées de 1925 à 1940). Le concept d'ensemble mesurable sera magistralement développé par Borel et deviendra le fondement de l'analyse mathématique moderne sur lequel s'appuiera Lebesgue pour la mise en place de sa théorie de l'intégrale (1902) : grâce à ce nouvel outil, ce dernier à profondément remanié et généralisé le calcul intégral en créant une théorie de la mesure universelle applicable à toutes les branches des mathématiques.
Mesurer un objet mathématique abstrait est la généralisation des grandeurs issues de l'Antiquité au sens usuel de longueur, aire, volume. Calculer une probabilité, c'est mesurer les "chances" de réalisation d'un événement (en tant que partie d'un ensemble : » Kolmogorov). L'intégrale de Riemann d'une fonction positive mesure concrètement l'aire "sous" la courbe. Le concept de mesure est ainsi étroitement liée à la topologie, au calcul intégral, aux probabilités. Un ensemble abstrait étant donné, il s'agit de définir dans cet ensemble une fonction numérique satisfaisant aux propriétés intuitives de "mensuration", en particulier l'additivité, voire positivité. Mais on ne peut pas mesurer n'importe quoi.
Leçons sur la théorie des fonctions (page 42)
Notions élémentaires de la théorie de la mesure, σ-algèbres, ensembles boréliens : »
Borel est également à l'origine de la théorie des jeux stratégiques et de la cybernétique que développeront les américains Von Neumann, Morgenstern et, en France, Couffignal. Il intervint également en topologie et en théorie des fonctions réelles et complexes (» réf. 1);
| Mesure de Borel-Stieltjes : |
F désignant une fonction numérique, croissante et continue à droite, on peut lui associer une
mesure µ, unique, vérifiantµ(]a,b]) = F(b) - F(a).
Lorsque F admet une limite nulle en - ∞, F est appelée fonction de répartition de µ et si µ s'avère être une probabilité (cf ci-dessus), la limite en +∞ de F est 1.
➔ Lorsque F est l'application identique, on parle de mesure de Borel de la droite réelle et l'on a alors µ(]a,b]) = b - a.
Introduction à l'intégrale de Stieltjes : » Introduction à l'intégrale de Lebesgue : »
| La loi forte des grands nombres : |
Il s'agit là de la première "découverte" de cette loi des grands nombres dite forte, comparativement à la loi faible) exprimée par Borel en 1909 dans son traité Les probabilités dénombrables et leurs applications arithmétiques où il définit le concept de nombre normal :
Soit (Xn) est une suite de variables aléatoires indépendantes, de même loi, d'espérance mathématique finie m, sur un même espace probabilisé. Alors, n tendant vers l'infini, on a :
= m ] =
1. C'est dire que la suite de terme général Yn = (X1 + X2 + ...+ Xn)/n converge vers la constante m presque sûrement.
Rappel :
Une suite (An) d'événements est dite indépendante ou mutuellement indépendante lorsque tout sous-ensemble fini {Ai1, Ai2, ..., Aip} de ces événements constitue une famille d'événements indépendants, autrement dit :
Prob(Ai1∩Ai2∩...∩Aik) = Prob(Ai1) × Prob(Ai2) × ... × Prob(Aik). » Bayes
Une variante de la loi des grands nombres de Bernoulli (dite faible) fut énoncée par Poisson en 1837.
| Théorème (ou lemme) de Borel-Cantelli : |
Ce résultat, exprimé par Borel en 1909 dans ses
Éléments de la théorie des probabilités, fut repris par
Cantelli en 1917 dans une approche plus précise :
Si (An) une suite dénombrable d'événements d'un espace probabilisé, alors :
Si la série ΣProb(An) converge, alors seul un nombre fini des An peuvent se produire simultanément. Autrement dit, l'événement « une infinité d'événements An se produisent simultanément » est impossible (probabilité 0).
Si la série ΣProb(An) diverge (limite +∞) et si les An sont indépendants (» ci-dessus), alors l'événement « une infinité d'événements An se produisent simultanément » est certain (probabilité 1).
» Cantelli , Kolmogorov
| Axiome de Borel-Lebesgue : |
Un espace topologique E vérifie l'axiome de Borel-Lebesgue si de tout recouvrement de E par des ouverts, on peut extraire un recouvrement fini. On dit alors que E est quasi-compact.
Si E est séparé, alors E est compact.» Lebesgue Topologie, différents types de compacité : »
| Théorème de Borel-Lebesgue : |
Dans un espace normé de dimension finie, les parties compactes sont les parties fermées bornées.
| Théorème de Heine-Borel : |
Toute fonction continue sur un intervalle fermé [a,b] est uniformément continue sur [a,b].
» Heine
| Une approximation de π : |
Dans une publication intitulée
Sur l'approximation des
nombres réels par les nombres quadratiques (Bulletin
de la Société Mathématique de France, 1903), Borel
constate que la partie décimale de 8π est "très
voisine" de celle de √229 : leur
différence est en effet de l'ordre de 4,7 x
10-6.
On a donc √229 + 10 ≅ 8π. Ce qui conduit à une valeur approchée du célèbre nombre, à moins de 5 × 10-6 près, au moyen de la formule :
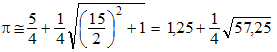
» Le texte
numérisé contient curieusement une erreur : 1/2 au lieu de 1/4 devant le
radical.
| Le concept de nombre normal : |
Dans son mémoire Les probabilités dénombrables et leurs applications arithmétiques, paru en 1909, Borel s'intéresse à la distribution (au sens probabiliste) des chiffres composant un nombre écrit dans une base b et qualifie de nombre normal relativement à la base b, tout nombre x vérifiant la propriété suivante :
où φ(a) désigne le nombre d'occurrences du chiffre a parmi les n premiers chiffres de l'écriture en base b de x. Borel s'attache tout particulièrement à la base b = 2 (nombres dyadiques) et aux nombres réels de l'intervalle [0,1] et démontre que tout nombre réel est normal à l'exception d'un ensemble de nombres de mesure nulle au sens de Lebesgue : les entiers naturels (le nombre de chiffres est fini), les nombres rationnels (leur développement est périodique) et quelques autres sans doute... : la preuve de la normalité du célébrissime π n'est pas établie aujourd'hui (novembre 2009).
Concrètement, en choisissant la base 10, donc l'écriture usuelle avec nos chiffres 0 à 9, dits arabes, considérons le nombre π :
Pour n grand, la proportion de 0, de 1, de 2, ... de 9 dans les n premiers chiffres semble la même et de l'ordre de 10% (1/b = 1/10). On peut facilement vérifier ce résultat au moyen des ordinateurs : π semble normal. Ouff !..
En admettant que la présence consécutive d'un chiffre c et d'un chiffre c' sont des événements indépendants, il vient que, pour un nombre normal, la proportion de 00, 01, ... 99 dans les n premiers chiffres est la même et de l'ordre de 1/10 × 1/10, soit 1%. De même pour les séquences de 3 chiffres consécutifs : 1‰ (1 pour mille).
On voit sur la dernière ligne de l'approximation de π ci-dessus la présence de six 9 consécutifs : si π est normal, comme on le pense, cette occurrence a autant de chances de se produire que les autres : à savoir 1 chance sur 1 000 000 dans l'écriture de π. A noter que la normalité d'un nombre dans une base n'assure pas sa normalité dans une autre !
Définition et théorème de Borel :
Borel qualifie d'absolument normal, un nombre réel normal relativement à toute base. Il prouve qu'un nombre absolument normal est irrationnel et que :
Presque tous les nombres réels sont absolument normaux
» Presque tous signifiant à l'exception d'un ensemble négligeable, c'est à dire de mesure de Lebesgue nulle.
i Les nombres normaux furent ultérieurement étudiés tout particulièrement par le statisticien anglais David G. Champernowne, professeur à Cambridge (1912-2000) qui nous a légué (1933) un nombre normal portant son nom :
0,123456789101112131415161718192021222324252627...
Vous avez certainement compris l'algorithme de fabrication de ce nombre également transcendant. On ne sait pas si ce nombre est absolument normal.
» Feynman , Mendès-France
Cours et prix Peccot du Collège de France :
La Fondation Claude-Antoine Peccot du Collège de France fut créée en 1885, avec le soutien de Joseph Bertrand, sur des fonds privés de la famille de Claude-Antoine Peccot (1856-1876), un jeune et brillant étudiant, licencié es-sciences à 19 ans, mort brutalement à l'âge de 20 ans alors qu'il poursuivait ses études de mathématiques à la Sorbonne. La fondation, toujours active, octroie depuis sa création des bourses d'études et un prix annuel.
Le cours Peccot du Collège de France, issu de la fondation, est un poste honorifique (éventuellement reconductible) attribué chaque année depuis 1900 à de jeunes mathématicien(ne)s prometteurs (1 à 3), âgés de moins de 30 ans, enseignant généralement dans le prolongement de leur thèse de doctorat. (» réf. 14).
➔ Pour en savoir plus :
Éléments de Mathématique, Topologie générale, Ch. 1, §9 - N. Bourbaki, Éd. Hermann, Paris - 1965
Nombres normaux et fonctions pseudo-aléatoires, par
M. Mendès-France
http://archive.numdam.org/article/AIF_1963__13_2_91_0.pdf
a) Le prix Peccot sur le site de la SMF (» page 57) :
http://smf4.emath.fr/Publications/Gazette/2011/129/smf_gazette_129_51-68.pdf
b) Liste chronologique des cours Peccot sur le site du Collège de France :
https://www.college-de-france.fr/media/cours-peccot/UPL1466994975427365342_..._.pdf
Enriques