
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|

A l'origine, la géométrie est la mesure de la Terre : en grec, gê = terre et metron = mesure. En premier lieu, Euclide définit les objets usuels de la géométrie plane :
point : ce dont la partie est nulle;
ligne (finie) : longueur sans largeur dont les extrémités sont des points;
droite : ligne qui est également (de manière égale) placée entre ses points;
droites (distinctes) parallèles d'un même plan : droites qui, prolongées indéfiniment d'un côté ou de l'autre, ne se rencontrent pas.
» Euclide ne définit pas le segment par un terme spécifique : il parle de droite finie (limitée de part et d'autre). On note d // d' pour exprimer que les droites d et d' sont parallèles et, dans la pratique, on utilisera la définition : d // d' si et seulement si : d = d' ou bien d et d' ne se rencontrent pas (n'ont aucun point en commun).
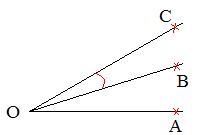
angle : inclinaison mutuelle (de l'une par rapport à l'autre) de deux droites n'ayant pas
même direction;
→
une définition
pas évidente, voir figure : la demi-droite [OB) a une certaine inclinaison par
rapport à [OA) choisie ici "horizontale". Si on prend maintenant [OB) comme
demi-droite de référence, [OC) a une inclinaison : la même que [OB) par
rapport à [OC) : c'est l'inclinaison mutuelle.
droites perpendiculaires : lorsqu'une droite tombe sur une autre en formant des angles tels que deux quelconques d'entre eux aient même mesure (superposables), on dit que les droites sont perpendiculaires et que les angles formés sont droits;
surface : est ce qui a seulement longueur et largeur;
plan : surface également placée entre ses droites;
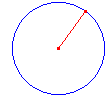
cercle : figure plane constituée d'une seule ligne telle que tous les segments (rayons du cercle) que l'on peut lui mener depuis un point ont même longueur; ce point est le centre du cercle;
polygones : ligne brisée fermée (du grec poly = plusieurs et gônia = angle) dont le triangle (3 angles) est l'exemple le plus élémentaire. On distingue le triangle isocèle (2 côtés de même mesure), le triangle équilatéral (3 côtés de même mesure), le triangle scalène (trois côtés inégaux (du grec skalenos = oblique), le triangle rectangle (possédant un angle droit). On remarque qu'un polygone possède autant d'angles que de côtés.
Pour 4 côtés, on parle de quadrilatère (du latin quadrilatérus : quatre côtés) plutôt que de tétragone (du grec quatre angles). Puis le grec l'emporte : pentagone (5 côtés), hexagone (6 côtés), heptagone (7 côtés), etc.
En savoir plus sur les polygones : »
➔ Notons là encore (» Platon) que les objets visibles qui résultent de ces définitions (figures) ne sont que des représentations imparfaites de ces concepts mathématiques que nul ne peut en fait contempler si ce n'est par la pensée.
Les figures aident à développer un raisonnement conduisant à extraire des propriétés dans un contexte complexe mais elles peuvent devenir trompeuses si l'on s'attache à des faux-semblants résultant de leurs tracés nécessairement imparfaits. Écueil classique des élèves...
|
|
∗∗∗
•
Angles & mesures en degrés (niveau 6ème, 3
exercices)
niveau 6ème |
|
Les célèbres postulats de la géométrie d'Euclide : » distinguo axiome/postulat |
Après les définitions, Euclide pose ensuite ses fameux postulats (ses demandes) dont le cinquième est resté LE postulat d'Euclide, souvent dit axiome (ou postulat) des parallèles et qui fut sujet à nombreuses recherches et controverses quant à sa nécessité :
1. Étant
donnés deux points A et B, il existe une droite passant par
A et B;
Euclide écrit : Conduire une droite d'un point quelconque à un point
quelconque.
2. Tout segment
[AB] est prolongeable en une droite passant par A et B;
3. Pour tout point A et tout point B distinct de A, on peut décrire un cercle de centre A passant par B;
4. Tous les angles droits sont égaux entre eux;
5. Par un point
extérieur à une droite, on peut mener une
parallèle et une seule à cette droite.
»
Si une droite, tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.
C'est quoi M'sieur un axiome d'incidence ?
On parle souvent d'axiomes d'incidence pour parler des postulats 1, 3 et 5 ci-dessus. Le mot incidence provient du latin incidere signifiant tomber sur. En physique on parle par exemple d'un rayon incident tombant sur une surface; en termes de réflexion sur un miroir, on parle d'angle incident et d'angle réfléchi. Dans son axiome 5, ci-dessus, Euclide nous dit Si une droite, tombant sur deux droites, fait... : parler en classe d'axiomes d'incidence, pourquoi pas, mais il s'agira d'en préciser le sens... dans le sens indiqué !
Immédiatement après les postulats et définitions, débutent les premières propositions fondamentales qui permettront à Euclide d'apporter la preuve d'assertions plus difficiles. Par exemple :
| L'émergence de géométries non euclidiennes : |
Du 9è au 19è siècle, nombreux furent les mathématiciens arabes et européens qui ont cherché à démontrer le 5è postulat à partir des quatre premiers. Sans succès. En fait, ils utilisaient alors inconsciemment dans leurs démonstrations une assertion équivalente ! Malgré l'apport des travaux de Saccheri, le français Legendre, par exemple, s'est acharné pendant près de 40 ans à prouver que la somme des angles d'un triangle est égale à deux angles droits sans usage du 5è postulat dans le but d'en déduire ce dernier.
Le 5è postulat fut ainsi sujet à d'innombrables études mais n'a jamais été remis en cause quant à sa compatibilité vis à vis des quatre premiers : le système axiomatique d'Euclide n'est pas contradictoire. Afin de montrer qu'un système d'axiomes n'engendre pas de contradictions, il suffit d'exhiber une proposition toujours vraie (tautologie au sens logique : vraie quels que soient les variables qui la composent) résultant de l'ensemble des axiomes.
➔ Le problème fut également de savoir si le 5ème axiome était dépendant des autres. Dans l'affirmative, il serait démontrable au moyen des autres et deviendrait un théorème du système. Les travaux des géomètres consistèrent tout d'abord à le remplacer par sa négation : cela n'engendra aucune contradiction, montrant que le fameux postulat était indépendant des autres et finalement indispensable à la géométrie euclidienne plane et de l'espace... euclidien. Toutes ces recherches et ces échecs menèrent finalement à la découverte de nouvelles géométries dites non euclidiennes :
♦ Si on le retire au profit de l'affirmation que deux droites distinctes sont sécantes à l'infini, c'est la géométrie projective (on ajoute au plan des points dits à l'infini, assimilés aux directions de droites, constituant la ligne de l'infini : Desargues, Poncelet.
♦ Si on le remplace par l'impossibilité, au contraire, de tracer une parallèle à une droite, on obtient la géométrie elliptique : par exemple, la géométrie de la sphère (surface à courbure constante positive) : Gauss, Klein, Riemann.
♦ Enfin, si on pose maintenant que par un point extérieur à une droite on peut mener une infinité de parallèles à cette droite, on obtient la géométrie hyperbolique, dite aussi de Lobatchevski, dont une représentation est la géométrie de la pseudosphère (surface à courbure constante négative) : Lobatchevski, Poincaré, Beltrami.
» Oswald Veblen Les géométries non euclidiennes : »
| Un sixième postulat..., cas d'égalité des triangles, triangles semblables : |
On trouve, dans certaines éditions des Éléments, un 6è postulat selon lequel deux droites ne peuvent enfermer un espace. Selon l'historien des mathématiques arabes, A. P. Youschkevitch, il serait un ajout, sans doute des mathématiciens arabes, comme Ibn al Haytham et Al Khayyam, lors de leurs commentaires des Éléments afin d'établir plus rigoureusement la proposition 4 du livre I des Éléments énonçant le premier cas d'égalité des triangles :
Si deux triangles ont un angle égal, compris entre deux côtés égaux "chacun à chacun",
alors ces deux triangles sont égaux (superposables)
L'expression "chacun à chacun", aujourd'hui désuète, signifiait "respectivement". Le 1er cas d'égalité peut s'exprimer ainsi (selon les générations de manuels scolaires, les premier et second cas peuvent s'interchanger :
Si deux triangles ont un angle égal,
compris entre deux côtés respectivement égaux,
alors ces deux triangles sont égaux (superposables)
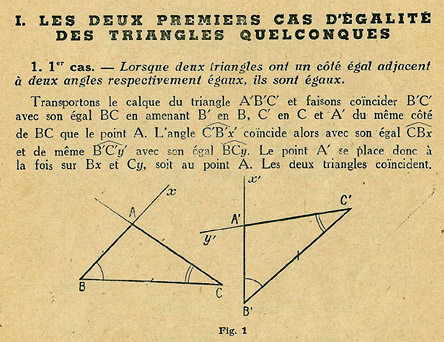
Dans cette figure, les angles ^ABC et ^A'B'C'
et les côtés [AB] et [A'B'] sont homologues
➔
Par triangles égaux, on entendait jusque dans les années 1950-60, des triangles ayant leurs six éléments correspondants de mêmes mesures (angles et côtés). Ces éléments correspondants portent aussi le qualificatif d'éléments homologues.Ci-dessus : Formulation et "preuve" (on peut déplorer le manque de rigueur dû à l'usage d'un calque, mais n'ergotons pas...), du 1er cas d'égalité des triangles, extraite du manuel Lebossé-Hémery, Algèbre, Arithmétique et Géométrie, classe de 4ème des lycées et collèges, Ed. Nathan, 1951.
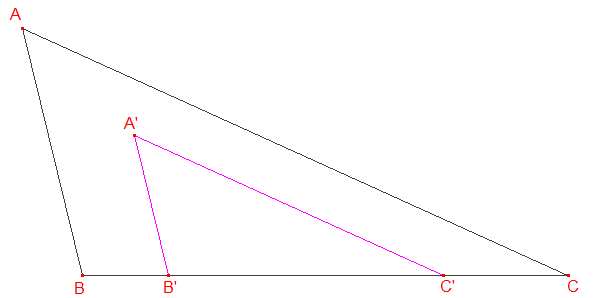
! Bien noter que deux triangles ayant des angles de même mesure ne sont généralement pas égaux. Le cas des triangles équilatéraux en est un exemple. Voici un autre cas :
Rappelons les second et troisième cas :
2/ Si deux triangles ont un côté égal, compris entre deux angles respectivement égaux, alors ces deux triangles sont égaux.
3/ Si deux triangles ont leurs trois côtés respectivement égaux, ces deux triangles sont égaux.
Ces résultats montrent que trois données correspondant (ou se ramenant) à ces trois cas conduisent à la construction d'un triangle et un seul. Par exemple, si AB = 6, ^ABC = 55° et ^ACB = 65°, on déduit ^CAB = 180° - 55° - 65° = 60° et l'application du second cas conduit à l'unicité du triangle ABC et à sa construction.
∗∗∗
Niveau 3è : Dans un
triangle ABC, on suppose connu BC et les angles ^B et ^C.
Prouver, en traçant la hauteur issue de A et en distinguant les deux cas ^B aigu
et ^B obtus que :

Niveau lycée :
Retrouver ce résultat en utilisant la
formule des sinus
∗∗∗
Résolutions de
triangles ,
Parallèles équidistantes
Euclide étudie aussi les relations entre les côtés de triangles dont les angles ont les mêmes mesures, sans condition de parallélisme sur les côtés, ce qui le conduit à établir des relations de proportionnalité analogues à celles rencontrés dans la propriété de Thalès. Il s'agit des triangles semblables dont on trouvera de nombreuses applications dans ChronoMath :
Somme des angles d'un triangle : » Inégalités dans le triangle : » Triangles semblables : »
| Raisonner, démontrer, prouver, déduire, CQFD : |
L'art du raisonnement hypothético-déductif consiste, à partir de postulats ou résultats déjà acquis et donc posés comme hypothèses (au sens premier : assertions, propositions sous-jacentes supposées vraies), en la déduction (conséquence) logique de nouveaux résultats.
Par logique, on entend étymologiquement un discours (du grec logos = discours et logikê = qui est relatif à la raison) objectif s'appuyant exclusivement sur les hypothèses. Euclide et Aristote ont élevé le raisonnement hypothético-déductif au plus haut niveau de la pensée scientifique et philosophique de leur époque.
La méthode de démonstration dite de réduction à l'absurde (ou raisonnement par l'absurde), initiée par Aristote fut un puissant outil utilisé par Euclide.
![]()
Déraisonner,
c'est ne pas avoir un discours logique. De méchants et irrespectueux professeurs
disent parfois d'un élève
qu'il résonne comme un
tambour (le tambour, comme chacun sait, est vide). Une tête bien
pleine ne résonne pas, elle raisonne !

Aristote, le syllogisme et la dialectique : »
➔ Le célèbre CQFD, Ce Qu'il Fallait Démontrer, est la traduction française du QED, Quod Erat Demonstrandum, acronyme latin traduit de l'équivalent grec qu'utilisait systématiquement Euclide pour clore une démonstration.
Preuve, selon Euclide, du théorème de Pythagore :
» et du théorème d'Al Kashi : »
∗∗∗
Apprendre à démontrer
»
Apprendre a construire ,
Exercices
élémentaires sur les angles , Voir
aussi...
|
Quadrilatères
& triangles particuliers
|
Caractériser un losange
#2
|
|
Caractérisation d'un
carré #1
|
A la découverte d'un
losange
|
|
Caractérisation d'un
carré #2
|
Sans titre !
|
|
Caractérisation d'un
carré #3
|
Un quadrilatère un peu
particulier... |
|
Caractérisation d'un
carré #4
|
Une application de
l'inégalité triangulaire
|
|
Losange & parallélogramme
|
Construire,
conjecturer, démontrer |
|
Caractériser un losange
#1
|
C'est évident
|
 |
Cette page, comme toutes celles de ChronoMath, représente un travail personnel non négligeable de recherches. A ceux qui l'ont recopiée et publiée sur leur site ou blog sans pudeur ni scrupule (ou qui s'apprêteraient à commettre cette abomination...) , je recommande de vérifier les informations qu'elle contient car elles peuvent être entachées d'erreurs (y compris d'orthographe !) et de s'interroger sur les problèmes de déontologie, de bonne éducation et de droits d'auteur... |
| Qu'est-ce qu'une construction mathématique au sens d'Euclide ? |
 Construire une figure consiste,
sauf consigne contraire, à déterminer les points qui la
constituent en utilisant ces deux seuls instruments, la règle
et le compas, hérités de la tradition
platonicienne
:
Construire une figure consiste,
sauf consigne contraire, à déterminer les points qui la
constituent en utilisant ces deux seuls instruments, la règle
et le compas, hérités de la tradition
platonicienne
:
♦ La règle est considérée ici comme un moyen de relier deux points (déjà construits) : elle sert à tracer un segment ou une droite; elle n'est donc pas graduée. La règle permet aussi de construire un point en tant qu'intersection de deux lignes (une ligne est ici une droite, un segment, un cercle ou une courbe quelconque déjà construits).
♦ Le compas sert à tracer des cercles dont le centre et un point (ou le rayon : écart) sont déjà déterminés. Le compas permet également de construire un point en tant qu'intersection de deux cercles.
L'usage des règle et compas seuls dans une construction oblige à la réflexion, au raisonnement, mais il ne doit pas être obligatoire ou systématique (à l'école ou au collège).
On remarque chez les jeunes élèves (6è, 5è) la difficulté à se forger une image mentale a priori d'une figure géométrique, même élémentaire comme un segment en tant que côté d'un triangle : pour de nombreux enfants, deux arcs de cercles centrés en A et B et se coupant en C est un dessin, et non une figure géométrique structurée, possédant des propriétés.
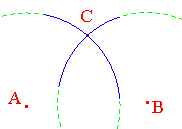
La présence implicite des segments [AC] et [BC] (rayons) n'est pas perçue. D'où la difficulté pour ces élèves à construire des objets géométriques sans l'usage de la règle graduée : si les mesures ne leur sont pas données, la figure est "impossible", le professeur a "oublié de donner les mesures"...
à l'école, si l'objectif de la construction est d'évaluer les connaissances de l'élève sur un nouveau savoir et les propriétés géométriques remarquables de ce savoir (par exemple, construire la médiatrice d'un segment, suite à sa caractérisation), on pourra exiger l'usage des seuls règle non graduée et compas. Sinon on parlera de tracer plutôt que de construire. Et là, tous les outils sont permis.
L'usage d'une règle graduée, d'un rapporteur, d'une équerre (du latin, préfixe é : augmenter et quadrare = rendre droit, qui a aussi donner équarrir), d'une bande de papier, voire d'une calculatrice, apparaîtra généralement dans les cas où la construction d'une figure n'est qu'un support visuel du problème étudié et non un objectif.
∗∗∗
Apprendre à Construire
Le dogme de la règle et du compas : un frein dans le développement mathématique ?
 L'admiration quasi mystique de la droite et du
cercle induite par Platon,
induisant la notion de construction géométrique acceptable à l'aide du compas
et de la règle seuls, a pu être un frein au développement des mathématiques
par le biais de la géométrie euclidienne.
L'admiration quasi mystique de la droite et du
cercle induite par Platon,
induisant la notion de construction géométrique acceptable à l'aide du compas
et de la règle seuls, a pu être un frein au développement des mathématiques
par le biais de la géométrie euclidienne.
En effet, l'intersection d'une droite et d'un cercle fournit au plus deux points : la conséquence de ce dogme de la construction et d'une mathématique reposant sur la géométrie est une algèbre limitée aux équations des premier et second degré ne fournissant des solutions qu'à des problèmes au plus quadratiques (du second degré), donc constructibles. Ainsi, hormis les coniques, il est illusoire de rechercher l'intersection d'une courbe et d'une droite au moyen de la règle et du compas ! Tout aussi impossible est le problème du tracé à la règle et au compas d'une (ou des) tangente(s) à une courbe donnée lorsque cette courbe n'est pas une conique.

Euclide
(ou Archimède selon certains)
L'École
d'Athènes, selon Raphaël- Détail ,
Chambre
de la Signature,
Vatican
Conscients cependant des limites de la règle et du compas, les mathématiciens grecs débordèrent d'imagination et de génie dans leur acharnement à résoudre les subtils problèmes que furent la duplication du cube, l'évaluation de π, la trisection de l'angle ou la quadrature du cercle.
L'étude des sections coniques, l'invention de courbes ingénieuses comme la conchoïde de droite et la théorie des proportions, permirent d'aborder des problèmes relevant du 3ème ou 4ème degré.
Section dorée et pentagone/décagone régulier : »
|
Inégalités usuelles dans le triangle : |
Certains problèmes métriques de géométrie demandent quelques connaissances des relations élémentaires liant les côtés aux angles du triangle et permettant de comparer ces côtés et ces angles. Euclide se pencha sur le sujet.
La plus connue est l'inégalité triangulaire
(» i4 ci-après), utilisée dans la définition d'une distance d'un espace métrique, et enseignée dès le collège en classe de 5ème. Voici l'ensemble des inégalités usuelles du triangle :♦ I1/ (Euclide, Livre I, XVI) : la mesure d'un angle extérieur est supérieure à chacune des mesures des deux angles intérieurs non adjacents et, plus précisément, sa mesure est la somme des mesures des angles non adjacents.
Angles adjacents :
Rappelons que par angles adjacents, on entend deux angles ayant un côté commun et dont les autres côtés sont situés de part et d'autre de ce côté commun. Ci-dessus, ^BCA et ^ACD sont adjacents. Il en est de même de ^ACD à ^xCD mais ^BCA n'est pas adjacent à ^xCD.
Ci-dessous, l'angle extérieur ^xCA égale (en mesure) ^CBA + ^BAC :
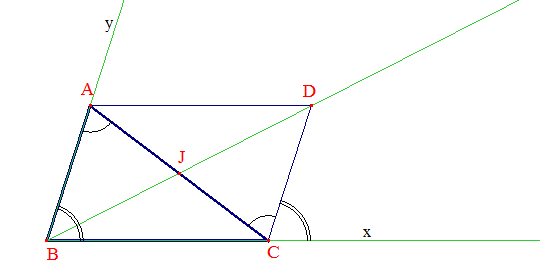
La preuve de ce résultat est très simple en considérant le parallélogramme ADCB obtenu en construisant le point D, symétrique de B par rapport au milieu J de [AC].
♦ i2/ (Euclide, Livre I, XVIII) : si deux côtés d'un triangle n'ont pas même mesure, il en est de même des angles opposés et au plus grand côté est opposé le plus grand angle :
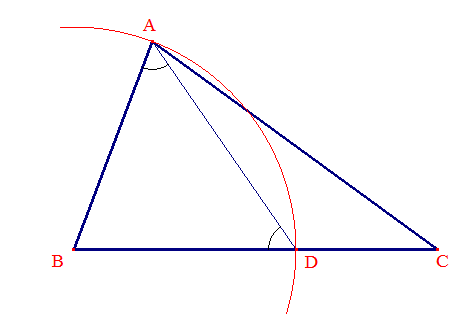
En effet, supposons (ci-dessus) BC > BA. On peut
placer D sur [BC] tel que BA = BD.
On a ^BAD = ^BDA et, d'après i1/, ^BDA > ^BCA,
donc ^BAD > ^BCA. Mais ^BAC > ^BAD puisque ce dernier angle est intérieur à
^BAC. Donc ^BAC > ^BCA.
On montrerait de même ^BAC > ^ABC si BC > AC.
♦
i3/ (Euclide, Livre I, XIX) : si deux angles d'un triangle
n'ont pas même mesure, il en est de même des côtés opposés et au plus grand
angle est opposé le plus grand côté (réciproque de i2).
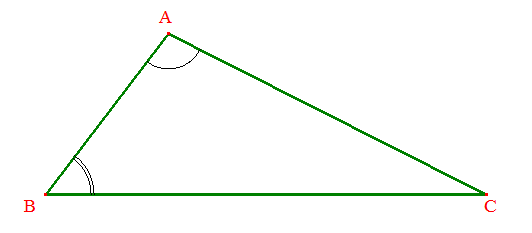
Supposons ^BAC > ^ABC et comparons BC et AC. On ne peut avoir BC = AC sinon le triangle est isocèle en C et on devrait avoir ^BAC = ^ABC. On ne peut avoir BC < AC car selon i2/ nous aurions ^BAC < ^ABC. On a donc BC > AC.
➔ i2/ et i3/ montrent que les angles d'un triangle sont dans le même ordre (au sens des mesures) que les côtés opposés.
♦ i4/ Inégalité triangulaire (Euclide, Livre I, XX) : La mesure de tout côté d'un triangle est inférieur à la somme des mesures des deux autres côtés.
Ce résultat est évident si l'on admet comme postulat que le plus court chemin d'un point à un autre est la « ligne droite » ou que « traverser tout droit » est toujours plus court que « traverser en oblique »... :
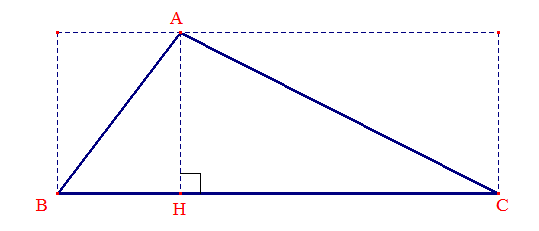
La preuve d'Euclide : sur la figure ci-dessous, prolongeons [BC] et plaçons D tel que CA = CD. [AC] étant intérieur à ^BAD, cet angle est supérieur à ^CAD. Le triangle ACD étant isocèle, on en déduit ^CDA < ^BAD. Selon i3/ on peut conclure que dans le triangle BAD, on a AB < BD. Mais BD = BC + CD, soit : AB < BC + CA.
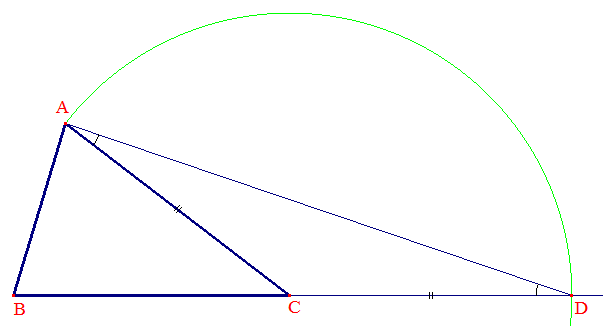
♦ i5/ La mesure de tout côté d'un triangle est supérieure à la différence absolue des mesures des deux autres côtés :
Selon i4/ on a dans tout triangle ABC : BC < AB + AC , AB < BC + AC et AC < AB + BC. Ce qui fournit par exemple AB > BC - AC (1) et AB > AC - BC. Or BC - AC et AC - BC sont opposés, donc AC > | BC - AC |.
∗∗∗
Utiliser les résultats précédents afin de prouver la proposition XXI (Livre I)
:
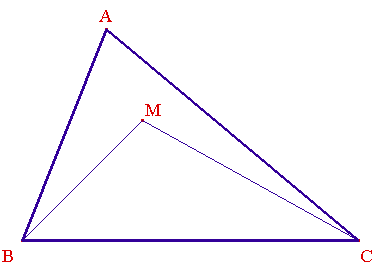
Un triangle ABC étant donné, on construit
intérieurement un triangle BMC
alors BM + MC < BA + AC mais ^BMC > ^BAC
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
BM peut être supérieur à BA : déplacer M vers A' et A' vers C
Si vous séchez après avoir bien cherché : »
|
Réponse : |
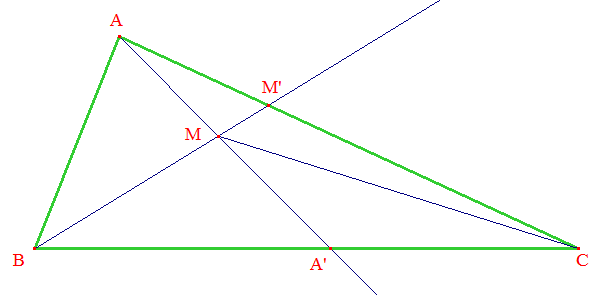
Preuve donnée par Euclide (Livre I, proposition XXI) :
a) M étant intérieur à l'angle ^BAC, la demi-droite [AM) coupe [BC] en un point A'. Selon le résultat i1/, l'angle ^BMA' extérieur au triangle BAA' est supérieur à ^BAM. De même ^A'MC est supérieur à ^A'AC. D'où ^BMC > ^BAC.
b) Étudions maintenant la longueur BM. Le point M étant intérieur à ABC, la demi-droite [BM) coupe [AC] en un point M'. Dans le triangle BAM', on a AB + AM' > BM' (inégalité triangulaire : i4). Ajoutons membre à membre M'C; on obtient :
BA + AC > BM' + M'C.
Dans CM'M, on a CM' + M'M > CM (inégalité triangulaire : i4). Ajoutons membre à membre MB :
CM' + M'B > CM + MB
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez déformer le triangle ABC
et déplacer M
Des deux relations trouvées, on conclut : BA + AC > CM + MB (ou BM + MC), ce qu'il fallait démontrer.