
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
» Résultats sur les séries | Cas des séries entières | Fonctions abéliennes | Équation intégrale d'Abel | Prix Abel |
 Niels Abel
fit ses études au collège de la cathédrale d'Oslo (Christiania
à l'époque) jusqu'en 1821. Dès l'âge de 16 ans,
il découvre les œuvres de Euler et de
Lagrange et cherche à résoudre
l'équation du 5ème degré; mais ses maîtres ne prêtèrent pas attention à ses
recherches. Il s'attaqua alors aux
intégrales
elliptiques tout en continuant à
travailler sur les équations algébriques. Il entre ensuite à l'université d'Oslo
où il présentera (1824) ses premiers résultats sur l'équation du 5ème degré
confirmés par Ruffini qui travaillait indépendamment sur le sujet.
Niels Abel
fit ses études au collège de la cathédrale d'Oslo (Christiania
à l'époque) jusqu'en 1821. Dès l'âge de 16 ans,
il découvre les œuvres de Euler et de
Lagrange et cherche à résoudre
l'équation du 5ème degré; mais ses maîtres ne prêtèrent pas attention à ses
recherches. Il s'attaqua alors aux
intégrales
elliptiques tout en continuant à
travailler sur les équations algébriques. Il entre ensuite à l'université d'Oslo
où il présentera (1824) ses premiers résultats sur l'équation du 5ème degré
confirmés par Ruffini qui travaillait indépendamment sur le sujet.
Grace à une bourse d'études, il se rend à Berlin (1825); il y rencontre Crelle et malgré ses publications dans le journal de ce dernier, les travaux de ce jeune et génial mathématicien laissent indifférente la communauté mathématique. Abel ne renonce pas et se rend à Paris l'année suivante. Mais son mémoire, intitulé Sur quelques propriétés générales d'une certaine sorte de fonctions transcendantes, présenté par Hachette (1826) à l'Académie des Sciences de Paris, fut mésestimé par Gauss et Legendre puis égaré et retrouvé par Cauchy mais, hélas, après la mort d'Abel : victime de la tuberculose à peine âgé de 27 ans, ces travaux ne furent reconnus qu'après sa mort.
Dans ce mémoire était exposé pour la première fois le concept totalement innovant de fonction elliptique basé sur le principe d'inversion des intégrales dites "elliptiques". une nouvelle classe de fonctions transcendantes était ainsi découvertes. Liouville et Jacobi complèteront ses travaux. Ce sera d'ailleurs Jacobi qui comprendra tout le génie du jeune mathématicien en développant la notion de fonction θ (thêta). C'est avec ce dernier qu'Abel recevra, à titre posthume, le grand prix de mathématiques de l'Institut de France (1830). En 1839, son ancien professeur au collège de la cathédrale d'Oslo, Bernt M. Holmboe (1795-1850) publiera ses œuvres complètes.
|
Les équations algébriques et les nombres algébriques : |
Par équation algébrique, on entend une équation du type P(x) = 0 où P est un polynôme pour lequel on précise la nature de la variable et des coefficients : appartenance à tel ou tel anneau ou corps de nombres, comme Z, Q, R ou C.
Si, à 16 ans, Abel pense avoir prouvé la possibilité de résoudre par radicaux l'équation du 5ème degré, c'est à 19 ans qu'il reviendra sur son résultat en prouvant le contraire !
Il est impossible, dans le cas général, de résoudre par radicaux une équation algébrique de degré 5
C'est dire, qu'en dehors de certains cas particuliers, il n'existe pas d'algorithme général applicable à de telles équations.
x6 - x3 - 2 = 0 est résoluble par radicaux dans R : on se ramène au second degré en posant X = x3; on obtient X = - 1 ou X = 2. Les solutions sont alors x = -1 et x = - 3√2 (le symbole 3√ pour signifier racine cubique).
Abel caractérisa une catégorie d'équations algébriques susceptibles d'être résolubles par radicaux, dites aujourd'hui équations abéliennes, dont un représentant élémentaire est xn - 1 = 0 lorsque n est premier, équation que résolut Vandermonde en la ramenant au 5è degré sur une idée d'Abraham de Moivre.
Ces résultats, que Gauss, incrédule, refusa de lire, ne furent publiés qu'en 1826 dans le journal de Crelle. On cherchait à les établir depuis Bombelli avec les travaux de Lagrange, Gauss, Cauchy et Ruffini, utilisant certaines propriétés invariantes des fonctions symétriques des racines. Le français Evariste Galois, contemporain d'Abel, développant la théorie des groupes de substitution, généralisera ces travaux à tout entier premier n > 4.
Courbes et équations algébriques : » Notion de fonction algébrique : »
Nombres algébriques, entiers algébriques :
On doit à Abel (1825) la notion de nombre algébrique de degré n : solution (réelle ou complexe) d'une équation polynomiale P(x) = 0 de degré n à coefficients rationnels (ou entiers, cela revient au même). On parlera d'entiers algébriques lorsque le coefficient de plus haut degré de P est 1 (polynôme unitaire), les autres coefficients étant entiers. Ces nombres seront le socle de fructueuses recherches de la preuve du grand théorème de Fermat.
Corps de nombres algébriques, extension algébrique d'un corps : » » Gauss , Pisot
L'exemple 4 ci-dessus se généralise :
cos(π/n) et de sin(π/n) sont des nombres algébriques de degré n pour tout entier naturel non nul n
» Kummer
Il fut prouvé respectivement en 1873 par Hermite et en 1882 par Lindemann que les nombres e (base des logarithmes népériens) et π ne sont pas algébriques. De tels nombres sont dits transcendants. Cette appellation est due à Liouville (1844), lequel mit "à jour" une première catégorie de tels nombres. On sait depuis Cantor qu'il en existe une infinité non dénombrable :
Nombres de Liouville, fonctions transcendantes : » Non dénombrabilité des nombres transcendants : »
| Notion de groupe, groupe abélien, extension abélienne d'un corps : |
Un groupe G est un ensemble muni d'une loi de composition interne associative admettant un élément neutre et dans lequel tout élément possède un symétrique. Un groupe est dit abélien ou commutatif si sa loi de composition est commutative.
Lois de composition : »
On parle d'extension abélienne pour désigner une extension de corps dont le groupe de Galois est abélien.
» Artin Structures algébriques,
groupes, anneaux, corps, ... : »
| Travaux sur les séries réelles ou complexes : lemme d'Abel | notions sur suites et séries | séries entières |
Introduits afin d'établir des résultats relatifs à la convergence des séries numériques et des séries de fonctions, les théorèmes, règles et lemmes d'Abel son nombreux.
Contre-exemple d'Abel :
Dans ce contexte, Abel mit en défaut (1826) un théorème de Cauchy, énoncé par ce dernier dans son Cours d'analyse, (1821) selon lequel
Si les fn sont continues au point xo et si la série Σfn(x) est convergente dans un voisinage V de xo, alors la fonction limite f ainsi définie dans V est continue en xo.
Abel exhiba la série numérique de terme général fn définie par :
![]()
Cette série converge pour tout x réel. Soit x → f(x) la limite des fn manifestement continues en x = 0 et f(0) = 0 Malheureusement f n'est pas continue en 0 : on montre facilement, par développement en série de Fourrier que ses limites à droite et à gauche en 0 sont respectivement ± π/4.
! Cauchy ne tint pas compte de la remarque du jeune prodige car il reprit le même théorème dans son cours de 1833 !
Étude du contre-exemple d'Abel : » Suites & séries (généralités, convergence) : »
Transformation d'Abel :
Soit une série numérique se présentant sous la forme Σan. On note Rn(m) la somme des termes des rangs n à m, m > n :
Rn(m) = an + an+1 + an+2 + ... am
On a :
Ce qui conduit à :
Rn(m) = bnRn(n) + bn+1[Rn(n+1) - Rn(n)] + bn+2[Rn(n+2) - Rn(n+1)] + ... + bm[Rn(m) -Rn(m-1)]
Et on voit que Rn(m) peut être réécrit sous la forme dite transformation d'Abel :
Rn(n) (bn - bn+1) + Rn(n+1)(bn+1 - bn+2) + ... Rn(m-1)(bm-1 - bm) + bmRn(m)
En application de cette transformation, on établit :
Théorème 1 :
Soit une série réelle ou complexe de la forme Σanbn . Supposons alors que :
les Rn(k) admettent un majorant M à partir d'un certain rang N ≥ n.
Dans ces conditions, la série Σanbn est alors convergente (puisque son reste tend vers 0). Un cas particulier très pratique est le suivant :
Théorème 2 :
Soit Σanbn une série numérique où (an) désigne une suite numérique positive décroissante et Σbn une série (réelle ou complexe) dont les sommes partielles sont bornées : il existe k > 0, | b0 + b1 + ... + bn | < k pour tout n. Alors les sommes partielles de Σanbn sont aussi bornées et on a :
| aobo + a1b1 + ... . anbn | < kao
On a en corollaire de ce théorème :
Critère (ou règle, ou test) d'Abel pour les séries :
Si les sommes partielles de la série de terme général an (réel ou complexe) sont bornées et si (bn) est une suite réelle positive décroissant vers 0, alors la série Σanbn est convergente.
Critère de Dedekind :
» Critère
de Dirichlet :
»
| Résultats sur les séries entières, lemme d'Abel : » notions sur suites et séries |
Une série entière (ou série de puissances) est une série Σun = uo + u1 + u2 + ... + un + ... dont le terme général un est de la forme anzn où an est un réel fonction de n et z un nombre réel ou complexe. Il s'agit d'un cas particulier de série de fonctions dont le terme général est de la forme fn(z) où fn est une fonction numérique. Dans les deux cas, la convergence (finitude de la somme) dépend de la valeur de la variable z.
Lemme d'Abel pour les séries entières et rayon de convergence :
Soit Σanzn une série entière réelle ou complexe. Si, pour un complexe zo, la suite de terme général anzon est bornée, alors la série Σanzn est absolument convergente (la série des modules converge) pour tout z tel que |z| < |zo|.
Preuve : par hypothèse, il existe un réel positif M tel que anzon < M. On a alors |anzn| = |anzon| × |z/zo|n < M|z/zo|n. Or |z/zo|n est le terme général d'une série géométrique convergente puisque |z/zo| < 1. La série entière est donc absolument convergente et donc, a fortiori, convergente.
➔ On remarquera que la suite de terme général anzon est bornée si, en particulier, la série Σanzon est convergente.
Rayon de convergence d'une série entière :
En conséquence du lemme d'Abel ci-dessus, si une série entière converge pour une valeur zo, elle convergera pour tout z tel que |z| < |zo|. Si une série entière diverge pour une valeur zo, elle divergera pour tout z tel que |z| > |zo|. On en déduit l'existence d'un réel positif tel que la série converge pour tout |z| < R et diverge pour tout |z| > R. Le cas |z| = R restant litigieux :
Le rayon de convergence de la série Σanzn est la borne supérieure R (finie ou non) de l'ensemble des réels positifs tels que la suite des anzn soit bornée. Le disque ouvert de centre 0, de rayon R (resp. intervalle ]-R,+R[ dans le cas réel) est le disque (resp. intervalle) de convergence.
! On ne confondra pas les concepts de série absolument convergente et de série normalement convergente : pour laquelle il existe une série Σun convergente à termes positifs pour laquelle on a pour tous n et z : | Σanzn | ≤ un.
Calcul du rayon R de convergence :
Pour une série Σanzn, réelle ou complexe, la règle de d'Alembert et le critère de Cauchy pour les séries (» 5b) permettent d'écrire :
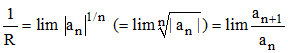
➔ Lorsque la limite trouvée est nulle, le rayon de convergence est infini. C'est ainsi, par exemple que la série Σxn/n! converge pour tout x de R. Cette convergence est uniforme (» théorème 3 ci-dessous) vers ex.
Séries de fonctions (cas général) : »
Théorème 3 (pour les séries entières) :
Soit Σanzn une série entière définie dans R ou C :
➔ Rappelons que la convergence normale entraîne la convergence uniforme d'une telle série à valeurs dans un espace métrique complet : cas particulier d'une série de fonctions.
Théorème 4 (pour les séries entières) :
Dans le disque de convergence (intervalle dans le cas réel), la continuité de la somme d'une série entière est assurée :
Soit Σanzn une série entière dans R ou C de rayon de convergence R non nul, de somme f, fonction de z. alors :
f est continue pour tout | z | < R.
Si la série ΣanRn est convergente, alors f admet ΣanRn comme limite au point R, ce qui assure la continuité de f au point R.
Un énoncé réciproque (théorème de Tauber) : »
Théorème 5 (pour les séries entières) :
Dans le cas général d'une série de fonctions convergente Σanfn(z) = f(z), la possibilité de dériver ou d'intégrer terme à terme la série afin d'obtenir comme somme la dérivée de f ou une primitive n'est assurée que sous certaines conditions de convergence uniforme. Le cas des séries entières est moins restrictif :
i/ En dérivant ou intégrant terme à terme une série entière, on obtient une série entière de même rayon de convergence.
ii/ Dans le cas réel ou complexe, la série Σanzn de rayon de convergence R, de somme f(z) a pour dérivée la série Σnanzn-1 de somme f '(z) sur le disque ouvert de convergence | z | < R.
iii/ Dans le cas réel, avec les notations de iii/, la série Σanxn+1 /(n + 1) converge dans | x | < R et sa somme est la primitive nulle en zéro de la fonction f : intégrale de f sur [0,x], | x | ≤ ρ < R.
|
Règle d'Abel pour la convergence d'une intégrale généralisée : |
On suppose que f est une fonction positive, continue et décroissante vers 0 sur [a, +∞[ et que l'intégrale de g sur tout intervalle [a,λ], avec λ > a , existe et est bornée. Dans ces conditions, l'intégrale :
![]()
est convergente, ceci pour exprimer que la limite, lorsque λ tend vers +∞, de l'intégrale sur [a,λ] du produit fg existe et est finie).
| Équations intégrales d'Abel et inversion (1823) : |
L'équation intégrale d'Abel est née d'un problème de mécanique résolu et publié en 1823, avec d'autres sujets, par le jeune mathématicien sous le titre Solution de quelques problèmes à l'aide d'intégrales définies. Volterra reprend ici le sujet (» réf. 6) :
L'équation intégrale d'Abel (1) ci-dessus, peut s'écrire :

Abel résolut plus généralement ( 0 < α < 1) :

dont la solution peut prendre la forme :

Cette équation intégrale (linéaire de 1ère espèce) est liée à l'intégrale de Riemann-Liouville.
Une autre équation intégrale d'Abel (de seconde espèce) est :
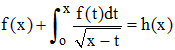
C'est un cas particulier d'équation intégrale de Volterra.
Volterra et la notion d'équation intégrale : » Équation intégrale de Fredholm : »
| Les intégrales et fonctions elliptiques, fonctions abéliennes : |
Considérée comme l'œuvre maîtresse d'Abel (Mémoire sur une propriété générale d'une classe très étendue de fonctions transcendantes, 1826), l'étude de ces fonctions, dite elliptiques depuis Legendre, provient des premières tentatives de rectification de l'ellipse conduisant aux intégrales elliptiques, préalablement étudiées par Lagrange et Legendre, et dont le calcul par quadrature, donc la recherche d'une primitive de l'intégrande (fonction à intégrer), est impossible à l'aide de fonctions "usuelles".
! Avant de le publier, Abel confia son manuscrit à Cauchy qui l'égara ! Ce ne fut qu'en 1841, 12 après la mort d'Abel, qu'il fut retrouvé et publié par l'Académie des sciences.
Ces intégrales sont des fonctions de leur borne supérieure. Par analogie avec le cercle (fonctions circulaires), l'idée générale (et géniale) d'Abel, et de Jacobi la même année, fut de renverser le problème en étudiant leurs "réciproques".
On parle alors de fonctions elliptiques mettant ainsi en évidence une nouvelle classe de fonctions transcendantes. En se plaçant dans le plan complexe, Abel découvre une propriété étonnante de ces fonctions : leur double périodicité. Il est alors permis d'étudier ces fonctions de façon formelle, indépendamment de leur genèse en tant que fonction méromorphe doublement périodique.
Les travaux d'Abel furent poursuivis par Gauss et Jacobi et par de très nombreux mathématiciens du 19è siècle dont Gudermann, Riemann, Clebsch et, en France, Liouville, Bouquet et Briot, Poincaré.
En savoir un peu plus sur les intégrales elliptiques : »
Abel généralisa l'étude des intégrales elliptiques à une classe d'intégrales dites aujourd'hui abéliennes dont la forme générale peut s'écrire :
![]()
où F est une fonction rationnelle de x et y (polynôme ou quotient de deux polynômes en x et y), y étant lié à x par une équation algébrique φ(x,y) = 0.
Lorsque φ(x,y) est de la forme y2 - P(x) = 0, y est un radical de la forme ±√P(x) et si P est un polynôme de d°3 ou 4 (resp. de d° > 4), on retrouve les intégrales elliptiques (resp. hyperelliptiques).
|
Variétés abéliennes : |
Il s'agit de variétés algébriques particulières dont la définition et l'étude nécessitent des requis dépassant les objectifs de cette chronologie. Le lecteur désireux d'en savoir plus pourra, par exemple, consulter :
Le prix Abel :
Afin de pallier l'absence d'un prix Nobel de mathématiques, le gouvernement norvégien a créé en 2002, un « prix Abel »
(» réf.12) à l'occasion du bicentenaire de sa naissance (5 août 1802). D'un montant annuel de 6 000 000 de couronnes, soit 600 000 €, réévalué à 7 500 000 couronnes en 2020, environ 650 000 euros, il concurrence, par sa notoriété, la très prestigieuse et convoitée médaille Fields cependant très peu dotée (environ 10 000 €), accordée tous les quatre ans et ne pouvant être attribuée à des mathématiciens de plus de 40 ans. Le premier prix Abel a été décerné le 3 avril 2003 au mathématicien français Jean-Pierre Serre :| 2003 | Jean-Pierre Serre (Collège de France) |
Pour son rôle central dans l'élaboration de la forme moderne de nombreux domaines des mathématiques. Le chercheur est particulièrement récompensé pour ses travaux dans le domaine de la topologie, la géométrie algébrique et la théorie des nombres. |
| 2004 | Michael Atiyah
(univ. Edimbourg)
et Isadore Singer (MIT). |
Pour leur découverte et la preuve du théorème d'index, réunissant topologie, géométrie et analyse, et leur rôle exceptionnel dans la construction de nouveaux ponts entre les mathématiques et la physique théorique. |
| 2005 | Peter D. Lax (univ. New York). | Pour ses contributions révolutionnaires à la théorie et à l'application des équations aux dérivées partielles et au calcul de leurs solutions. |
| 2006 | Lennart Carleson, suédois (Institut Royal de Technologie, Stockholm). | Pour ses contributions profondes et fondamentales à l'analyse harmonique et à la théorie des systèmes dynamiques lisses. |
| 2007 | Srinivasa Varadhan, indo américain (univ. New York). | Pour ses contributions fondamentales à la théorie des probabilités et en particulier pour la création d'une théorie unifiée des grands écarts (» réf.13). |
| 2008 |
Jacques Tits
(Collège de France) et
John G. Thompson (univ. Floride). |
Pour leurs réalisations profondes en algèbre et en particulier pour façonner la théorie moderne des groupes. |
| 2009 | Mikhaïl Gromov (IHES, France). | Pour ses contributions révolutionnaires en géométrie. |
| 2010 | John Tate (univ. Austin, USA). | Pour son impact vaste et durable en théorie des nombres. |
| 2011 | John Milnor (univ. S. Brook, New York). | Pour ses découvertes pionnières en topologie, géométrie et algèbre. John Milnor est récipiendaire de la médaille Fields 1962. |
| 2012 | Endre Szemerédi, hongrois (univ. du New Jersey, USA) | Pour ses contributions fondamentales aux mathématiques discrètes et à l'informatique théorique et en reconnaissance de l'impact profond et durable de ces contributions sur la théorie additive des nombres et la théorie ergodique. |
| 2013 | Pierre Deligne, belge (IAS, Princeton). | Pour ses contributions fondamentales à la géométrie algébrique et leur impact sur la théorie des nombres, la théorie des représentations et les domaines connexes. |
| 2014 | Yakov Sinaï, russo américain (univ. Princeton/Institut Landau, Moscou). | Pour ses contributions fondamentales aux systèmes dynamiques, à la théorie ergodique et à la physique mathématique. |
| 2015 | John Nash (MIT) et Louis Nirenberg (uni. New York). | Pour des contributions marquantes et fondamentales à la théorie des équations aux dérivées partielles non linéaires et ses applications à l'analyse géométrique. |
| 2016 | Andrew Wiles (Grande Bretagne). | Pour sa démonstration étonnante du dernier théorème de Fermat au moyen de la conjecture de modularité portant sur les courbes elliptiques, ouvrant une nouvelle ère dans la théorie des nombres. |
| 2017 | Yves Meyer, français (ENS Cachan). | Pour son rôle central dans le développement de la théorie mathématique des ondelettes. |
| 2018 | Robert Langlands (IAS Princeton). | Pour son "programme" visionnaire reliant la théorie de la représentation (des groupes de Lie) à la théorie des nombres. |
| 2019 | Karen Uhlenbeck professeur émérite de l’université du Texas (Austin, États-Unis), actuellement maître de recherches à Princeton. Première femme récipiendaire de ce prix depuis sa création. | Pour ses travaux innovants dans l'étude des solutions de systèmes d'équations aux dérivées partielles sur des variétés différentiables (en lien avec la théorie de jauge) et pour l'impact fondamental de son travail sur l'analyse, la géométrie et la physique mathématique. |
| 2020 | Gregory Margulis (Yale university) et Hillel Furstenberg, israélo-américain (univ. Jerusalem). | Pour leurs travaux fondateurs dans l'utilisation de méthodes probabilistes et des systèmes dynamiques en théorie des groupes, théorie des nombres et combinatoire. G. Margulis est récipiendaire de la médaille Fields 1992. |
| 2021 |
Laszlo Lovasz,
hongrois
(univ. Budapest) et Avi Wigderson, israélien (IAS Princeton). |
Pour leurs contributions fondamentales à l'informatique théorique et aux mathématiques discrètes (théorie de la complexité, » Stephen Cook, cryptographie). |
| 2022 | Dennis Parnell Sullivan, Stony Brook university, États-Unis. | Pour ses contributions révolutionnaires à la topologie dans son sens le plus large, en particulier ses aspects algébriques, géométriques et dynamiques. |
| 2023 | Luis A. Caffarelli, univ. Austin, États-Unis. | Pour ses contributions fondamentales à la théorie de la régularité pour les équations aux dérivées partielles non linéaires, y compris les problèmes de frontière libre et l'équation de Monge-Ampère. |
| 2024 | Michel Talagrand (1952-), univ. Paris-Jussieu et CNRS, France. | Pour ses contributions révolutionnaires à la théorie des probabilités et à l'analyse fonctionnelle, avec des applications remarquables en physique mathématique et en statistique. Homepage |
➔ Pour en savoir plus :