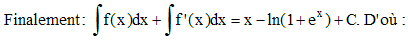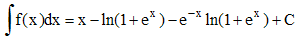ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» voir aussi : Exemples d'intégration par parties | primitives de 1/sin x et 1/cos x | primitives de e1/x |

1 - 
2 -
 (procéder par décomposition en éléments simples)
☼
(procéder par décomposition en éléments simples)
☼
3 - 

4 -
![]()
Indications : x/a est compris entre 0 et 1 : on posera x = a.sin
t avec t croissant de 0 à π/2; cos
t est alors positif.
5a -

Indications : on posera
√(t2 -
1) = u. Élever au carré et différentier...
5b -

6 -

Indications
: Dans un premier temps, poser t =
tan(x/2) afin de se ramener à l'intégrale d'une fraction rationnelle. Poser
ensuite u = t/√3.
On remarquera
utilement que 3u2
+ 1 peut s'écrire u2 + 1 + 2u2 et on pourra calculer la
dérivée de u/(u2 + 1).
7
-
![]()
8 -
![]() :
☼
:
☼
9
-
![]()
10
-
![]()
11
- 
12
-

13
- ![]()
14 -

15 - On pose f(x) = e-xln(1 + ex). Calculer f(x) + f '(x). En déduire les primitives de f.
16 - 
17 -
![]() ☼
☼
18 -
![]() :
☼
:
☼
19
-
 : ☼
: ☼
Si vous séchez après avoir bien cherché : ››››
|
Réponses : |
1 - La division de x4 + 1 par -x3 + x fournit d'abord -x + (x2 + 1)/(x - x3). Or x - x3 = x(1 - x)(1 + x). On en déduit :
![]()
On obtient facilement par identification à l'écriture initiale de f(x) : a = 1, b = 1 et c = -1. Finalement :

2 - La décomposition en éléments simples fournit ici 1 - 2/(1+ t) + 2/(1+ t)2. D'où, très simplement :

3 - On obtient sans difficulté :



Une primitive de f sera donc :

Et l'intégrale sur l'intervalle [0,1] sera 2 - ln(3) - π√3/9 car ln(1) = 0, Atn√3 = π/3 et Atn(1/√3) = π/6.
4 - En posant x = a.sin t, on a dx = a.cos t.dt et l'intégrale devient :

➔ Si l'on avait voulu calculer les primitives de l'intégrande, on aurait remarqué que t = Asn(x/a), sin 2t = 2sin t.cos t et cos2 t = 1 - x2/a2. D'où :

5a - Soit J l'intégrale cherchée. En posant √(t2 - 1) = t - u et en élevant au carré, on obtient 1 - 2ut + u2 = 0. On différentie : (u - t).du = u.dt, ce qui fournit dt en fonction de u que l'on remplace dans l'intégrale en notant que les bornes en u = t - √(t2 - 1) deviennent 1 en t = 1 et x - √(x2 - 1) en t = x :

En remarquant que x - √(x2 - 1) n'est autre que x + √(x2 - 1), il s'avère finalement que :

➔ Cette intégrale n'est autre que Argcoshx. On se reportera aussi à la page de Vincenzo Riccati.
5b - Notons I l'intégrale cherchée. En posant u = √(t2 - 1) et v' = 1, on obtient :
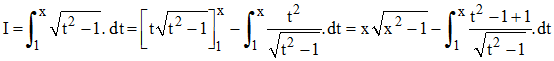
Par conséquent :

Finalement :

6 - Cherchons tout d'abord une primitive, encore notée I, de l'intégrande. Avec t = tan(x/2), on a dt = ½(1 + t2)dx et cos x = (1 - t2)/(1 + t2). En remplaçant, on obtient après simplification :
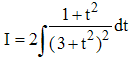
Le changement de variable t = u√3 conduit alors à :

Les indications données fournissent finalement :

Cette primitive doit être calculée pour x variant de 0 à π/2 : t varie donc entre 0 et 1 u varie entre 0 et 1/√3

» lorsque l'intervalle d'intégration devient [0,π], on a un problème dû à u= t√3 = √3tan(x/2) : la tangente devient infinie positive et l'intégrale devient généralisée. Or lorsque u tend vers +∞, Atan tend vers π/2. Par conséquent :
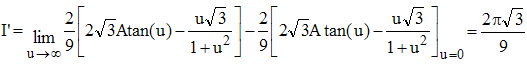
7 - Calculons tout d'abord une primitive de la fonction sin(ln x); à une constante additive près, nous avons :
∫sin(ln x)dx = x.sin(ln x) - ∫x.cos(ln x)dx + k = x.sin(ln x) - [ x.cos(ln x) + ∫sin(ln x)dx ].
D'où ∫sin(ln x)dx = ½ (x.sin(ln x) - x.cos(ln x))
On en déduit F(t) = [½
x(sin(ln x) - cos(ln x))]![]() = ½ t(sin(ln t) - cos(ln t))
+ 1
= ½ t(sin(ln t) - cos(ln t))
+ 1
9 - Appelons J cette intégrale. On intègre par parties sachant que la dérivée de Atanx est 1/(1 + x2) :
 »
Arc tangente :
»
Arc tangente :
Mais, par division, on a x3/(1 + x2) = x - x/(1 + x2) et cette dernière fraction rationnelle s'intègre immédiatement :

10 - On a t2 = x + 1 et dx = 2t.dt. D'où :
![]()
11 - On a t ≥ 0 et t2 = ex - 1 ≥ 0 et 2t.dt = ex.dx. D'où :

Par conséquent :

12 - On a dx = 2(1 + tan2z)dz. On remplace et, en remarquant que 1 + tan2z = 1/cos2z, on obtient :

13 - En ajoutant la partie imaginaire proposée, il s'agit d'intégrer ex(i-1). On trouvera sans difficultés :
![]()
dont la partie réelle est l'intégrale I cherchée, soit : ½(1 - 1/e2π).
14 - Le changement de variable indiqué ramène facilement à l'intégration d'une fraction rationnelle :
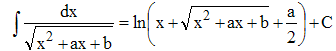
➔ Si le radicande est ax2 + bx + c avec a > 0, la division par a ramène au résultat plus général :

» Le cas a < 0 conduit immédiatement à un arc sinus.
15 - On vérifie sans difficultés que f(x) + f '(x) = 1/(1 + ex). On peut écrire :