
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» Première notion de variable aléatoire | Cas d'un couple| Cas discret | Cas d'un couple statistique |
Avec l'apparition de la théorie de la mesure (initiée par Borel), une théorie moderne, voire abstraite, des probabilités s'est développée dans la première moitié du 20è siècle. Une probabilité sur un ensemble (espace probabilisé) apparaît alors comme une mesure définie dans cet ensemble, et à des fins pratiques portant sur l'usage de l'intégration au sens de cette mesure (fonctions de répartition, densité de probabilité), il est alors fait usage de variables aléatoires absolument continues pour signifier que leurs fonctions de répartition est absolument continue. L'exposé ci-dessous se restreint au cadre "élémentaire" de l'intégrale de Cauchy équivalente à celle de Riemann pour les fonctions continues. Pour un aspect plus théorique, on pourra consulter les liens indiqués in fine (réf. 6 à 10).
Lorsqu'une variable aléatoire X peut prendre toute valeur réelle, on parle de variable continue. Dans ce cas, il ne s'agira plus de calculer une probabilité d'apparition d'une valeur donnée mais d'un intervalle de valeurs. Daniel Bernoulli fut un pionnier en la matière. Afin d'illustrer cette notion, étudions un exemple simple :
|
Loi uniforme, également dite loi rectangulaire, sur un intervalle de R : |
On considère un intervalle [a,b] de R dans lequel on choisit un point d'abscisse x au hasard, sans autre condition que a ≤ x ≤ b. Il s'agit de la loi uniforme sur [a,b] :
Si x' et x" sont deux valeurs choisies dans [a,b], dire que la distribution de probabilités est uniforme signifie que la probabilité de réalisation de l'événement {x' ≤ x ≤ x"} est proportionnelle à x" - x'.
Plus précisément :
il existe un réel k ne dépendant pas de x' et x" tel que Prob{x' ≤ X ≤ x"} = k(x" - x')
Si x' = a et x" = b, on a 1 = k(b - a), ce qui fournit k = 1/(b - a).
La notion de densité de probabilité :
Soit maintenant deux valeurs de X infiniment proches x et x + dx. La probabilité Prob{x ≤ X ≤ x + dx} = kdx = dx/(b - a) est infinitésimale. Notons dF(x) cette probabilité. On a donc dF(x) = dx/(b - a), ce que l'on note plus simplement dF/dx = 1/(b - a).
Posons :
f(x) = dF/dx
La fonction f est la densité de probabilité de X au point x. Elle apparaît comme fonction fonction dérivée d'une fonction F appelée fonction de répartition de la variable aléatoire continue X :

La densité de la loi uniforme sur [a,b], définie ci-dessus au moyen de k, est alors :

C'est la fonction caractéristique de l'intervalle [a,b], souvent notée 1[a,b].
➔ On définirait de même la loi uniforme sur une aire ou dans un volume homogène. Le paragraphe suivant justifiera l'appellation loi rectangulaire pour la loi uniforme sur un intervalle.
En conclusion de cette introduction :
Face à un phénomène aléatoire continu, il s'agit de calculer la probabilité Prob(x < X < x + dx). Ce calcul conduit à une expression de la forme f(x)dx où la fonction x → f(x) est la densité de probabilité du phénomène. Ce qui est nécessaire et suffisant pour décrire le phénomène étudié. On trouvera ci-dessous deux liens conduisant à une telle recherche :
La Loi uniforme sur le cercle : » La loi exponentielle : »
D'autres lois continues, plus complexes, mises en place par les mathématiciens, statisticiens physiciens ou astronomes sont étudiées dans Chronomath et précisées in fine.
|
Synthèse : |
X désignant une variable aléatoire numérique continue, la fonction de répartition F de X, exprime la probabilité de l'événement X ≤ x ou bien, indifféremment par continuité, l'événement X < x. C'est une fonction fonction F : R → [0,1] de la forme :
où f, appelée densité de probabilité de X, désigne une fonction numérique positive continue, intégrable sur R et telle que (condition fondamentale) :
Inversement :
Toute fonction positive continue ou continue par morceaux, intégrable sur R, d'intégrale égale à 1, est la densité de probabilité d'une variable aléatoire continue dont la fonction de répartition F est définie par :
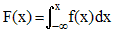
Fonction de répartition et aire sous la courbe représentative de la densité :
La probabilité d'un intervalle borné ou non s'interprète comme une aire. En effet, pour deux valeurs de X infiniment proches x et x + dx, on est en droit d'estimer que sur l'intervalle infiniment petit de longueur dx, la distribution de probabilité est uniforme :
Prob(x < X < x + dx) = kxdx
où kx, fonction du phénomène étudié, dépend de x. En posant kx = f(x), on a : Prob(x < X < x + dx) = f(x)dx. Par sommation, en notant dF(x) = f(x)dx, l'intégrale :
est la fonction de répartition de X et s'interprète comme la probabilité de réalisation de l'événement X ∈]-∞,x[ : Prob(X < x).

Pour une valeur a de X donnée, Prob(X < a) = F(a) s'interprète comme l'aire (en vert) sous la courbe représentative de f, densité de probabilité de X.
Pour deux valeurs a et b de x, a < b, F(b) - F(a) s'interprète comme l'aire (en jaune) :

L'intégrale sur R tout entier de f correspond à Prob(X∈R), c'est dire que :
Remarques :
Dans ce cas "continu", tous les signes < peuvent être remplacés par ≤ . La probabilité de l'événement Prob(X = x) est nulle;
Prob(X < x) = Prob(X ≤ x);
Prob(a ≤ X ≤ b) = Prob(a ≤ X < b) = Prob(a < X ≤ b) = Prob(a < X < b).
| Médiane d'une loi continue : |
Comme dans le cas discret, la médiane d'une variable aléatoire X est la valeur md de X pour laquelle la fonction de répartition est égale à 1/2 :
F(md) = Prob(X ≤ md ) = 1/2
Par exemple : la médiane de la loi uniforme sur [a,b], introduite ci-dessus, est (a +b)/2 : valeur médiane du segment. Ce qui semple très logique...
| Espérance mathématique (ou moyenne) : |
Chaque produit xi × Prob(X = xi) du cas discret devient ici un élément différentiel x × dF(x) = x × f(x)dx. La somme des xi × Prob(X = xi) du cas discret devient la somme au sens de l'intégration. L'espérance mathématique ou moyenne de X est ainsi le nombre :
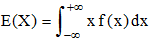
Lorsque la densité est nulle en dehors d'un intervalle J, l'intégrale ci-dessus se réduit à une intégration sur J. Un exemple est donné par la loi exponentielle.
i Lorsqu'on se place dans un espace probabilisé abstrait (Ω,τ,P), l'espérance de X s'écrira :
| Variance, écart-type, loi centrée réduite : |
♦ La variance d'une variable aléatoire continue est, comme dans le cas discret, l'espérance de la moyenne des carrés de ses écarts par rapport à sa moyenne m = E(X) :
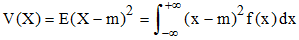
et par linéarité de l'intégrale, on retrouve la formule de König :
V(X) = E(X2) - [E(X)]2
On peut voit là le lien avec la notion, en sciences physiques, de moment d'inertie.
♦ L'écart type σ d'une variable aléatoire est la racine carrée de sa variance : il renseigne sur la dispersion des valeurs de la variable autour de sa moyenne. » Huygens
♦ Centrer une variable aléatoire X, c'est faire le changement de variable X' = X - E(X); on a alors E(X') = 0.
♦ Réduire une variable aléatoire X, c'est faire le changement de variable X'= X/σ; on a alors σ(X') = 1.
➔ Une variable centrée réduite s'obtient donc par la transformation affine X' = (X - m)/σ.
Il est facile de vérifier les propriétés suivantes :
Espérance : E(aX + b) =aE(X) + b.
Variance : V(aX + b) = a2V(X)
en utilisant
la formule de Koenig
En cas d'indépendance
statistique (»
déf.) : V(X + Y) = V(X) + V(Y)
| Moments d'une variable aléatoire continue : |
Cette notion permet de généraliser les définitions précédentes (moyenne et variance) : on appelle moment d'ordre k, l'espérance mathématique de la variable Xk :
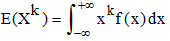
Si k = 1, on retrouve l'espérance mathématique usuelle et si k = 2, la variance.
| Couple de variables aléatoires continues (variable aléatoire à deux dimensions) : |
Considérons un couple (X,Y) de variables aléatoires continues pouvant prendre toute valeur sur R × R. Tout comme dans le cas d'une variable, pour des valeurs de X et Y infiniment proches x et x + dx d'une part et y et y + dy , on est en droit d'estimer que sur le pavé infiniment petit d'aire dxdy, la distribution de probabilité est uniforme :
Prob(x < X < x + dx, y < Y < y + dy) = kx,ydxdy
où le coefficient kx,y, fonction du phénomène étudié, dépend de x et de y. En posant kx,y = f(x,y), on a :
Prob(x < X < x + dx et y < Y < y + dy) = f(x,y)dxdy
On dit que f est la densité de probabilité du couple (X,Y). Par sommation, en notant dF(x,y) = f(x,y)dx, l'intégrale double :
 »
la notion d'intégrale double
»
la notion d'intégrale double
est la fonction de répartition du couple aléatoire (X,Y). Cette fonction s'interprète comme la probabilité de réalisation de l'événement (X,Y)∈]-∞,x[ × ]-∞,y[, conjonction des événements [X < x] et [Y < y] :
F(x,y) = Prob([X < x]∩[Y < y])
Connaissant la fonction de répartition F et lorsque cette dernière est de classe C2 (admettant des dérivées partielles continues d'ordre 1 et 2 par rapport à x et y, selon le théorème de Schwarz :
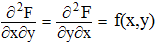
Par définition, la fonction de répartition (ou la densité) f vérifie :

Indépendance d'un couple de variables aléatoires continues :
On dit que X et Y sont indépendantes en probabilité lorsque la densité f du couple (X,Y) est le produit des densités φ et ψ de X et de Y :
∀x,∀x : f(x,y) = φ(x) × ψ(y)
Dans un tel cas :
Quelques lois continues étudiées dans ChronoMath :
La loi uniforme (définie ci-dessus) | La loi exponentielle (dite durée de vie sans vieillissement)
La loi de Laplace-Gauss, dite normale | La loi de Pearson dite du χ2 (khi2) | La loi de Student, dite loi t.
2. Exercice où l'on établit la distribution de Cauchy : loi uniforme sur le cercle
3. La loi de probabilité exponentielle (durée de vie sans vieillissement)
4. Étude d'une loi continue définie par sa fonction de répartition, densité espérance mathématique, variance
5. Montrer que la loi de Cauchy (exercice 1 ci-dessus) n'admet ni valeur moyenne, ni variance.
➔ Pour en savoir plus :
Tout cours 2è année de licence de mathématiques.
Probabilités - Combinatoire -Statistique, par Pierre Louquet et A. Vogt, Éd. Armand Colin, Paris - 1971.
Variables aléatoires discrètes et à densité, par
Jean-Christophe Breton, (univ. Rennes1) :
https://perso.univ-rennes1.fr/jean-christophe.breton/Fichiers/proba_L2.pdf
Lois de probabilité usuelles, par Anthony Phan, univ.
Poitiers :
http://wwwmathlabo.univ-poitiers.fr/~phan/downloads/enseignement/lois-usuelles.pdf
Probabilités, par Bernard Vauquois, Éditions Hermann.
Notions fondamentales de la théorie des probabilités par M. Métivier, Éd. Dunod, Paris - 1968.
Bases mathématiques du calcul des probabilités, par J. Neveu, Éd. Masson, Paris - 1964.
Mathématiques L2 : Cours complet
avec 700 tests et exercices corrigés
ouvrage collectif
sous la direction de Jean-Pierre Marco,
Éd. Pearson Education - Paris, 2007
Théorie des probabilités (pour la préparation à
l'agrégation), par Sébastien Martineau (ENS Lyon) :
http://perso.ens-lyon.fr/sebastien.martineau/Cours_proba.pdf
Rappels de théorie de l'intégration et des probabilités (ENS) : http://www.math.ens.fr/statenaction/PDF/Rappels.pdf