ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 VANDERMONDE Alexandre Théophile,
français, 1735-1796 |
Fils de médecin, Alexandre Théophile commença des études de droit. Mais sa rencontre avec d'Alembert l'entraine vers sciences dont, principalement, les mathématiques (il fut un élève d'Alexis Fontaine) et la chimie. Il entre à l'Académie des sciences à 36 ans en tant qu'adjoint-géomètre suite à son Mémoire sur la résolution des équations (1771).
Vandermonde est, avec l'abbé Henri J.-B.
Grégoire, à
l'origine de la création du CNAM, Conservatoire
des Arts et Métiers, fondé sous la Révolution par la Convention en
1794, la même année que l'École polytechnique et l'École normale supérieure. Un
an avant sa mort, il fut élu membre à part entière de l'Académie des
sciences dès sa restauration en 1795.
Ami de Monge, proche de Lavoisier et de Berthollet, Vandermonde traverse sans encombres, malgré son implication dans différentes commissions auprès du Comité de Salut public, la difficile période de la révolution française de 1789. Il intervint également dans la mise en place du système métrique (1790).
i Henri J.-B. Grégoire (1750-1831), français, évêque de Blois, député à la Convention à qui l'on doit l'abolition de l'esclavage et dont l'influence resta importante sous l'Empire et la Restauration. Ses cendres reposent depuis 1989 au Panthéon près de Monge et de Condorcet, également transférés lors du bicentenaire de la Révolution.
i Claude Berthollet (1748-1822), chimiste français découvreur, entre autres contributions, de l'eau de Javel.
Les équations algébriques :
Apprécié par Kronecker et Lagrange, le Mémoire sur la résolution des équations de 1771 (» réf.1) traite de la résolution des équations algébriques de degré au moins égal à 4 et annonce ce que l'on nommera, avec Jordan et Galois, la théorie des groupes de substitutions.
Dans le même mémoire, Vandermonde traite des polynômes cyclotomiques et cherche à prouver que l'équation xn = 1 d'inconnue complexe, est résoluble par radicaux (expression des racines au moyen de radicaux arithmétiques).
Sur une idée de de Moivre, il mène à bien la résolution de l'équation x11 - 1 = 0 dont Gauss s'inspirera dans son traité Disquisitiones arithmeticae de 1801. On pourra consulter sur ce sujet le lien 3 infine.
Les travaux de Vandermonde portent par ailleurs sur les équations linéaires et les déterminants : Mémoire sur l'élimination (1772), avec le déterminant portant son nom ainsi que sur le sujet des facultés analytiques, définies par :
[a]n = a(a - 1)(a - 2)...(a - n +1)
dont les propriétés s'avèrent semblables à celles des puissances et trouvent leur usage en analyse.
| Déterminant de Vandermonde (et matrices de Vandermonde) : |
C'est le déterminant d'ordre n rencontré, par exemple, dans les problèmes d'interpolation polynomiale. Les ai désignant des scalaires réels ou complexes (1 ≤ i ≤ n), son expression et sa valeur sont :
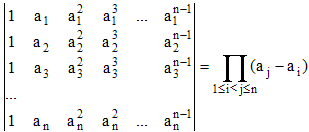
La matrice correspondante est appelée matrice de Vandermonde.
Exemple : dans le cas n = 3, considérons le déterminant :
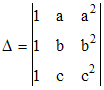
Si a = b ou a = c ou b = c, Δ est nul. Calculons ce déterminant suivant la colonne 1 :
soit :
Considérons ce développement comme un polynôme de variable a. Il s'annule si a = b et si a = c. on peut donc mettre (a - b) et (a - c) en facteur, ou encore (c - a) et (b - a). Considéré en tant que polynôme de la variable b, il s'annule pour b = c : on peut mettre (b - c) ou (c - b) en facteur. Etant de degré 3, il s'écrit donc, avec α réel :
On identifie immédiatement α à 1. Par suite :
➔ Pour en savoir plus :
Mémoire sur la résolutions des équations, par
Alexandre Vandermonde (version fr dès la page 59) :
http://www.17centurymaths.com/contents/lagrange/treatisenumeq/vandermondeoneqns.pdf
Notice sur l'élimination par Orly Terquem
(historique sur la résolution des systèmes d'équations)
a)
http://www.numdam.org/article/NAM_1842_1_1__125_0.pdf
b)
http://www.numdam.org/article/NAM_1846_1_5__153_1.pdf
Galoi's theory of algebraic equations, par Jean-Pierre Tignol (en anglais
sur Google books) :
http://books.google.com/books?id=hO6HYckIYxsC&printsec=frontcover&hl=fr#PPA153,M1
(Une très grande partie du livre est accessible. L'adresse
ci-dessus renvoie directement à Vandermonde, page 153).
Notion de faculté analytique par Auguste L. Crelle, sur Google livres (plus particulièrement pages 269 et suivantes) :
http://books.google.fr/booksid=wUPAAAAIAAJ
De la résolution algébrique de l'équation xp
- 1 = 0 lorsque p est premier, par M. Realis (Nouvelles Annales
mathématiques, 1843) :
https://books.google.fr/books?id=aQ0FAAAAQAAJ&pg=PA5&lpg=PA5&dq=xp -
1#v=onepage&q=xp - 1&f=false
Lagrange