ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Loi de Cauchy
(distribution de probabilités) »
loi continue
niveau Sup |
On considère un point M point placé aléatoirement sur le cercle (c) ci-dessus, supposé de rayon 1. Il est repéré par l'angle θ.
La demi droite [PM) coupe l'axe des abscisses en A d'abscisse x. L'abscisse de A est une variable aléatoire X.
On demande d'établir la loi de probabilité de X (densité).
Indications :
La distribution de θ est uniforme et la circonférence de (c) est 2π. Avec les notations de la figure ci-dessous, si T est la variable aléatoire associée, sa densité est alors 1/2π (1 sur 2π) et sa distribution de probabilité est régie par :
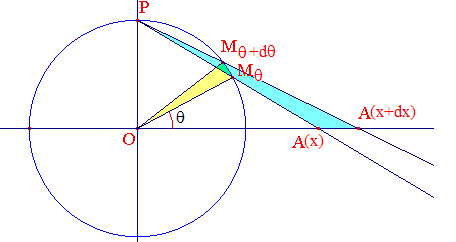
En se plaçant dans le triangle OMP, on constate que x = tan(π/4 + θ/2), donc :
θ/2 = Atan x - π/4
Par suite :
dθ = 2dx/(1 + x2)
D'où :
Prob(x < X < x + dx) = Prob(θ < T < θ + dθ) = 1/π × dx/(1 + x2).
X suit donc la loi de Cauchy de densité :
Une autre construction de densité, la loi exponentielle : ››››