ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

L'usage des fonctions complexes (comme pourrait l'indiquer leur nom...) n'est pas simple. Lors de la définition de telles fonctions, on rencontre généralement des difficultés au niveau de la détermination de l'image : non unicité, défaut de continuité. On parle de fonction multiforme s'opposant aux fonctions uniformes (qualificatif dû à Hermite) : unicité de l'image.

La définition de ces fonctions entraîna des débats houleux au 18è siècle entre les grands mathématiciens de l'époque comme Euler, Jean Bernoulli, Leibniz, d'Alembert. Elles ont permis de développer, avec Cauchy et Weierstrass la théorie des fonctions analytiques (fonctions développables en série entière).

Si la définition de la fonction carrée z → z² , de la fonction inverse z → 1/z ou de la fonction exponentielle z → e^z ne pose pas de problèmes majeurs, il n'en va pas de même, par exemple, avec les tentatives de définition des fonctions racine carrée et logarithme.

∗∗∗
a) En admettant la formule d'Euler et en dérivant cos x + i.sin x par rapport à x, montrer que la fonction dérivée de x → e^ix n'autre que x →  i.e^ix.
b) On pose z = x + iy et pour tout complexe z : exp(z) = e^x(cosy + i.siny). Vérifier que exp(z + z') = exp(z) x exp(z').

Définition en tant que série entière de l'exponentielle complexe : »

Si z est un nombre complexe, on peut l'écrire : z = r × e^{i(θ + 2kπ)} où r est le module de z et θ un argument de z, défini à 2kπprès. Lorsque k décrit Z, z reste inchangé. Les racines carrées de z dans C sont alors √r × e^{i(θ/2 + kπ)} avec k = 0 ou 1. On est en présence d'une fonction multiforme : deux images opposées. Laquelle choisir ?  

Problème a priori insoluble quel que soit le choix car nous travaillons ici dans C, assimilable à R² : supposons qu'un complexe z' décrive une boucle ne contenant pas l'origine, son argument "augmente" puis revient à sa valeur initiale après un tour complet :

Par contre, si, tel z sur le schéma ci-dessus, on décrit une boucle contenant O, alors son argument augmente de 2π : z reprend donc sa valeur initiale mais, "pendant ce temps là", l'argument de la racine carrée choisie verra son argument augmenter de π. Au final, on retombe sur l'autre détermination de la racine carrée ! On dit que l'origine est un point critique ou un point de branchement pour la fonction racine carrée : elle est une fonction multiforme autour de O.

La notion de surface de Riemann :   

Pour remédier à ce problème, Riemann imagine un artifice redéfinissant l'ensemble de définition des fonctions complexes : on parle aujourd'hui de surfaces de Riemann sur lesquelles ces fonctions redeviennent uniformes (nos fonctions usuelles : l'image est unique).

Voici, ci-dessous, une représentation de la surface de Riemann associée à la fonction racine carrée complexe due à Jean Bass dans son Cours de Mathématiques (» réf.2) :

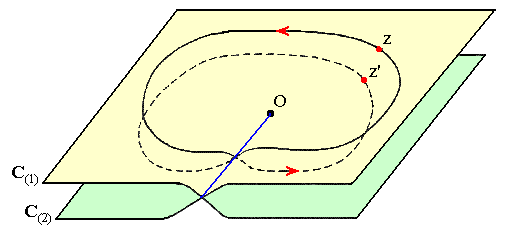
On "clone" le plan complexe que l'on représente par deux feuillets C₍₁₎ et C₍₂₎ reliés entre eux par le demi-axe positif, appelé coupure. L'origine O qui pose ici problème, est appelé point de branchement. Aucune boucle autour de O ne doit franchir cette coupure à moins de passer de C₍₁₎ à C₍₂₎ ou inversement. Dans ces conditions, z ne reprendra sa valeur initiale qu'au bout de 2 tours.

 !  L'origine du plan complexe n'est pas toujours la fautive ! Si vous cherchez à donner un sens à la racine carrée de la fonction z → z⁴ - 1, il vous faudra effectuer 4 coupures : les points de branchements seront 1, -1, i, -i.

Ayant fait le choix d'une détermination de la racine carrée, celle-ci devient uniforme sur la surface de Riemann, ce qui autorise alors la notation √z. Dans le plan ainsi coupé, cette fonction est cependant discontinue en tout point de la coupure.

Cette "astuce" de Riemann permet par exemple d'appliquer le théorème des résidus non utilisable dans C du fait de la discontinuité produite par toute rotation autour d'un point de branchement.

Ci-dessous : Une autre vision (à gauche) de la surface de Riemann associée à la racine carrée complexe, plus esthétique grâce à l'informatique. à droite un compromis fabrication maison : le complexe z tourne autour de O dans C₍₁₎; en butant sur la coupure, il plonge dans C₍₂₎, fait un tour complet et bute de nouveau sur la coupure dans C₍₂₎ : z refait surface dans C₍₁₎ pour revenir à son point d'origine au bout de 2 tours.

Si θ = Arg z (argument principal) est l'argument principal d'un complexe z de module r, on a :

z = r x e^iθ, mais aussi z = r x e^{i(θ + 2kπ)}

Si le logarithme du nombre complexe z est calqué sur le logarithme du cas réel par prolongation, il peut logiquement se définir par :

Log z = Log (r x e^iθ) =  ln r + iθ × ln e = ln r + iθ     où ln désigne le logarithme népérien

Mais on devra avoir aussi :

Log z = Log (r × e^{i(θ + 2kπ)}) =  ln r + iθ +2ikπ

Il s'agira donc d'une fonction multiforme. On conçoit que la surface de Riemann associée à Log z possède une infinité de feuillets s'interprétant comme une surface hélicoïdale :

En tant que fonction réciproque de la fonction exponentielle complexe, il s'agira d'être extrêmement prudent... : on obtient une fonction uniforme (image unique) en utilisant le logarithme principal et il ne s'agira pas de tourner autour de l'origine qui est, là encore, un point critique. D'où la nécessité de restreindre l'ensemble de définition de Log z à un plan coupé par une demi-droite arbitraire : l'usage est de choisir le demi axe négatif.

∗∗∗
1.  On définit le logarithme principal dans C^*par Log z = ln r + iθ avec θ = Arg z
a) Calculer Log(i) et log(-i); comparer Log z et Log z.              b) Comparer Log(z) et Log(-z)
Attention dans cette question :
les étourdis prendront conscience que θ dans Log z =  ln r + iθ n'est pas un argument de Log z mais sa partie imaginaire !

2.  Le plan complexe est maintenant coupé selon le demi-axe négatif. Pour tout z∈C - R^-, on pose Log z = ln r + iθ avec θ = Arg z.
a) Soit j la racine cubique de l'unité :  j =  [1;2π/3] = -1/2 + i√3/2. Montrer que Log j² ≠ 2Log j.
b) On pose z = x + iy et z' = x' + iy'. Montrer que si yy' < 0, alors Log(zz') = Log z + Log z'.
c) Soit a strictement négatif. On pose z = a + iy, y > 0, Arg z = θ et z ' = a + iy', y' < 0, Arg z = θ'. Calculer Log z - Log z'.
Déduire, en faisant tendre y et y' vers 0, que Log z ne se prolonge pas continûment à C^*.

On se place dans l'espace euclidien usuel, C étant assimilé au plan (P) = (xOy). Considérons la sphère unité Σ centrée en O, de rayon 1. Envoyons alors Σ sur C par projection stéréographique de pôle N, pôle nord de Σ, sur son plan équatorial (P), un concept remontant à Hipparque de Nicée. Par définition, l'image d'un point M de Σ autre que N est le point d'intersection de (NM) avec (P).

Le cercle unité de (P), équateur de Σ est invariant. Les points de l'hémisphère sud ont leur image sur le disque équatorial. N n'a pas d'image : elle est "rejetée à l'infini". L'argument d'un point à l'infini est indéfini, raison pour laquelle on identifie conventionnellement à un seul point l'ensemble des images rejetées à l'infini portées par les demi-droites [N,→ [ parallèles à (P). Ce point à l'infini est noté ∞. Il peut être défini par z → ∞ ⇔ |z| → ∞ ⇔ 1/z → 0.

On convient que k/0 = ∞ pour tout k non nul de C et que 1/∞ = 0.  Topologiquement, en choisissant comme voisinages du point à l'infini, les ensembles de la forme K'∪{∞} où K' est le complémentaire d'un compact de C, on démontre que C ∪ {∞}, ensemble appelé de nos jours sphère de Riemann, est homéomorphe à la sphère unité Σ et que cet ensemble, en tant qu'espace topologique, est compact (» réf.1).

 ➔  r décrivant R⁺- {0}, on peut choisir les ensembles K' en tant qu'ensembles de nombres complexes z de module strictement supérieur à r, complémentaires des disques fermés |z| ≤ r du plan complexe.

Compactifié d'Alexandrov : »

Expression analytique de la projection stéréographique de pôle N :   

Avec les notations de l'illustration ci-dessus, on s'intéresse à la projection stéréographique de pôle N appliquant la sphère Σ sur son plan équatorial (P) identifié à C : M → z (M ≠ N), z désignant indifféremment le complexe x + iy et son image dans le plan complexe. La colinéarité de N, M et z permet d'assurer l'existence d'un réel k tel que Nz = kNM et, en termes de coordonnées, outre M(u,v,w) se projetant sur (P) en m =  u + iv, nous avons N(0,0,1), z(x,y,0), ce qui fournit x = ku, y = kv et -1 = k(w - 1). Cette dernière égalité fournit k = 1/(1 - w). Finalement :

z = (u + iv)/(1 - w)

Inversement :   

Si z ∈ C, en posant k = 1 + | z |², on a z → M(u,v,w) ∈ S₂ avec u = (z + z)/k, v = (z - z)/k, et w = (| z |² - 1)/k.

Expression analytique de la projection stéréographique de pôle S :    

En envisageant la projection stéréographique de pôle S, symétrique de N par rapport à (P), un calcul similaire conduit à Sz' = kSM avec S(0,0,-1), donc à z' = (u + iv)/(1 + w). Mais cette expression calquée sur la précédente ne doit pas être utilisée dans la mesure où l'on tient compte, en cartographie, d'angles orientés (» alinéa suivant) : dans cette symétrie, l'argument de m est changé en son opposé; autrement dit, m est changé en son conjugué :

z' = (u - iv)/(1 - w)

 ➔  Remarques :   

a) z × z' = (u² + v²)/(1 - w²); le point M(u,v,w) de S₂ vérifie u² + v² + w² = 1; par suite z × z' = 1. C'est dire que :

z' = 1/z pour tout M non situé sur l'axe (NS)

Surfaces de Riemann, cartes & atlas : »

b) Pour tout M(u,v,w) distinct de N et S, |z|² = |z'|² = (1 + w)/(1 - w)

Notons λ et φ les longitudes et latitude de M sur Σ⁺ assimilée à notre planète (hémisphère nord plus précisément). On a :

• ON = OM = 1, le triangle ONM est isocèle et ^NOM = π/2 - φ , on en déduit :
  ^ONM = ^OMN = π/4 + φ/2.

• x = Oz.cosλ et Oz = tan^ONM = tan(π/4 + φ/2), d'où x = tan(π/4 + φ/2).cosλ.

• De la même façon : y = tan(π/4 + φ/2).sinλ.

On est donc amené à :

z = x + iy = tan(π/4 + φ/2).e^iλ

La projection stéréographique est une transformation conforme (elle conserve les angles) et, pour tout z de C \ R^-, le logarithme népérien complexe défini par Log z = ln r + iθ avec θ = Arg z (argument principal de z) est holomorphe, c'est donc également une transformation conforme. Appliquons alors la fonction k. Log ( k constante non nulle) à z = tan(π/4 + φ/2).e^iλ, on obtient :

x = k.Log |tan(π/4 + φ/2)|   , y = k.λ         (f)

• si φ est constante (latitude = c^te, on décrit un parallèle de la Terre) alors
  x = c^te et sa représentation est une droite parallèle à (Oy).

• si λ est constante (longitude = c^te, on décrit un méridien de la Terre) alors
  y = c^te et sa représentation est une droite parallèle à (Ox).

Ce résultat montre que les parallèles et les méridiens sont représentés par un maillage de droites perpendiculaires. Dérivons x par rapport à φ dans la formule (f) ci-dessus : dx/dφ = k/cosφ  (» primitive de 1/cosx) : on retrouve le principe de correction de Mercator  pour l'espacement entre les projections des parallèles (cercles de même latitude). Ce qui prouve que la projection cylindrique de Mercator est conforme.

Loxodromie et orthodromie : »           » Jacqueline Lelong-Ferrand  

Une surface de Riemann se définit aujourd'hui comme un espace topologique X localement homéomorphe au plan complexe pour lequel les homéomorphismes σ_i appliquant les ouverts U_i de X sur ceux de C définis ci-dessous vérifient une condition d'holomorphie :

• les couples (U_i ,σ_i ) sont appelés cartes;

• les composés σ_i  o σ_j^-1 : C → C sont appelés changements de cartes ou encore ou fonctions de transitions;

• La restriction de tout σ_i  o σ_j^-1  à une intersection non vide U_i ∩U_i est holomorphe (analytique);
  le passage d'un feuillet à l'autre se fait dans des conditions optimales !

• Un recouvrement de X par des cartes est un atlas.

On voit encore ici le lien "cartographique" déjà rencontré ci-dessus avec la projection stéréographique : on peut dire que les cartes permettent de "lire" dans C ce qui "se passe" sur la surface de Riemann, son image homéomorphe. Vue ainsi, la sphère de Riemann apparaît comme un cas trivial de surface de Riemann avec les deux cartes (C, id : z → z) et (C^* ∪ {∞}, z → 1/z).

De façon encore plus abstraite, une surface de Riemann s'interprète en tant que variété analytique de dimension  complexe 1 dont l'espace topologique sous-jacent est séparé  :

Variétés différentielles et surfaces de Riemann : »            » Théorème de Riemann-Roch        » Mirzakhani

 ➔   Pour en savoir plus :

1. Calcul différentiel complexe, par Daniel Leborgne - Que sais-je n°2560, Presses Universitaires de France.

2. Cours de Mathématiques, tome2 - Fonctions analytiques, Jean Bass - Éd. Masson & Cie - Paris, 1964.

3. Cours de Mathématiques - 2, Analyse, J.M. Arnaudiès et H. Fraysse, Éd. Dunod Université - Paris, 1989

4. La Géométrie et les Imaginaires, par Émile Borel et Robert Deltheil - Éd. Albin Michel - Paris, 1931

5. Géométrie différentielle élémentaire (363 pages), par Frédéric Paulin, univ. Paris-sud/Saclay :
   a) http://www.math.u-psud.fr/~paulin/notescours/cours_geodiff.pdf ou bien :
   b) https://www.imo.universite-paris-saclay.fr/~paulin/notescours/cours_geodiff.pdf

6. Introduction à la géométrie hyperbolique et aux surfaces de Riemann, par Ricardo Sá Earp & Eric Toubiana