ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
LAGRANGE Joseph Louis, Comte de-, français, 1736-1813Mécanique céleste | Théorie des fonctions | Théorème des accroissements finis | Théorème de la moyenne Équations algébriques | Équation de Lagrange | Interpolation | Arithmétique | Formes quadratiques |
Né
à Turin (Torino), d'origine franco-italienne (son grand-père, officier français,
installé à Turin dans la garde du duc de Savoie
Charles-Emmanuel II, avait épousé une italienne de la famille Conti),
Joseph-Louis fut le cadet d'une fratrie de onze enfants dont les dix premiers
moururent encore enfants.
Brillant élève, il s'intéresse très tôt aux mathématiques, en dévorant les travaux de Newton sur le calcul différentiel et intégral, et à l'astronomie en découvrant ceux de Halley. à 19 ans, on lui confie un poste d'enseignement des mathématiques à l'École d'artillerie de Turin. à 23 ans (on est en 1759), il se fit brillamment connaître par la publication de ses Actes de la société privée où il aborde des sujets de physique mathématique : isopérimètres, surfaces minimales (calcul des variations), acoustique, hydrodynamique, point de départ de sa Mécanique analytique. Le calcul différentiel devient pour la première fois un des outils du calcul des probabilités.
Histoire (compliquée) du Royaume de Piémont-Sardaigne sur Wikipédia : »
Encouragé par d'Alembert avec lequel il entretint de nombreuses correspondances (jusqu'à son arrivée à Paris en 1787), il fut à l'origine, en la même année 1759, de l'Académie des sciences de Turin qui deviendra celle du Royaume de Sardaigne en 1783. Admiratif de ses travaux, Euler le fait venir à Berlin (1766) en tant que mathématicien à la cour de Frédéric Legrand et élire à l'Académie des sciences de Berlin. Il y restera 20 ans et succédera à Euler à la présidence de l'Académie des sciences.
Frédéric le Grand meurt en 1786. Lagrange s'installe à Paris l'année suivante à l'invitation de Louis XVI. Membre de diverses commissions scientifiques, comme celle du système métrique, il traverse la Révolution de 1789 sans encombres, ce qui ne fut pas le cas de son ami, l'éminent chimiste Lavoisier également membre de ces commissions. à Berlin, Lagrange avait épousé une parente éloignée de sa famille turinoise qu'il perdit suite à une longue maladie. En 1792, il épousa la jeune Adélaïde, fille de son ami astronome Pierre Charles Lemonnier (1715-1799) et qui l'accompagnera jusqu'à sa mort. Membre fondateur du bureau des longitudes, savant universel, ce brillant mathématicien, physicien et astronome, expert en mécanique céleste, fut anobli par Napoléon et inhumé au Panthéon.
i Antoine Laurent de Lavoisier (1743-1794) est considéré comme le père de la chimie moderne. Il est à l'origine de la loi de conservation de la masse et des éléments chimiques dans les transformations de la matière (principe de Lavoisier) résumée en « rien ne se perd rien ne se crée, tout se transforme ». Il découvrit la composition de l'eau (H2O) et établit le rôle fondamental de l'oxygène (on lui doit cette appellation, 1783). Peu avant la révolution, Lavoisier fut aussi Fermier général, en quelque sorte percepteur des impôts, un emploi mal perçu à cette époque. Arrêté en 1793, il ne put échapper à la guillotine.
La contribution de l'illustre homme de sciences en mathématiques, astronomie et sciences physiques est colossale et comparable à celle de son ami Leonhard Euler. En mathématiques, on peut citer :
Les équations différentielles et aux dérivées partielles ;
La résolution des équations algébriques, les formes quadratiques et l'arithmétique;
Concernant ce dernier et fondamental sujet de mathématiques appliquées (mécanique rationnelle), l'appellation est due à Euler (en latin, Calculi variationum), Lagrange parlait de méthode des variations. Initiée par les Bernoulli et Euler, il la développa dès 1755 parallèlement aux travaux de ce dernier en une branche maîtresse et à part entière du calcul différentiel et intégral (» réf. 10a) qui sera l'outil principal de l'application du principe de moindre action, cher à Maupertuis.
Dans le même ordre d'idées et l'étude des surfaces algébriques, Lagrange s'intéresse aux surfaces minimales (pour signifier qu'une portion d'une telle surface délimitée par une courbe fermée présente une aire minimale. Pour qu'il en soit ainsi, il montre que leurs courbures moyennes doivent être nulles en tout point, ce qui le conduit au résultat suivant :
Si z = f(x,y) désigne l'équation d'une surface minimale de R3, (x,y) décrivant un domaine borné D de R2, notons :
z'x = ∂z/∂x , z'y = ∂z/∂y , z''xy = ∂2z/∂x∂y , z''xx = ∂2z/∂x2 , z''yy = ∂2z/∂y2
les dérivées partielles de z des premier et second ordre par rapport à x et y. Lagrange établit que z vérifie l'équation aux dérivées partielles du second ordre :
Identité que l'on vérifiera facilement avec l'équation de la surface de Scherk : z = ln(cos(x)) - ln(cos(y)).
Multiplicateur de Lagrange : » » Meusnier , Plateau , Bernstein
La Mécanique analytique (1788, » réf. 2), magistrale synthèse de ses recherches, où explique les perturbations des orbites planétaires en appliquant à la théorie newtonienne les principes mathématiques du calcul des variations. Depuis la parution de son ouvrage, on parle de lagrangien et de systèmes lagrangiens, pour exprimer des relations fondamentales régissant le mouvement des systèmes mécaniques célestes ou non.
Équation de Kepler : »
Arithmétique et formes quadratiques : équations diophantiennes, étude de l'équation de Pell (» réf. 8) le conduisant à la notion de forme quadratique (Recherches d'arithmétique, à partir de 1775) dont la théorie fut développée par Gauss, Legendre, Hermite, et bien d'autres avant d'être parachevée par Siegel au 20è siècle.
Développements en série (formule de Taylor) : Lagrange reconstruit l'analyse en s'intéressant tout particulièrement aux fonctions développables en série et aux fonctions de plusieurs variables dans sa Théorie des fonctions analytiques (1797, » ref. ).
» Condorcet , Weierstrass
|
La mécanique céleste, le problème des trois corps, la théorie des systèmes dynamiques : |
Lagrange étudia tout particulièrement l'orbite lunaire du système céleste Terre-Lune-Soleil et expliquera ses perturbations, appelées librations, ce qui lui valut le prix de l'Académie des sciences (1764). La plus étonnante de ces perturbations est le fait que la Lune présente toujours à la Terre la même face car il s'est établi entre notre planète et son satellite un équilibre remarquable : la Lune tourne autour de la Terre dans exactement le même temps qu'elle tourne sur elle-même.
Le problème des n corps :
L'étude
du trio
Terre-Lune-Soleil est un cas concret d'un problème fameux, dont
Euler
et d'Alembert sont à la source vers 1740. En 1772,
Lagrange apporte une solution partielle qui lui vaut (encore) le prix de
l'Académie des sciences (Mécanique analytique, V.12 des
Œuvres complètes, »
réf. 11).
Dénommé, dans le cas général, problème des n corps, il s'agit de déterminer les trajectoires (orbites) de n corps célestes en interactions dans l'espace. Newton, par sa théorie de la gravitation universelle, apporta auparavant la solution au cas n = 2 (conique).
Pour n = 3, le problème devient beaucoup plus ardu : par exemple, dans le cadre du trio Terre-Lune-Soleil, en convenant que ce dernier est fixe et que la Terre décrit une parfaite ellipse selon les lois de Kepler, l'orbite lunaire autour de la Terre subit des perturbations de par les forces gravitationnelles induites par le Soleil. Son étude conduit à un système de 3n = 9 équations aux dérivées partielles du second ordre. Les outils mathématiques de l'époque ne permettent pas sa résolution.
En France, d'Alembert (1749), Clairaut et Euler (la même année), Condorcet, Laplace et Delaunay apportèrent des solutions partielles approchées (méthode d'approximations successives, » réf.13). En recherchant les solutions par le biais de séries convergentes, une avancée dans l'obtention d'une solution exacte est présentée par Poincaré en 1889. Il confirme, comme le soupçonnaient ses prédécesseurs, que le système différentiel régissant le problème n'est pas intégrable en ce sens que les coordonnées de la Lune (la Terre étant prise comme origine) ne peuvent pas être calculées par quadratures.
Considéré comme un des plus difficiles problèmes mathématiques, le problème des trois corps a été résolu en 1909 par l'astronome et mathématicien finlandais Karl Sundman en recherchant les solutions sous formes de séries dans le prolongement des travaux de Poincaré. Entre 1919 et 1922, le français Jean Chazy confirme et affine les résultats de Sundman.
La théorie des systèmes dynamiques :
Le problème des trois corps fut, avec les premiers modèles mathématiques de systèmes planétaires initiés par Aristarque, en passant par la mécanique de Galilée, les mécaniques célestes de Kepler, Laplace ou Newton, à l'origine de la théorie des systèmes dynamiques consistant à étudier, en fonction du temps le comportement d'un système régi par des systèmes d'équations différentielles. Avec Smale (médaille Fields, 1966) et Thom, cette théorie devient une branche de la topologie différentielle.
|
Théorie des fonctions, calcul intégral, notations nouvelles : |
Les principaux traités mathématiques de Lagrange résident dans la Théorie des fonctions analytiques (1797, » réf.5) où il cherche à définir les fonctions et leurs dérivées successives par leur développement en série au voisinage d'un point, un sujet fondamental que Weierstrass complétera (1886) en mettant en place le nouveau concept de convergence uniforme.
Dans cet ouvrage, Lagrange simplifia les notations fonctionnelles en introduisant :
La notation f(x) pour une fonction numérique et
f
'(x) pour la
fonction dérivée de f, dite
première fonction dérivée, ainsi que
f'', appelée
seconde fonction dérivée,
f''', etc.
Si y est fonction de x, Lagrange propose la notation simplifiée y', y" pour les dérivées première, seconde (dérivée de y'), etc.
» Newton , Arbogast Fonction dérivée selon d'Alembert : »
Cas des dérivées partielles (fonction de plusieurs variables) : »
Eu égard, aux notations précédentes,
Lagrange appelle
fonction primitive une fonction f dont la
dérivée est
f' et
donne ainsi un sens à ce qui deviendra le concept de primitive
de f sur un intervalle
J : une fonction F telle que pour tout x de J, F'(x) = f(x).
Et cette primitive est définie à une constante additive près.
➔ Par primitif, on entendait à l'époque -indépendamment de tout sens mathématique- ce qui n'est dérivé d'aucun autre et par dérivé (du latin rivus = ruisseau) celui qui provient d'un autre appelé primitif. On tourne un peu en rond, mais c'est clair... Noter que le substantif primitive (d'une fonction) ne prendra sa place définitive qu'au 20è siècle (en 1930 selon Le Robert, dictionnaire historique de la langue française) car on lui préférait jusqu'alors le terme intégrale proposé par Jean Bernoulli et l'Hospital.
Avec les notations ci-dessus, si [a,b]⊂J, on a la notation de Fourier pour l'intégrale définie :
Intégrale selon Riemann : » Intégrale selon Cauchy : » Intégrale définie et intégrale généralisée : »
∗∗∗
1. Déterminer la (les) fonction(s) numérique(s) vérifiant xf(x) + f(1 - x) = x2 (inspiré de 300 problèmes, IREM de Lyon, 1991). ☼
2.
niveau Ter : a)
Calculer sin x /(1 - cos
x) - sin x/(1 + cos x).
b)
En déduire :
➔ Le calcul de cette primitive s'effectuera aisément en posant t = tan(x/2); auquel cas dx = 2dt/(1 + t2), ce qui conduit à ∫dt/t
c) Par un artifice semblable, montrer que :
➔ On peut encore poser t = tan(x/2) ou se ramener à la primitive de 1/sinx en posant t = π/2 - x.
i On vient de calculer là les primitives des fonctions trigonométriques sec (sécante, inverse du cosinus) et cosec (cosécante, inverse du sinus).
d) Utiliser un de ces deux résultats pour calculer l'intégrale :
Rép : ln
3
3. » Intégration par parties Calculs d'intégrales
4. » calcul d'intégrales & primitives diverses avec indications de solution (niveau sup).
♦ Principe de Lagrange (sens de variation d'une fonction numérique par usage de sa dérivée) :
Utilisant la formule des accroissements finis (» ci-dessous), Lagrange lie le sens de variation d'une fonction au signe de sa dérivée. C'est aujourd'hui l'un des théorèmes fondamentaux dans l'étude des fonctions numériques au lycée :
Si f est dérivable sur l'intervalle ]a,b[, alors f est
respectivement croissante, constante ou décroissante
suivant que f ' est positive, nulle
ou négative sur cet intervalle.
Dans les cas usuels où la fonction dérivée f
' est continue sur l'intervalle ]a,b[, l'usage des théorèmes de
Bolzano et de Rolle permettent d'étudier
facilement le sens de variation d'une fonction : un zéro isolé xo
de f'
atteste la présence d'un point remarquable de la courbe :
maximum local en un point xo : au voisinage de ce point, on a f(x) ≤ f(xo);
minimum local en un point xo : au voisinage de ce point, on a f(x) ≥ f(xo);
point
d'inflexion
en un point xo :
f' s'annule en
xo sans changer de signe.
Des cas particuliers peuvent avoir lieu, comme un minimum en un point alors que f n'est pas dérivable en ce point. C'est le cas de la fonction x → √|x|, racine carrée de la valeur absolue de x :
∗∗∗
Déterminer les fonctions numériques dérivables
vérifiant f(x + y) = f(x) + 2xy + f(y) Rép
:
ici
En savoir plus sur les extremums et l'inflexion : » Tangente à une courbe : » » D'Alembert
∗∗∗
Quelques exemples "concrets" niveau lycée
| Tente bien ventilée fonction trinôme à "maximiser" |
| Un problème bestial... minimum d'un trinôme du second degré |
| Puissance d'un moteur électrique trinôme 2ème degré |
| Le 8 du jardinier aire maximale d'un parterre, secteurs circulaires et second degré |
| Résistor et puissance dissipée fonction rationnelle x/(2x + 1)2 |
| Résistance d'une poutre étude d'un binôme du 3ème degré |
| Cuves maximales (diverses variantes) x(3 - 2x)2 , πx2 - 8/x, ... |
| Tétraèdre de volume maximal inscrit dans une sphère se ramène à l'étude d'une cubique |
| Le puits et la maison fonction irrationnelle à minimiser |
| Bouée d'amarrage fonction irrationnelle |
| La Jeep et le lac fonction trigonométrique à minimiser |
| Échelles croisées fonction irrationnelle |
| Dérivée non continue : étude de la fonction f : x → x2cos(1/x) , |
♦ Formule des accroissements finis, également dite Formule de Lagrange :
Si f est une fonction numérique continue
sur l'intervalle fermé [a,b] et dérivable sur ]a,b[,
il existe un réel c de ]a,b[ tel que f(b) - f(a) = (b - a)f
'(c)
La formule fournit ce que l'on appelle l'accroissement de f entre a et b. Elle est une conséquence du théorème de Rolle et peut également s'écrire :
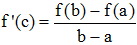
faisant apparaître f '(c) comme un taux d'accroissement de f sur [a,b]. Ou encore, comme souvent rencontré, en posant h = b - a et en remarquant que c, compris entre a et b, peut s'écrire a + θh avec 0 < θ < 1 :
f(a + h) - f(a) = hf '(a + θh)
i Par accroissements finis, on entend un accroissement Δx = x - y représentant une quantité finie, immédiatement calculable sans passage à une limite et s'opposant à une quantité dx infinitésimale. » différences finies.
La formule des accroissements finis est à distinguer de l'inégalité des accroissements finis :
♦ Inégalité des accroissements finis :
Soit f une fonction continue sur l'intervalle
[a,b] et dérivable sur son intérieur ]a,b[, de fonction dérivée f'
bornée vérifiant m ≤
f
'(x) ≤ M, alors pour
tout couple (x,y) de [a,b], on a :
∗∗∗
On pose h(x) = sin(x)/x, x non nul. Montrer, sans étudier
h, que l'on a -1 ≤ h(x) ≤ +1
Indication :
utiliser l'inégalité des acc. finis pour f(x) = sin(x).
Application (exercice niveau TerS/SUP) : »
Formules de la moyenne (intégrale d'un produit) : »
| Théorème de la moyenne et valeur moyenne d'une fonction : |
Si f' joue le
rôle de f dans la formule des accroissements finis, F désignant une primitive
de f, on a F(b) - F(a) = (b - a)f(c). La différence F(b) - F(a) n'est autre que
l'intégrale de f sur [a,b]. On peut alors énoncer le
théorème de la moyenne :
Si f est une fonction numérique continue sur l'intervalle [a,b], il existe c dans ]a,b[ tel que :
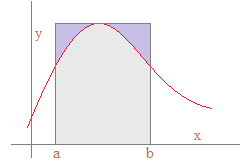De
cette égalité, on peut déduire un résultat intéressant dans les problèmes
de majoration (évident graphiquement dans le cas d'une fonction positive sur
l'intervalle d'intégration en interprétant l'intégrale comme la mesure
de l'aire sous la courbe) :
Bonnet et le second théorème de la moyenne : »
Valeur moyenne de f sur [a,b] :
➔ Avec les notations précédentes, le nombre f(c) :
est appelé moyenne de f sur l'intervalle [a,b].
∗∗∗
En se ramenant à une
somme de Riemann, calculer la limite pour n
infini de (1 +
√2 +
√3 + ...
√n) / n√n.
Rép : il s'agit de
l'intégrale sur [0,1] de la fonction x →
√x, soit 2/3.
Cas des fonctions harmoniques : »
|
La notation moderne des suites numériques : |
On doit également à Lagrange la notation indicée, dite aussi indicielle, (un) pour désigner le terme de rang n d'une suite numérique.
La suite de nombres 1, 3, 5, 7 , ... des entiers impairs est une suite numérique (un) définie pour tout entier n, par un = 2n + 1. On a uo = 1, u1 = 3, u2 = 5, u3 = 7... On peut aussi définir la même suite de nombres par vn = 2n - 1 à condition de définir la suite (vn) pour n ≥ 1 : v1 = 1, v2 = 3, v3 = 5, v4 = 7, ...
∗∗∗
Exercices sur les suites (et séries) dans Chronomath :
niveau 1ère/Ter
|
niveau TerS/SUP
| Méthode d'interpolation polynomiale de Lagrange : |
Soit f une fonction numérique. Interpoler f par un polynôme sur un intervalle [a,b], c'est choisir une subdivision, non nécessairement régulière :
et rechercher un polynôme P de degré n, dit polynôme d'interpolation, qui coïncide avec f en chaque point Mi(xi , yi) , yi = f(xi). Lorsque la fonction f est seulement connue par un ensemble de points (nuage), comme le cas se rencontre couramment en statistique, interpoler f sur l'intervalle [a,b] par une fonction g de type donné (polynomial, logarithmique, exponentielle, trigonométrique, ...) consiste à calculer les paramètres de g afin d'approcher au mieux les valeurs connues des yi = f(xi).
➔ On parle d'interpolation linéaire lorsque le polynôme est de degré 1 : l'arc de courbe est remplacé par un segment. Au lieu d'interpolation, on utilise plus volontiers le terme statistique de régression.
En savoir plus sur l'interpolation et les méthodes de régression : »
| La résolution des équations algébriques : |
Lagrange
s'est fortement intéressé aux équations
algébriques. Lors de son séjour à Berlin, il publie ses
Réflexions sur la résolution algébrique des équations (1772). Pour
résoudre l'équation du quatrième degré,
Ferrari
utilisa une équation auxiliaire de degré 3.
Lagrange prouve qu'au delà du quatrième degré, l'équation auxiliaire est de degré supérieur ! De nouvelles méthodes s'imposaient donc. C'est ainsi qu'il perçoit tout l'intérêt des fonctions symétriques des racines, déjà remarquées par Viète et Girard, et que Gauss, Cauchy, et enfin Abel et Galois utiliseront pour clore le problème de la résolution par radicaux de ces équations :
Considérons l'équation :
xn + a1xn-1 + a2xn-2 + … + an-1x + an = 0.
Selon le théorème fondamental de l'algèbre, cette équation admet n solutions xi réelles ou complexes, éventuellement multiples, Lagrange montre que (-1)kak = Σpk , somme de tous les produits possibles pk des solutions xi pris k à k. Par exemple, pour :
Lagrange complètera son étude des équations numériques en 1798 : Traité de la résolution des équations numériques de tous les degrés où il expose également des méthodes de résolution approchée. Sa dernière édition date de 1808.
Méthode des sécantes de Lagrange :
Également dite par interpolation linéaire, il s'agit d'une méthode algorithmique de résolution approchée des équations numériques où l'arc de courbe AB , "traversant" l'axe des abscisses en le zéro cherché, est remplacé par le segment [AB] :
Cette méthode de résolution est une méthode de fausse position, en latin regula falsi :
| Théorème de Lagrange sur les zéros d'un polynôme : |
Si P est un polynôme à coefficients réels ai, alors un zéro de P ne peut excéder Max(1+|ai|)
| Étude des formes quadratiques : |
Lagrange sera le premier, avant Gauss, à s'atteler au problème de la réduction des formes quadratiques (1767), ce qui le conduira à la résolution des équations du second degré à deux inconnues du type :
ax2 + bxy + cy2 = k
équation liée à celle de Pell, difficile équation en nombres entiers de la forme x2 - Ay2 = ±1 où A n'est pas un carré parfait, qu'il résout (» réf. 7) en développant la théorie des fractions continues déjà bien avancée grâce aux travaux de Aryabhata et de Chuquet.
|
Travaux en arithmétique : |
Dans ces travaux, Lagrange parle implicitement de groupe fini et de sous-groupe. Il énonça et prouva (1770) avant Cauchy cet important résultat :
Théorème :
Dans un groupe fini E d'ordre n (c'est à dire ayant n éléments), si k est l'ordre d'un sous-groupe F de E, alors k divise n.
Groupes finis et preuve de ce théorème : »
Théorème des quatre carrés (1770) :
Lagrange prouve une conjecture de Bachet de Méziriac, également énoncée (et élargie) par Waring et que Fermat démontra partiellement en son temps au moyen des nombres polygonaux de Nicomaque de Gérase :
Sa preuve sera simplifiée par Euler en 1777 et encore par Legendre et Gauss. Par exemple :
Théorème de Gauss (3 carrés) : » Programmation du théorème des 4 carrés : » Somme de 2 ou 3 cubes : »
Le théorème de Wilson-Lagrange (1773) :
Lagrange démontra le théorème connu aujourd'hui sous le nom de théorème de Wilson :
Le nombre (p - 1)! + 1 est divisible par l'entier p si et seulement si p est premier
Énoncé en 1770 par Wilson et utilisé auparavant sans démonstration par Waring son professeur à Cambridge, c'est alors la première preuve ce résultat (» réf.2b). On en trouvera la preuve au moyen des congruences à la page consacrée à Wilson.
|
Identité de Lagrange : |
Elle transforme un produit de carrés en une somme de carrés :
Par exemple : (x2 + y2)(x'2 + y'2) = (xx' + yy')2 + (xy' - x'y)2
∗∗∗
Application : Cosinus
directeurs d'une droite de l'espace euclidien
| Théorème d'inversion de Lagrange : |
Soit z une fonction de la variable y définie implicitement sous la forme z = y + k.f(z) où k désigne un paramètre (la fonction f dépend ainsi de y par l'intermédiaire de z). Lagrange affirme (sans trop de précautions ?) que toute fonction F de z peut être développée en série entière de puissances de y :
Ce résultat voit son application dans la résolution de l'équation de Kepler m = ε - e.sin ε.
» Taylor
|
Équation différentielle de Lagrange : |
Il s'agit de l'équation différentielle du premier degré de la forme :
y = x.f(y') + g(y')
Dérivons puis posons y' = z :
z = f(z) + [xf '(z) + g'(z)].z' , z' = dz/dx
Remplaçons z' par dz/dx, multiplions par dx et divisons par dz :
[z - f(z)].dx/dz - x.f '(z) - g'(z) = 0
C'est une équation linéaire d'inconnue x de variable z. On trouvera x en fonction de z et au moyen de l'équation initiale, qui s'écrit y = xf(z) + g(z), on cherchera à éliminer z afin d'obtenir la solution générale sous la forme F(x,y) = 0.
Cas particulier, équation de Clairaut : »
➔ Pour en savoir plus :
Wilson
