
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Nom de la fonction : logarithme népérien » Neper
Notation : Log, et plutôt de nos jours : ln, (logarithme népérien)
Etymologie : du grec logos =
science, logique, raison et arithmos = nombre
»
Neper.
Huygens
forgea logarithmique, népérien est dû à Euler.
Ensemble de définition : R+* = ]0 ,+∞[
Périodique : non.
Fonction dérivée : (ln x)' = 1/x.
Fonction primitive : x → xln x - x (en intégrant par parties)
Fonctions primitives de x → (ln x)n : on peut les obtenir par la récurrence Ln(x) = x(lnx)n - Ln-1(x)
Nom de la courbe associée : pas de nom spécifique (courbe logarithmique)
Définitions possibles : elles sont nombreuses comme, par exemple, celle consistant à l'étudier comme réciproque de la fonction exponentielle x → ex. La plus "fonctionnelle" est celle de Euler :
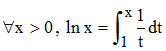
Pour x ≥ 1, ln x apparaît ainsi comme la mesure de l'aire grisée ci-dessous et pour 0 < x ≤ 1, ln x peut s'écrire :

C'est donc un nombre négatif que l'on peut encore interpréter comme la mesure algébrique (négative) de l'aire coloriée en vert, relative à la fonction x → -1/x :

Homographies, hyperbole : »

Le nombre e, base
des logarithmes népériens :
»
Calcul d'un encadrement élémentaire de e :
»
Limites usuelles :
|
fonctions |
x → 0+ |
x → +∞ |
|
ln(x) |
-∞ |
+∞ |
|
xln(x) |
0- |
+∞ |
|
ln(x)/x |
-∞ |
0+ |
∗∗∗
Appliquer une des limites ci-dessus afin de prouver
que x3/(ln x)2
est infini pour x infini positif.
Indications :
voir par ici...
Propriétés fondamentales :
ln(1) = 0; ln(e) = 1. » le nombre e, base des logarithmes népériens
ln(ab) = ln a + ln b a règle de dérivation des fonctions composées permet de montrer que f(x) = ln(ax) - ln a - ln x est constante. Or f(1) = 0, donc pour tout a et b strictement positifs, ln(ab) = ln a + ln b.
ln(1/x) = - ln x : ln(x/x) = ln 1 = 0 = ln (x × 1/x) = ln x + ln(1/x).
ln(a/b) = ln(a) - ln b car a/b = a × 1/b.
Applications :
La fonction logarithmique intervient dans toutes les branches de l'analyse, en symbiose avec la fonction exponentielle eu égard à l'équivalence :
Approches des fonction exponentielle et logarithmique : »
Tout phénomène logarithmique est lié à la fonction exponentielle (et réciproquement...). Si les courbes exponentielle et logarithmique sont tracées dans un même repère orthonormé, elles sont symétriques par rapport à la 1-ère bissectrice du repère d'équation y = x : c'est un résultat général pour deux courbes représentatives de deux fonctions réciproques l'une de l'autre.
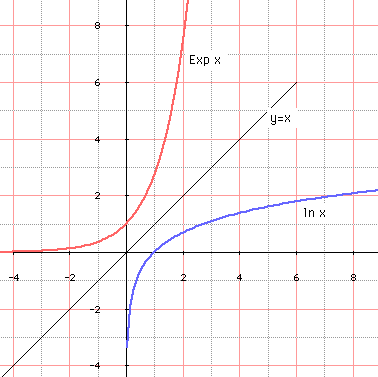
Comme domaine privilégié de ces fonctions logarithmiques et exponentielles, on peut citer l'électricité et l'électronique, la radioactivité, les statistiques et le calcul des probabilités (loi normale), la thermodynamique, les phénomènes vibratoires de type oscillatoire amorti d'équations de la forme a.e-ktcos(ωt + Φ), la cinétique des gaz, ...
∗∗∗
1. Calculer les primitives de x → 1/(1 - x2)
2. Etudier le
sens de variation de la fonction définie par x > 0, f(x) = 2x2
- lnx.
Indications : f '(x) = 4x - 1/x
est du signe de 4x2 - 1 = (2x + 1)(2x - 1). Or x > 0, par suite f '(x) est du
signe de 2x - 1.
3. Déterminer l'ensemble de définition de la fonction définie
pour x réel par
f(x) = -x.lnx -
(x - 1).ln(x - 1).
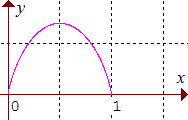
Étudier brièvement ses
variations en remarquant que la droite d'équation x = 1/2 est un axe de symétrie
de sa courbe représentative
dans un repère orthogonal. En déduire que si a et b
sont positifs vérifiant a + b = 1, alors : a.ln(1/a) + b.ln(1/b)
≤ ln2.
Lorsque le nombre a est positif, considérons les fonctions
x → ax , x réel
Le cas trivial a = 1 est proscrit. Le nombre a est appelé base : il s'agit des fonctions exponentielles de base a. Lorsqu'on parle de la fonction exponentielle (tout court, sans préciser la base), il s'agira de la fonction x → ex, que l'on peut aussi qualifier de fonction exponentielle de base e.
Les logarithmes de base a, notés loga furent définis par Euler au moyen de l'équivalence :
y = ax ⇔ logay = x.
Par suite, les études des fonctions exponentielle et logarithme de base a ( a > 0, a distinct de 1) peuvent se déduire facilement de celles de base e.

Lorsque a < 1, le sens de variation s'inverse (les fonctions associées sont décroissantes). Le logarithme de base 10 eut ses années de gloire par l'usage des tables de logarithmes et des règles à calcul jusqu'à l'apparition des calculatrices électroniques.
Neper, logarithmes de base a, logarithme décimal : »