ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 HERMITE Charles,
français, 1822-1901» matrice orthogonale, adjointe (transconjuguée), hermitienne |
Après
des études secondaires à Nancy et Paris (collège Henri IV) et ses classes
préparatoires au lycée Louis-le-Grand, Charles Hermite entre à Polytechnique en
1842. Étudiant brillant, il se fit connaître par ses correspondances avec
Jacobi à propos des
intégrales
abéliennes.
Ce grand mathématicien français, polytechnicien, ami de Cauchy, fut professeur à l'École Polytechnique (1869) et à la faculté des sciences de Paris. Il sera élu à l'Académie des sciences en 1856.
Ses travaux portent essentiellement sur la théorie des nombres et la théorie des fonctions elliptiques suite aux travaux de Jacobi. C'est ainsi que Hermite donna le premier (1858) une méthode de résolution de l'équation du 5e degré (dont on sait qu'elle n'est pas résoluble par radicaux) s’appuyant sur l'usage de ces fonctions par division d'un arc d'ellipse. Pour la petite histoire, il fut le beau-père d'Émile Picard.
|
Travaux sur la transcendance des nombres : |
En 1873, dans un mémoire intitulé Sur la fonction exponentielle, Hermite, rendant hommage à Lambert et à Liouville, prouva par un usage subtil des fractions continues et du calcul intégral, la transcendance du nombre e (base des logarithmes népériens) en montrant l'impossibilité d'obtenir une relation de la forme :
N + eaN1 + ebN2 + ... + ehNn = 0
à moins que tous les Ni soient nuls ( a, b, ..., h et N, N1, ..., Nn sont des entiers). En d'autres termes, le nombre e n'est pas algébrique : il ne peut être solution d'une équation polynomiale à coefficients entiers. Le résultat d'Hermite est le premier exemple de nombre transcendant découvert en analyse. On pourra consulter deux extraits du mémoire de Charles Hermite ici et là et le mémoire complet sur le site Gallica de la BnF (» réf.3).
On retiendra ce résultat d'Hermite et Lindemann :
Si a est un nombre réel algébrique non nul, alors ea est transcendant
En savoir plus sur les nombres algébriques : »
L'existence de nombres transcendants fut "découverte" par Liouville par une subtile construction arithmétique de séries numériques. Il faudra attendre le 20e siècle pour apprendre que les logarithmes sont des nombres transcendants. La transcendance de π sera prouvée par Lindemann une décennie plus tard (1882).
» Euler
, Baker
Calcul
élémentaire de e :
»
Calcul de
100 (ou plus) décimales de e :
»
| Théorie des formes quadratiques : |
Généralisant les travaux de Sylvester
et de Cayley
sur les formes algébriques, Hermite précise les
méthodes de réduction des formes
quadratiques (initiées par Gauss), lorsque le corps de scalaires
est C : forme quadratique
hermitienne,
espace vectoriel
hermitien
et généralise ses résultats à un nombre quelconque de variables ainsi qu'à des
formes non nécessairement positives.
| Matrice orthogonale, transposée, conjuguée, adjointe (transconjuguée), hermitienne, symétrique : |
♦ On doit à Hermite la notion de matrice orthogonale : il s'agit d'une matrice carrée M à termes réels ou complexes dont les vecteurs colonnes ci constituent une base orthonormée : les ci sont orthogonaux et unitaires.
Une matrice de rotation plane est orthogonale :
Les matrices de Lorentz dans l'espace-temps à 4 dimensions de Minkowski sont orthogonales.
♦ La matrice transposée d'une matrice M est la matrice notée tM obtenue en échangeant les rôles des lignes et des colonnes. Dans le cas d'une matrice carrée (aij), cette transformation laisse la diagonale invariante : les termes aii (i = j). La transposition des matrices se rencontre dans l'étude des isométries et les changements de bases orthonormées (matrices de passage orthogonales.
Un exemple élémentaire est donné ci-dessous :
Théorème 1 :
Pour toute matrice carrée M, on a det(M) = det(tM) » déterminant d'une matrice
Preuve : pour se convaincre de ce résultat, on pensera que l'on peut développer le déterminant de M suivant la 1ère ligne ou la 1ère colonne.
Théorème 2 :
Pour toute matrice carrée orthogonale M, on a M -1 = tM
Preuve : notons symboliquement c1, c2, ... cn les colonnes de la matrice orthogonale M et écrivons M = (c1 | c2 | ... | cn). Les ci s'interprètent comme des vecteurs orthonormés. Les lignes de tM sont les colonnes de M. Considérons le produit P = tM × M :
L'élément pij de P placé en i-ème ligne et j-ème colonne s'interprète comme le produit scalaire <ci,cj>. M étant orthogonale, <ci,cj> égale 0 si i ≠ j, 1 sinon : par suite P n'est autre que la matrice unité, ce qui montre que M-1 = matrice transposée de M.
Théorème 3 (corollaire) :
Pour toute matrice carrée orthogonale M, on a det (M) = ± 1
Preuve : On note I la matrice unité. Son déterminant est 1. det(M)2 = det(M) × det(tM) = det(M) × det(M-1) = det (M × M-1) = det(I) = 1; donc det(M) = ±1.
Notions de calcul matriciel : » Matrices & changement base : »
♦ La matrice conjuguée d'une matrice M à termes complexes (éléments de C) est la matrice notée M, constituée des éléments conjugués de M.
♦ La matrice adjointe d'une matrice M est la matrice généralement notée M*, égale à la transposée de sa conjuguée :
M* = t M
De cette définition résulte l'appellation synonyme parfois utilisée de matrice transconjuguée. On a manifestement :
♦ Une matrice est dite hermitienne si elle coïncide avec son adjointe :
➔ Dans le cas d'une matrice à coefficients réels ces égalités se réduisent à M = tM; on dit d'une telle matrice qu'elle est symétrique.
Un important théorème de Charles Hermite :
Les valeurs propres d'une matrice coïncidant avec son adjointe (matrice hermitienne M = t M) sont réelles.
Valeurs propres d'une matrice : » Produit scalaire dans C, formes sesquilinéaires et hermitiennes : »
| Polynômes de Hermite : |
Il s'agit, à l'instar des polynômes de Tchebychev ou de Legendre, d'un système de polynômes Hn de degré n, orthogonaux pour le produit scalaire :
En savoir un peu plus : »
| Formule d'Hermite pour l'intégration approchée : |
Soit f une fonction continue sur l'intervalle [-1,1], alors :
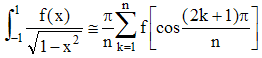
On remarquera, dans cette écriture, que les images de f aux points :
sont les zéros du polynôme de Tchebychev de degré n (k = 0, 1, ..., n-1).
| Les fonctions continues dérivables en aucun point : |
Weierstrass exhiba en 1872 une fonction continue partout mais dérivable nulle part... Hermite se serait horrifié en déclarant :
Je me détourne avec effroi et horreur de cette plaie lamentable des fonctions continues qui n'ont pas de dérivée...
La fonction de Weierstrass : » La fonction de Darboux : »
➔ Pour en savoir plus :
Lissajous