ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 SYLVESTER James Joseph,
anglais, 1814-1897 |
Sources éléments biographiques : CDSB & Applied Probabilty Trust, 1997 (Centenaire de la mort de J. J.Sylvester).
Sylvester étudia les sciences à l'université de Londres (qui deviendra l'University College en 1826), à Liverpool et au Saint-John's College de Cambridge. Sorti second en 1838, il obtint un poste de professeur de physique à l'University College de Londres alors qu'il convoitait un enseignement des mathématiques.
Là, il rencontre De Morgan, un de ses anciens professeurs à Londres, qui l'encourage à poursuivre ses études de mathématiques : il obtient son magister au Trinity College de Dublin (Irlande) en 1841. Entre temps, il avait publié des articles en théorie des nombres et tout particulièrement (1838) un théorème, extension du célèbre théorème de Wilson, qui lui valut, avec l'appui de De Morgan, son élection à la Royal society l'année suivante.
Soit N un entier et p1, p2, ..., pk
tous les entiers inférieurs à N et premiers avec lui, alors le produit p1
× p2 × ... × pk +1
ou, sinon, p1 × p2 × ... × pk - 1 est un
multiple de N
∗∗∗
Vérifier que p1 × p2 × ... × pk
+1 et p1 × p2 × ... × pk - 1 multiples de
N ne peut avoir lieu qu'en dehors de cas triviaux.
Trinity College de Dublin (Irlande)
Sylvester part alors enseigner les mathématiques aux États-Unis où il fait, à l'université de Virginie, un court et désastreux séjour dû à une altercation avec un de ses étudiants et son caractère tempétueux. Rentré en Angleterre trois mois plus tard, il entame des études de droit et trouve un emploi d'actuaire dans une compagnie d'assurances (en charge de l'aspect mathématique et statistique des tarifs et rentabilités). Il rencontre Cayley avec lequel il se lie d'amitié, et qui se voue lui aussi au métier d'avocat tout en publiant des articles mathématiques !
Avocat, mathématicien et musicologue averti, ce n'est qu'en 1855 qu'il obtint une chaire de mathématiques à l'Académie royale militaire de Woolwich (1855-1870). De retour aux États-Unis, Sylvester enseigna à la Johns Hopkins University de Baltimore de 1876 à 1883 et terminera sa brillante carrière à Oxford (jusqu'en 1894).
Élu à l'Académie des sciences de Paris en 1863, James Sylvester présida la London Mathematical society (1866), fut le fondateur de l'American journal of mathematics (1878) et reçut la médaille De Morgan (1887) ainsi que la médaille Copley de la Royal society en 1880, une distinction en principe octroyé aux physiciens et biologistes.
Médaille Sylvester :
Trois ans après sa mort, en 1901, une médaille de la Royal Society est instaurée en l'honneur de Sylvester. Depuis 2009, son objectif est de récompenser et encourager de jeunes mathématiciens la recherche mathématique :
En savoir un peu plus sur la médaille Sylvester : »
| La théorie des déterminants : |
Les travaux de Sylvester portèrent principalement, en collaboration avec Cayley, sur la théorie des déterminants fondée sur l'étude des équations polynomiales, les formes algébriques et leurs invariants (formes quadratiques et leurs réductions en particulier).
Les formes multilinéaires et la théorie des déterminants : »
Le terme de déterminant, au sens de permettant d'amener à la conclusion n'est pas nouveau : adopté par Cauchy, il avait été utilisé auparavant par Gauss, sans plus de développement, dans ses Disquisitiones Arithmeticae (1801) pour désigner les nombres comme b2 - ac intervenant dans la réduction des formes quadratiques du type ax2 + 2bxy + cy2 en tant que déterminant de la matrice symétrique associée.
➔ Selon Florian Cajori, Sylvester est à l'origine de l'usage Δ = b2 - 4ac (Δ = Delta = d majuscule grec) dans le calcul des solutions de l'équation générale du second degré de la forme ax2 + bx + c = 0 ou bien Δ = b2 - ac (discriminant réduit), dans le cas de l'équation ax2 + 2bx + c = 0.
La notation actuelle des déterminants, entre deux barres, comme ci-dessous, est due à Cayley :
Cauchy utilisa en 1840 une notation proche. L'usage des déterminants tant en algèbre qu'en géométrie a montré tout l'intérêt de tableaux numériques et l'avantage d'une notation simplifiée des systèmes d'équations. De là, on peut bâtir un nouveau concept et de nouvelles opérations : la théorie des matrices qui sera l'œuvre maîtresse de Cayley.
Outre l'arithmétique, Sylvester intervint également dans la théorie (naissante) des graphes : on lui doit le terme de graphe (vers 1880), ainsi que celui de matrice (1850).
| Un cas élémentaire de notation matricielle et de son usage : |
Le système linéaire défini par les équations :
|
3x - 4y = 7 |
peut s'écrire matriciellement :
.
Le tableau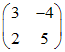 
est une matrice carrée (autant de lignes que de colonnes)
d'ordre 2. Son déterminant est 15 + 8 = 23
≠ 0, elle est donc
inversible : il existe une unique solution. Par inversion de cette matrice, on a
:
La solution du système est donc donnée par x = 1, y = -1.
» Matrice inverse , Méthode du pivot
Wantzel