ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 RIEMANN Bernhard,
allemand, 1826-1866» L'intégrale de Riemann | fonction ζ zêta et nombres premiers | Hypothèse de Riemann | Géométrie différentielle |
Fils de pasteur, voué
de par la volonté paternelle à des études théologiques, le jeune Bernhard entre
à l'université de Göttingen (1846) afin
étudier la philosophie malgré son attrait et ses brillantes capacités pour les
mathématiques. Sa rencontre avec Gauss,
mathématicien et astronome réputé, sera déterminante : il sera mathématicien.
Gauss, alors âgé de 74 ans, dirigea sa thèse (1851) sur les fonctions d'une variable complexe en la célèbre université de Göttingen. Riemann fut lui-même professeur à Göttingen, succédant à ce dernier en 1859 (Dirichlet avait lui-même succédé à Gauss quatre ans plus tôt). Hélas, cet illustre mathématicien mourut prématurément à peine âgé de 40 ans, atteint de tuberculose à Selesca (lac Majeur, Italie) où il se soignait.
C'est dans sa thèse de 1851 (Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen complexen Größe = Fondements pour une théorie générale des fonctions d'une variable complexe), qu'apparaît la notion de surface de Riemann permettant de donner un sens à une fonction complexe susceptible de prendre plusieurs valeurs : les fonctions multiformes. Une vision totalement nouvelle, voire révolutionnaire, d'une théorie précédemment élaborée par Cauchy qui y consacra 30 ans de sa vie.
Avec sa théorie des surfaces (Sur les hypothèses qui servent de fondement à la géométrie, 1854), généralisée abstraitement à n dimensions : les Variétés (Mannigfaltigkeit), on pénètre dans des géométries non euclidiennes avec la généralisation de la notion de distance, qui seront, 50 ans plus tard, pour Einstein et Minkowski les outils indispensables pour la mise en place de la théorie de la relativité.
Notion de variété & géométrie différentielle : »
Dans ces nouveaux espaces, avec la recherche de propriétés invariantes par "transitions" continues, Riemann apparaît comme un des pères de la topologie moderne, branche extrêmement féconde et toujours actuelle des mathématiques entrevue par Euler et Leibniz et que ce dernier nomma Analysis situs, terme utilisé jusqu'au 20è siècle, avec Poincaré, par exemple.
Notions de topologie : »
En analyse, Riemann développa la théorie des fonctions abéliennes et des fonctions elliptiques et compléta les travaux de Dirichlet, son maître, sur les séries trigonométriques et leurs problèmes de convergence. Dans ce dernier contexte, son nom reste attaché à sa célèbre formalisation de l'intégrale :
| Intégrale de Riemann, primitive d'une fonction : |
Non satisfait de la théorie de l'intégration de
Cauchy portant sur les fonctions continues qui lui paraît insuffisante pour manipuler certaines séries de Fourier (de fonctions "peu" régulières), Riemann publie (1854) une rigoureuse théorie de l'intégration pour les fonctions bornées sur un intervalle fermé.On sait depuis Mercator et Leibniz, que si une fonction est positive, l'intégrale sur un intervalle [a,b] :
(notation due à Fourier) évalue l'aire du domaine « sous la courbe », parfois appelée hypographe (» convexité). L'intégrale est obtenue en encadrant la fonction f entre deux suites de fonctions en escalier : on parle de quadrature, calcul d'aire basé sur la décomposition en rectangles (ou carrés au sens étymologique) de la surface à évaluer.
Étude de l'intégrale au sens de Riemann, calcul
approché
: »
On apprend en classe Terminale que si la fonction f est continue sur [a,b], il existe au moins une fonction F dérivable sur [a,b] telle que F'(x) = f(x). Une telle fonction F est appelée primitive de f sur [a,b].
Toute autre primitive G de f ne diffère de F que par une constante
En effet si G' = F', alors G' - F' = (G - F)' est la fonction nulle; donc G - F est une fonction constante :
G'(x) = f(x) ⇒ ∃ k∈R, G(x) = F(x) + k
On a le résultat fondamental :
♦ Une
primitive d'une fonction continue peut ne pas être calculable ! Si vous
choisissez une fonction au hasard, la probabilité que vous en calculiez une
primitive est très faible... Deux exemples : x → cos
x2
, x → 1/lnx
: »
logarithme intégral. Ce qui n'empêche pas d'en calculer des intégrales au moyen
de méthodes d'intégration approchée ou de
développement en série.
∗∗∗
Lagrange
et la notion de primitive, exercices ,
calcul de quelques intégrales (niveau SUP)
♦ Dans le cas d'une fonction x → F(x) définie sur un intervalle J par une intégrale où x apparaît dans au moins une borne d'intégration, comme ci-dessous où h est une fonction de x, on parle de fonction définie par une intégrale :
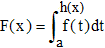
Si φ est une primitive de f et si h est dérivable sur J, on a F(x) = φ(h(x)) - φ(a). Le théorème de dérivation des fonctions composées conduit alors à :
F'(x) = φ'(h(x))×h'(x) = f(h(x))×h'(x)
Si la borne a d'intégration dépend également de x, on lui applique le même procédé :
Considérons pour x > 0 , F(x) =∫[1/x,2x]
dt/t
= ln(2x) - ln(1/x)
= 2lnx +
ln2. Si
nous dérivons, on obtient F'(x)
= 2/x. Utilisons maintenant le résultat énoncé : F'(x)
= 1/2x×2 - x×(-1/x2) = 1/x + 1/x = 2/x.
Cas d'une fonction de deux variables définie par une intégrale : » Valeur principale de Cauchy : »
| Intégrale de Riemann-Liouville : |
| La géométrie différentielle : |
Dans son magistral traité de 1854, Les hypothèses qui servent de fondement à la géométrie, suite aux travaux de Gauss dans l'étude des surfaces, Riemann développa ce qui deviendra une branche maîtresse des mathématiques : la géométrie différentielle.
L'objectif fut de généraliser les propriétés métriques et différentielles des surfaces "usuelles" de l'espace euclidien à des espaces "courbés" considérés comme espaces de référence et non plus comme plongés dans un espace plus vaste de dimension supérieure : on parle de variétés.
Une courbe plane ou gauche (dans l'espace 3D) est une variété de
dimension 1 :
» Courbe gauches
La sphère, surface d'une boule, est une variété de dimension 2.
Une variété est dite algébrique si elle admet une équation polynomiale du type f(x,y,z,...) = 0.
Une conique, un cercle sont des variétés algébriques de dimension 1, la sphère est une variété algébrique de dimension 2 (surface).
En hommage à Riemann, on appelle variété riemannienne, une variété sur laquelle on peut définir une métrique (distance cohérente entre deux points de la variété). Une telle variété abstraite (elle n'est plus considérée comme partie d'un espace plus vaste) peut alors être munie d'une topologie (variété topologique). On peut y définir des coordonnées, une orientation, un produit scalaire (de vecteurs tangents), des transformations et des propriétés différentielles (variété différentielle). On entre alors dans le monde de la géométrie différentielle et de la topologie différentielle.
➔ Les pays anglo-saxons utilisent algebraic variety pour désigner une variété algébrique et manifold, adjectif substantivé signifiant varié pour désigner une variété topologique.
Variétés & notions fondamentales de la géométrie différentielle : »
Le
paraboloïde hyperbolique, en forme de selle de cheval, est une variété de
dimension 2
| Fonctions multiformes, surfaces de Riemann : |
Dans sa thèse de 1851, prolongeant les travaux de Cauchy sur les fonctions d'une variable complexe et afin de donner un sens aux fonctions multiformes à valeurs complexes (un point peut posséder plusieurs images), Riemann conçoit la notion appelée de nos jours surface de Riemann et plus généralement de variété riemannienne.
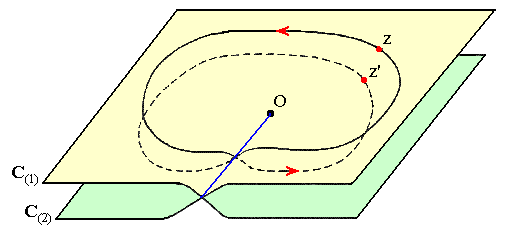
Sur une telle "surface", constituée de "feuillets" raccordés continûment, une fonction multiforme devient uniforme (un point n'a qu'une seule image).
En savoir plus sur ces fonctions et
ces surfaces :
»
»
Intégrale complexe ,
théorème des résidus ,
Théorème de Riemann-Roch
| Riemann et les géométries non euclidiennes : |
Ces travaux en géométrie différentielle conduisent ainsi Riemann à s'intéresser vers la fin des années 1850 (édition posthume, 1867) au célèbre 5ème et controversé postulat d'Euclide (souvent appelé postulat des parallèles) et à décrire une géométrie non euclidienne en remplaçant ledit postulat par l'impossibilité de mener par un point une parallèle à une droite donnée !
On n'aboutit ainsi à aucune contradiction et une concrétisation de cette géométrie est celle de la sphère, surface à courbure constante positive, où les "droites" (géodésiques : trajectoires de cheminement minimum entre deux points) sont les grands cercles : ceux dont le centre est celui de la sphère. On parle de géométrie elliptique, s'opposant à la géométrie hyperbolique de Lobatchevski.
Ci-contre, étant donnés deux points S et S' diamétralement opposés sur la sphère, les "droites" rouge et bleu sont perpendiculaires à la "droite" équatoriale noire. Dans cette géométrie, on pourrait alors les considérer comme "parallèles", mais se coupant en S et S'...
Notions sur les géométries non euclidiennes : » Géodésique, loxodromie, orthodromie : »
| Fonction ζ (zêta), séries de Riemann, théorème des nombres premiers : |
Guidée par une géniale intuition, Riemann prolonge au plan complexe la fonction s → 1/ns
, déjà étudiée par Euler dans le cas réel, dans le but de résoudre le difficile problème de la distribution des nombres premiers, au sujet duquel Gauss, son ancien professeur, avait planché durant toute sa carrière en conjecturant avec Legendre :
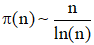(pour n tendant vers l'infini)
π(n) désignant le nombre de nombres premiers inférieurs à n (notation de Legendre).
En 1859, il publie un mémoire fondamental intitulé Über die Anzahl der Primzahlen unter einer gegebenen Größe (Sur les nombres premiers inférieurs à une grandeur donnée, » réf.10). En notant traditionnellement s = σ + it (σ et t sont respectivement les parties réelle et imaginaire de s), les séries de terme général 1/ns, aujourd'hui appelées séries de Riemann, sont absolument convergentes lorsque σ > 1 et divergent sinon.
Pour σ > 1, les sommes de ces séries définissent donc des nombres complexes que Riemann note au moyen de la lettre grecque ζ (prononcer zêta), ce qui conduit à une notation fonctionnelle s → ζ(s) :
Étude de la convergence : » » Séries (généralités, convergence)
Si s est un entier naturel pair (non nul), les nombres ζ(s) sont irrationnels et transcendants, comme :
car il est prouvé que pour n ≥ 1 :
où les b2n sont les nombres de Bernoulli.
Ces nombres sont aussi liés :
aux nombres
de Bernoulli
Bn par la formule :
ζ(2n)
= 1 + 1/22n + 1/32n + 1/42n + ... =
22n-1 × π2n × B2n/(2n)!
à la
constante d'Euler par la belle formule :
C = 1/2 × ζ(2)
- 1/3 × ζ(3)
+ 1/4 × ζ(4)
- ... + (-1)n/n × ζ(n)
➔ Lorsque s est impair, s = 2n + 1, n ≥ 2, la nature irrationnelle ou transcendante de ζ(2n + 1) n'est pas connue : elle reste un problème ouvert. Le cas ζ(3) fut partiellement résolu par le français Roger Apery par le biais de son analyse non standard : ce nombre est irrationnel mais on ne sait pas s'il est transcendant.
Quelques valeurs de ζ(n), n impair (
source OEIS, A013663, A013665, ...A013671) :i Un résultat inattendu où l'analyse transcendante s'immisce dans l'arithmétique a priori "élémentaire" :
La probabilité pour que n nombres entiers choisis au hasard soient premiers entre eux est 1/ζ(n)
Ainsi, la probabilité que deux entiers non nuls choisis au hasard soient premiers entre eux est 6/π2, soit environ 0,61. Ce résultat fut obtenu par Cesaro.
Une preuve fausse (à titre didactique) et deux preuves justes... : »
♦ Nombres premiers et fonction logarithme intégral :
Riemann a prouvé
(» réf.6, 10, 11e) que les zéros réels autres que 0 de la fonction ζ sont les entiers négatifs pairs : du type - 2, - 4, ..., -2n, ... On les qualifie aujourd'hui de triviaux ! Par des considérations relativement simples, Euler avait montré dans le cas s réel l'identité qui porte aujourd'hui son nom :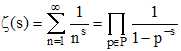
(e1)ce qui peut s'écrire :
où P désigne l'ensemble infini des nombres premiers : P = {2, 3, 5, 7, 11, ...} : ce qui montre encore que la fonction ζ est liée aux nombres premiers et à leur répartition (distribution) dans l'ensemble N des entiers naturels. Et on a ce beau résultat :
La conjecture de Gauss-Legendre π(n) ~ n/ln(n) est
équivalente à l'absence de zéros de la fonction ζ sur la droite
σ = 1
du plan complexe :
ζ(1 + it) ≠ 0 pour tout t réel
♦ Équation fonctionnelle de Riemann (lien entre ζ et Γ) :
L'identité d'Euler ci-dessus permet de montrer que pour toute valeur de s = σ + it dans le demi-plan de convergence σ = Re(s) > 1, il n'existe aucun zéro. L'incertitude se présente dans la bande 0 < σ < 1 du champ complexe où Riemann prouva que l'on peut prolonger analytiquement la fonctions ζ en une fonction holomorphe pour tout s ≠ 1. Le point s = 1 est un pôle simple de résidu 1.
(» réf.6, Ch.II, réf.11d,11e). Au moyen de la fonction Γ de Euler, on obtient cette belle formule :
(e2)
sin désigne ici le développement en série (prolongement analytique dans C) de la fonction trigonométrique sinus usuelle.
➔ On voit que le changement de s en 1 - s laisse la formule invariante, ce qui fait présager du rôle crucial de s = 1/2 (symétrie par rapport à la droite s = 1/2 du plan complexe. Lorsque s = 1/2, on a Γ(1 - s) = Γ(1/2) = √π ≠ 0 et ζ(s) = ζ(1 - s) = ζ(1/2). En supposant ζ(1/2) ≠ 0, on aura, selon (e2), sin(π/4) = 0; par suite ζ s'annule en s = 1/2 : » hypothèse de Riemann
Faisant usage du logarithme intégral (li), introduit par Gauss, et par des transformations d'une grande subtilité, Riemann conjecture que le nombre π(x) de nombres premiers inférieurs à l'entier x ≥ 2, autre qu'une puissance d'un nombre premier, vérifie :
1.
2. 
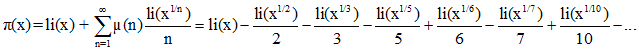
µ(n) désignent les
nombres de Möbius.
3. π(x) = li(x) + O(x × ln
Il faudra attendre une quarantaine d'années pour que ces puissantes conjectures soit complètement prouvées. La première sera le fruit du travail de Carl von Mangoldt en 1895, trente ans après la mort de Riemann. L'année suivante, après les avancées significatives de Tchebychev en 1852, ce sera le fait, indépendamment, du français Hadamard et du belge de La Vallée-Poussin. La conjecture devient le théorème des nombres premiers : π(x) ~ x/ln(x) pour x tendant vers l'infini. Autrement dit :
En savoir plus sur la distribution des nombres premiers : »
i Hans Carl Friedrich von Mangodt (1854-1925), mathématicien allemand, spécialiste en théorie des nombres. Il fut un étudiant de Kummer qui dirigea sa thèse sur la représentation d'équations algébriques par des séries à l'université de Berlin en 1878. » Bombieri
♦ Hypothèse de Riemann :
C'est dans son mémoire de 1859 que Riemann énonce sa célèbre conjecture (hypothèse) :
Lorsque la partie réelle de s est comprise entre 0 et 1, les zéros de ζ(s) ont tous 1/2 pour partie réelle.
(» réf.14). En 1914, Hardy prouva l'existence d'une infinité de tels zéros et une centaine de milliards de zéros non triviaux ont aujourd'hui été découverts : tous sur la droite σ = 1/2. Ce qui ne prouve rien quant à la véracité de la conjecture qui perdure depuis 160 ans. On pourra lire un intéressant historique des recherches numériques des zéros en consultant la page Wikipédia consacrée à ce sujet (» réf.13).➔ L'hypothèse de Riemann fit l'objet du 8ème problème de Hilbert énoncé en 1900. Elle résiste depuis 160 ans. Aucun contre-exemple, aucune preuve convaincante. En 1903, le mathématicien Danois Jörgen Gram prouva que les 15 premiers zéros sont bien d'abscisse 1/2
Weil consacra une importante part de ces travaux à l'étude de l'hypothèse de Riemann et émit lui-même plusieurs conjectures que Deligne prouvera (1973) sans pour autant solutionner complètement ce très difficile problème. Rappelons ici cette belle et modeste pensée de l'immense mathématicien que fut André Weil relative à l'hypothèse de Riemann :
Quand j'étais jeune, j'espérais la démontrer. Quand je suis devenu un peu plus vieux, j'ai encore eu l'espoir de pouvoir lire et comprendre une démonstration de l'hypothèse de Riemann. Maintenant, je me contenterais bien d'apprendre qu'il en existe une démonstration.
Le 8 juin 2004, un mathématicien français installé aux USA, Louis de Branges de Bourcia (1932-, université de Perdue, Indiana, USA) affirme avoir prouvé la célèbre hypothèse mais le raisonnement était malheureusement erroné. Ce même mathématicien avait prouvé (1985) la conjecture de Bieberbach énoncée en 1916.
➔ Il est prouvé
(» réf.6, par exemple) que si l'on suppose validée l'hypothèse de Riemann, le théorème des nombres premiers s'exprimerait alors par :π(x) = li(x) + O(√x × lnx) au lieu de π(x) = li(x) + O(x × lnx) »
notation de LandauC'est dire que le terme d'erreur de l'approximation de π(x) par li(x) est grandement diminué.
La preuve de l'hypothèse de Riemann a été mise à prix en mai 2000 par le Clay Mathematics Institute : un million de $US. Elle reste improuvée encore aujourd'hui (janvier 2014) et certains mathématiciens, comme Henri Berliocchi, osent se risquer à la contester.
♦ Hypothèse de Riemann généralisée (dite HRG) :
En simplifiant à l'extrême, cette hypothèse relative aux progressions arithmétiques d'entiers premiers, fait appel aux séries L, généralisant celle de Riemann, que Dirichlet introduisit dans ses travaux sur le sujet un demi-siècle au préalable :
Si la fonction L(z,χ) admet un zéro dans la bande "critique" 0 < Re(z) < 1, alors Re(z) = 1/2.
i Selon la source Wikipedia (fr & en), cette hypothèse aurait été conjecturée par le mathématicien allemand Adolph Piltz (1855-1940) dans sa seconde thèse de 1884. Il fut étudiant à Berlin auprès de Kummer qui dirigea sa première thèse (1881). Ses recherches portent exclusivement sur la théorie analytique des nombres. La thèse de Piltz est en ligne (» réf.18) mais le texte allemand est très difficile à déchiffrer...
| Équation de Riemann : |
Il s'agit d'une équation différentielle linéaire du second ordre, rencontrée en physique mathématique, ayant trois points singuliers a, b et c, de type Fuchs :
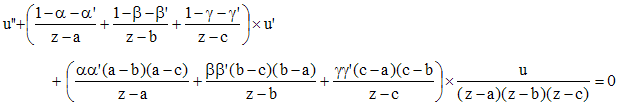
Un cas particulier de cette équation est fourni par l'équation hypergéométrique de Gauss et l'équation de Kummer.
➔ Pour en savoir plus :
Cremona
Luigi
» 
»
