
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Programmation de la méthode élémentaire des rectangles , Autres méthodes , Intégration par parties L'intégrale selon Cauchy , L'intégrale selon Lebesgue |
On sait depuis Mercator et Leibniz, que si f est une fonction positive et supposée continue sur un intervalle [a,b], l'intégrale de f sur cet intervalle évalue l'aire sous sa courbe représentative dans un repère du plan.
S'inspirant de l'intégrale de Cauchy, basée sur cette même conception géométrique mise en place en 1821-1823 pour les fonctions continues, Riemann élargit le concept d'intégrale à des fonctions numériques non nécessairement continues mais bornées sur l'intervalle d'étude [a,b] et partout définies sur [a,b] sauf éventuellement en un nombre fini ou dénombrable de points isolés.
Les fonctions en escalier :
Étant donné un intervalle [a,b] de R, on appelle subdivision de cet intervalle une suite finie (xi) de points de [a,b] :
a = xo < x1< x2 < ... < xi < ... < xn= b
L'intervalle [a,b] est ainsi partagé en n sous-intervalles disjoints ]xi,xi+1[ dont il est la réunion.
On appelle pas de la subdivision le plus grand des écarts xi+1- xi.
La subdivision est dite régulière si les xi sont régulièrement espacés. C'est dire que les xi sont en progression arithmétique de raison (b - a)/n.
Une fonction numérique f est dite en escalier (on dit aussi constante par morceaux) pour signifier qu'il existe un intervalle [a,b] et une subdivision (xi) de cet intervalle tels que :
f est nulle en dehors de [a,b];
f ne prend que des valeurs finies;
f est constante sur chaque ]xi,xi+1[;
Intégrale d'une fonction en escalier :
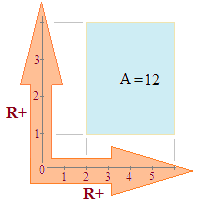
➔ L'intégrale d'un pavé A de R2 rapporté à repère orthogonal quelconque est une mesure de son aire, indépendamment de toute unité choisie sur les axes. Par définition, un pavé dont les côtés sont parallèles aux axes aura pour aire le produit Δx × Δy des deltas de ses cotes en x et y. Dans l'illustration ci-dessous, l'aire de A est (6 - 2)(4 - 1) = 12. C'est à dire 12 unités d'aires (» quadrature).
Soit φ en escalier sur [a,b]. Si yi est la valeur (éventuellement négative) de φ sur Ai = ]xi,xi+1[, on remarque que :
φ = y1 × 1A1 + yi × 1A2 + ...+ yn × 1An
φ
est ainsi combinaison linéaire des fonctions
caractéristiques 1Ai
des sous intervalles ]xi,xi+1[.
Rappelons que
1Ai
(x) = 1 si x
∈Ai , 0
sinon (»
Dirichlet).
L'intégrale de φ sur [a,b] est alors :

Exemple :
à droite, la subdivision de [a,b] = [1,11] est régulière, de pas
2.
L'intégrale de φ sur [a,b] est 3 + 5 - 2 -1 +2 = 7.
Intégrale d'une fonction bornée :
Soit maintenant f une fonction numérique bornée sur [a,b]. Parmi toutes les fonctions en escalier sur [a,b], il y a celles qui majorent f : fonctions g telles que f(x) ≤ g(x) pour tout x de [a,b], et celles qui minorent f : fonctions h telles que h(x) ≤ f(x).
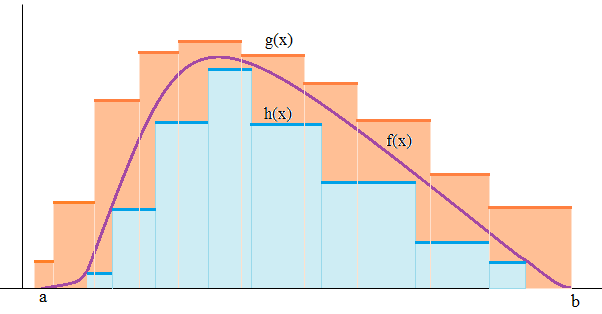
Dans cette illustration, la positivité de f n'est supposée
que pour une meilleure compréhension
Notons respectivement I(g) et I(h) les intégrales de g et h. La fonction f étant bornée, I(g) admet une borne inférieure inf_I(g) et I(h) une borne supérieure sup_I(h). Par définition, f est dite intégrable au sens de Riemann sur [a,b] lorsque inf_I(g) = sup_I(h) et son intégrale est le nombre :

» Ce principe d'encadrement n'est pas sans rappeler la subtile approche de la circonférence (périmètre du cercle) par Archimède, appelée aujourd'hui méthode des périmètres, consistant à encadrer le cercle entre deux suites de polygones réguliers par défaut et pas excès.
Théorème (ou critère) de Riemann :
Le résultat précédent, n'est pas vraiment opérationnel, raison pour laquelle, Riemann prouve un résultat à rapprocher de celui de Cauchy : considérons un intervalle [a,b] sur lequel une fonction f est bornée et soit une subdivision (xi) de [a,b] :
Sur chaque [xi, xi+1], on remplace l'arc de courbe représentatif de f par un segment d'ordonnée f(ci) avec xi < ci < xi+1 : c'est dire que f est remplacé par une fonction en escalier. La somme :
sur cet intervalle, est une somme de Riemann attachée à f sur l'intervalle [a,b] (appellation due à Darboux).

Riemann montre alors que :
Si, lorsque n tend vers l'infini, de sorte que le plus grand des pas xi - xi-1 tende vers 0, la somme Sn admet une limite finie indépendamment du choix de la subdivision et qui n'est autre que l'intégrale de f sur [a,b] (au sens de Riemann) :

Toute fonction numérique continue sur [a,b] est intégrable au sens de Riemann sur cet intervalle.
Une fonction numérique bornée sur [a,b] est intégrable au sens de Riemann sur cet intervalle si et seulement si ses sommes de Riemann sont convergentes.
Toute fonction à variation bornée sur [a,b], en particulier les fonctions monotones (c'est à dire croissantes ou décroissantes) sont intégrables au sens de Riemann.
Toute fonction admettant une limite finie à gauche et à droite en tout point de [a,b], est intégrable au sens de Riemann.
Théorème fondamental :
Si F est une primitive de f sur un intervalle J contenant [a,b], c'est à dire une fonction F dérivable sur [a,b], telle que F'(x) = f(x), alors :

➔ Mais le calcul d'une primitive n'est pas toujours évident, même pour une fonction d'apparence simple comme par exemple x → cos(x2). On peut avoir recours à un développement en série de la fonction. Pour ce cas, on devrait alors écrire :
cos x = 1 - x2/2! + x4/4! - x6/6! + ..., puis cos(x2) = 1 - x4/2! + x8/4! - x12/6! + ...
D'où une complication (la recherche du développement n'est pas
non plus toujours évidente) et un souci pour la précision du calcul. Les
mathématiciens se sont alors penchés sur des méthodes d'approximation :
Quelques propriétés élémentaires mais fondamentales :
La notation I(f), ou plus précisément I[a,b](f), signifiera ci-dessous l'intégrale de f sur [a,b]
∗∗∗
1.
niveau TerS :
Aire sous la parabole
2.
niveau SUP :
Intégrale de Wallis
3.
niveau SUP :
Calcul d'intégrales & primitives diverses
4.
Autres exercices :
niveau bac ,
niveau sup.
➔ Pour en savoir plus :