
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Équation aux dérivées partielles | Condition d'extrémum d'une fonction de deux variables | Équations différentielles ordinaires |
La notion de dérivée partielle est fondamentale en analyse, en géométrie différentielle et dans toutes les branches de la physique où on la rencontre systématiquement.
Si f est une fonction numérique de plusieurs variables, la fonction dérivée partielle de f par rapport à l'une d'elles s'obtient en dérivant l'expression de f par rapport à cette dernière et en considérant les autres comme des constantes.
➔ On voit déjà ici le distinguo entre dérivation ordinaire (fonction d'une seule variable) et dérivation partielle (fonction de plusieurs variables) qui conduit à parler d'équation différentielle ordinaire (EDO) dans le cas d'une seule variable.
Par exemple si f est fonction de deux
variables u et v, la
dérivée partielle de f par rapport à u
est notée
![]() , notation de
Legendre calquée sur celle
qu'utilisa
Leibniz, à savoir df/du dans le
cas d'une seule variable (»
notation ∂). La
dérivée partielle par rapport à u, s'obtient en dérivant f par rapport à u en considérant v comme une
constante. Pour simplifier, on utilise parfois
fu'.
, notation de
Legendre calquée sur celle
qu'utilisa
Leibniz, à savoir df/du dans le
cas d'une seule variable (»
notation ∂). La
dérivée partielle par rapport à u, s'obtient en dérivant f par rapport à u en considérant v comme une
constante. Pour simplifier, on utilise parfois
fu'.
Comme dans le cas d'une variable, la fonction dérivée partielle de f par rapport à une de ses variables s'obtient par la limite du taux d'accroissement :

Différentielle d'une fonction de plusieurs variables : »
Dérivée partielle seconde :
L'usage des dérivées partielles secondes est très fréquent tant en analyse mathématique qu'en sciences physiques :
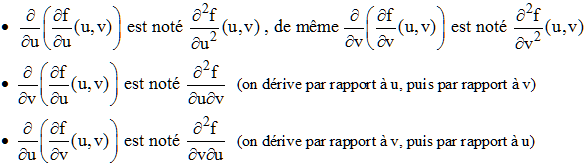
Les deux dernières dérivées partielles sont dites mixtes. On démontre que si les dérivées partielles mixtes existent et sont continues, alors elles sont égales : l'ordre de dérivation est indifférent : c'est un résultat établi dans toute sa généralité par Karl H. Schwarz :
| Théorème de Schwarz : |
Soit f est une fonction numérique de deux variables x et y. Si f est de classe C2 (admettant des dérivées partielles continues d'ordre 1 et 2 par rapport à chaque variable), alors :
![]()
| Condition nécessaire d'extremum d'une fonction de plusieurs variables : |
Soit f une fonction des variables indépendantes u, v, w, ... , dérivable au voisinage d'un point (u
o,vo,wo, ...) :Une condition nécessaire pour que f admette
un extremum en ce point (minimum ou maximum) est que
toutes ses dérivées
partielles soient nulles en ce point.
C'est dire que (uo,vo,wo, ...) est un point critique de f.
Par exemple, pour trois variables u, v et w, on devra donc avoir :

Nature de l'extremum dans le cas de deux variables indépendantes:
Le développement de Taylor d'ordre 2 d'une fonction de plusieurs variables permet de lever l'ambiguïté quant à la nature de l'extremum (» réf1, Ch.XI-7, réf.2, Ch.V-2) lorsque ce développement n'est pas dégénéré. On pousse alors à l'ordre 3 ou plus (» cet exercice).
Soit f une fonction de deux variables u et v de classe C
2 (deux fois continument dérivable) au voisinage d'un point (uo,vo) et admettant en ce point un extremum (annulant donc ses dérivées partielles premières). Posons, en omettant les variables (uo,vo) afin de simplifier les écritures:
Si Δ > 0 : f admettra un minimum (resp. un maximum), suivant que ∂2f/∂u2 (ou ∂2f/∂v2 qui possède alors le même signe) est strictement positive (resp. négative).
Si Δ < 0 : ni maximum, ni minimum.
Si Δ = 0 : cas douteux. » cas d'un point selle
∗∗∗
Applications élémentaires :
Volume maximal ,
Aire minimale à volume donné ,
Étude d'une fonction scalaire (deux
études : minimum et maximum)
Concernant cet important sujet, on consultera la page consacrée à Otto Hesse décrivant une méthode générale pour connaître la nature d'un extremum d'une fonction de plusieurs variables.
Courbure des surfaces : » Indicatrice de Dupin : »
| Équations aux dérivées partielles : |
Une équation aux dérivées partielles est une équation dont l'inconnue, une fonction φ, apparaît au moyen de ses dérivées partielles par rapport à l'une au moins de ses variables x, y, ... et devant généralement vérifier des conditions initiales (valeurs données) ou des conditions aux limites, comme tendre vers 0 pour x infini.
Lorsque l'équation est définie sur un ouvert U (intervalle, disque, boule, ...), la condition peut aussi, par exemple, être φ = 0 sur le bord de U.
On rencontre de telles équations tout particulièrement en géométrie différentielle (fonctions harmoniques par exemple) et, généralement à l'ordre 2 (dérivées partielles secondes) dans toutes les branches de la physique et des sciences de la nature comme :
l'électrostatique, l'électromagnétisme (propagation du potentiel dans un câble en tant que signal électromagnétique, le potentiel électrostatique, la théorie du signal );
la thermodynamique (équation de la chaleur), l'hydrodynamique, la théorie des marées;
la théorie des cordes vibrantes, la propagation du son;
l'aéronautique, l'astrophysique (potentiel gravitationnel, également dit newtonien), la mécanique céleste (dont la théorie de la relativité d'Einstein);
la théorie cinétique des gaz (équation de Boltzmann);
la mécanique des fluides, la météorologie, l'élasticité;
...
Par exemple :
♦ Équation des cordes vibrantes : d'Alembert (1746)
![]()
♦ Équation de la chaleur : Fourier (1812)

♦ Équations de Laplace (1782) :

♦ Équation de Poisson, potentiel de volume de densité ρ (1813) :

♦ Équation de Boltzmann (1872) : »
Villani♦ Équation d'Heaviside (dite des télégraphistes), résolue par Poincaré :

♦ Un exemple rudimentaire :
On suppose connu que : ∂f/∂u = 2u - v avec la condition f(1,0) = 1. La variable v doit ici être regardé comme une constante et par suite f(u,v) = u2 - uv + k. Mais cette constante k d'intégration peut dépendre de v et nous devons écrire plus précisément :
f(u,v) = u2 - uv + k(v) avec 1 = f(1,0) = 1 + k(0)
La solution est alors : f(u,v) = u2 - uv + k(v) avec k(0) = 0. On voit là un manque d'informations sur la fonction k qui peut être de toute nature (polynomiale, logarithmique, exponentielle, trigonométrique, ...). Dans le cas général, autrement plus difficile, un manque d'informations sur les conditions initiales est un problème majeur de ce type d'équations.
Les problèmes posés par la physique orientent également les recherches de Daniel Bernoulli sur le développement des fonctions en série trigonométrique (ou l'existence de solutions sous forme de-) que Euler, et surtout Fourier et Dirichlet, finaliseront.
En 1950, Laurent Schwartz crée une extension
de la notion de fonction avec la théorie des
distributions. Ce nouveau concept, qui lui valut la
médaille Fields, va bouleverser l'analyse
classique et fournir l'outil indispensable à la résolution des équations aux
dérivées partielles linéaires.
Avec la complexité des problèmes rencontrés : systèmes d'équations aux dérivées partielles d'ordre élevé et nombreuses conditions aux limites, sont apparues, tout comme pour les équations différentielles ordinaires, des méthodes de résolution approchée. On parle de discrétisation par différences finies et par éléments finis où l'apparition des ordinateurs, dès les années 1940, apportera des solutions satisfaisantes. Pour certains phénomènes évolutifs, on s'intéresse d'ailleurs plus au comportement dans le temps des solutions (propriétés qualitatives) qu'à leur expression mathématique (propriétés quantitatives), en particulier :
régularité (non nullité simultanée des dérivées partielles en un point);
stabilité (de faibles changements dans les valeurs des paramètres n'induisent pas de fortes variations dans les solutions : pas d'effet papillon, pas de chaos, pas de catastrophes...). La stabilité mécanique du système solaire prouvée par Laplace (1783) est un exemple historique fondamental.
»
Thomentropie : évolution d'un système vers un désordre irrémédiable... La fonte d'un glaçon, la disparition, semble-t-il inéluctable de la banquise aux pôles de notre planète, le vieillissement (tout simplement) sont des cas d'entropie.
Méthode des différences finies : » Notion d'entropie : »
La résolution des équations aux dérivées partielles est généralement très difficile :
La difficulté de résolution apparaît dès le 1er ordre et la recherche de solutions convenables parmi les solutions générales trouvées est un casse-tête du même ordre eu égard au problème étudié et aux conditions aux limites (contraintes aux bornes de l'intervalle d'étude).
Lagrange a cependant prouvé qu'une équation aux dérivées partielles du 1er ordre peut toujours se ramener à la résolution d'une équation différentielle du même ordre.
Dans le cas de deux variables indépendantes x et y, une équation aux dérivées partielles, d'inconnue la fonction numérique z = f(x,y), est dite linéaire du 1er ordre si elle peut se ramener à la forme :
 (e)
(e)
les dérivées partielles ∂z/∂x et ∂z/∂y de z par rapport à x et y sont supposées continues sur le domaine d'étude (inclus dans R2).
La fonction inconnue apparaît dans l'expression des coefficients a, b et c. En recherchant une fonction z = f(x,y) sous une forme implicite φ(x,y,z) = 0 vérifiant (e), on simplifie quelque peu le problème en obtenant une équation d'inconnue φ dont les coefficients a, b et c ne dépendent plus directement de l'inconnue. En effet, φ(x,y,z) = 0 étant identiquement nul, les dérivées totales de φ par rapport à x et y sont nulles :

ce qui conduit, en reportant dans (e), à une équation homogène (c.-à-d. sans second membre) :

L'étude générale des systèmes différentiels conduit à résoudre le système caractéristique de l'équation :

et la recherche des intégrales premières permettra, dans ce cas relativement simple (équation linéaire du 1er ordre), de connaître la solution générale de l'équation proposée sous une forme F(ψ1,ψ2) où F est cependant arbitraire, ψ1 et ψ2 désignant deux intégrales premières. Sur ce difficile sujet, nécessitant de longs développements préliminaires (systèmes différentiels, intégrales premières, équations du second ordre), les liens ci-après permettront d'éclairer le sujet avec rigueur et précision (niveau maîtrise).
» Heaviside , Galerkin , Hörmander , Villani , Nash
➔ Pour en savoir plus :
Cours de mathématiques,
Tome 2, par Jean Bass, Éd. Masson et Cie - Paris, 1964.
Méthodes mathématiques pour les sciences physiques,
par Laurent Schwartz.
Éd. Hermann,1965. On y trouvera la résolution des équations des cordes vibrantes, des membranes vibrantes et
de la chaleur dans le cadre
de la théorie des
distributions.
Vidéo
: Henri Poincaré et les équations aux dérivées partielles
(univ. Lorraine) :
http://numerique.univ-lorraine.fr/mediatheque/sciences-et-societe/Henri-Poincare-et-les-equations-...
Sur les méthodes d'approximations successives (pour
les EDP) par Émile Picard (1898) :
https://www.jstor.org/stable/2369869?seq=1#metadata_info_tab_contents