ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
|
D'origine française, Simon Antoine Jean L'Huilier (ou Lhuillier) était protestant et sa famille avait dû fuir la France pour se réfugier en Suisse après la révocation de l'Édit de Nantes (1691). Il naquit et étudia à Genève à l'Académie Calvin. En 1777, il se rend en Pologne où il fut, onze années, le tuteur du fils du prince Adam Czartoryski.
En 1786, il est correspondant de l'Académie impériale de Russie et de la société d'éducation de Pologne. Il se fait brillamment remarquer cette année là par son mémoire sur le calcul infinitésimal, Exposition élémentaire des principes des calculs supérieurs pour servir de réponse à la demande d'une théorie claire et précise de l'infini mathématique, qui lui vaut cette année là le prix de l'Académie des sciences de Berlin (en ligne sur le site Gallica de la BnF).
Une abréviation bien pratique :
Dans son mémoire sur le calcul infinitésimal, il développe le concept de limite pour lequel il apporte une notation nouvelle bien pratique : l'abréviation lim. pour limite. Cela peut paraître banal aujourd'hui, mais l'introduction de cette abréviation allégea considérablement les traités d'analyse :
» d'Alembert et le concept de fonction dérivée
La présence sous le signe lim du comportement de la variable, par exemple lorsque h → o comme ci-dessous :
ne fut utilisée qu'ultérieurement par Weierstrass vers 1850. Avant cette date, on précisait ce comportement dans le contexte, ce qui le rendait assez lourd, voire indigeste...
➔ Outre quelques papiers sur les probabilités relatifs à la probabilité des causes, L'Huilier s'intéressa aussi à la géométrie des polyèdres, proche des problèmes des futurs développements de la topologie combinatoire en apportant (1813) un complément à la formule de Descartes-Euler établie pour les polyèdres convexes :
S - A + F = 2 - 2p où p est le nombre de "trous" du polyèdre considéré.
Cette généralisation de la formule de Descartes-Euler apparaît comme un invariant topologique et un outil pour la classification des surfaces. Ci-dessous, ce polyèdre, homéomorphe à un tore, vérifie S - A + F = 0 : c'est sa caractéristique.
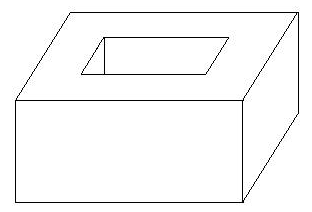
Notion de topologie combinatoire : »
Mascheroni
L'HUILLIER Simon
Antoine Jean,
suisse, 1750-1840