ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Formes multilinéaires       » déterminant d'ordre 2 | changement de base |        Formes trilinéaires et déterminant d'ordre 3 | déterminant mineur | inversion d'une matrice

 i  Cette page suppose connues les notions d'application linéaire, de forme linéaire et de matrice d'application linéaire :

Quel que soit le niveau traité, l'objectif de ChronoMath n'est pas d'écrire un manuel de cours. Pour cette raison, l'approche des déterminants est ici faite de façon progressive afin d'être comprise par le plus grand nombre de lecteurs intéressés par les mathématiques : ordre 2, formes bilinéaires alternées, puis ordre 3, formes trilinéaires alternées. Les propriétés remarquables des déterminants, rencontrées ci-dessous, se généralisent à toute dimension : formes multilinéaires alternées.

E, F et G sont des espaces vectoriels sur un même corps commutatif K. Une application f : (u,v) → f(u,v), définie de E × F vers G, est dite bilinéaire si elle est linéaire par rapport u et v. En d'autres termes si :

• 1. ∀ v∈F, l'application f_v: u → f(u,v) est linéaire de E vers G
• 2. ∀ u∈E, l'application f_u: v → f(u,v) est linéaire de F vers G

Les applications f_u et f_v sont souvent appelées applications partielles associées à f (ces dénominations s'appliquent à toute fonction de plusieurs variables).

• On a, en particulier, avec des notations évidentes : f(0_E,0_F) = 0_G ainsi que f(x,0_F) = f(0_E,y) = 0_G.

Si E = F, on parle d'application bilinéaire sur E à valeurs dans G; et si G = K, une application bilinéaire prend le nom de forme bilinéaire sur E.

• L'application Φ qui à tout couple d'endomorphismes de E, associe g o f, est une application bilinéaire de E × E dans E.

• Le corps R des réels étant considéré comme espace vectoriel sur lui-même, l'application f de R × R dans R, définie par f(x,y) = xy est une forme bilinéaire.

 ➔  On prendra garde de ne pas confondre une application bilinéaire E × F vers G avec une application linéaire de E × F vers G ! Par exemple : dans le cas E = F = G = R : considérer f(x,y) = x. Cette application est linéaire : f[a(x,y) + b(x',y')] = f(ax + bx',ay + by') = ax + bx' = a.f(x,y) + b.f(x',y'). Mais cette application n'est pas bilinéaire car f_x est l'application constante y → x qui n'est linéaire que si x = 0. Remarquer cependant que f_y est l'application identique x → x : elle est linéaire.

Une application bilinéaire sur E à valeurs dans G est dite :

• symétrique, si pour tout couple (u,v) : f(u,v) = f(v,u).
• antisymétrique, si pour tout couple (u,v) : f(u,v) = -f(v,u).
• alternée : si pour tout vecteur u de E : f(u,u) = 0_G (= 0, élément nul de K lorsque f est une forme).
  Dans le cas multilinéaire f s'annule si deux des vecteurs u, v, w, ... qui la composent sont égaux (ou colinéaires).

Une forme bilinéaire sur E, à valeurs dans K d'élément nul 0, est dite :

• positive : pour tout vecteur u de E : f(u,u) ≥ 0.
• définie ou non dégénérée : pour tout vecteur u de E : f(u,u) = 0  ⇔  u = 0_E.

Par exemple :   

1. Soit E un plan vectoriel réel (K = R) rapporté à une base (i,j), posons u = x.i + y.j et v = x'.i + y'.j et f(u,v) = xx' + yy'. On définit ainsi une forme bilinéaire symétrique définie positive sur E. On reconnait là le produit scalaire "classique" du plan vectoriel euclidien.

2. Avec les notations de 1, posons cette fois f(u,v) = xy' - yx'. On reconnait là le déterminant d'un couple de vecteurs du plan : forme bilinéaire antisymétrique alternée.

3. Toujours avec les notations de 1, posons cette fois f(u,v) = xx' - yy'. Nous avons là une forme bilinéaire symétrique sur E. Elle est dégénérée non positive : f(u,u) = x² - y² = 0  pour tout x = ± y.

4. En dimension 3, le produit vectoriel usuel est une application bilinéaire antisymétrique et alternée.

Lorsque f(u,v) = 0, par analogie avec le produit scalaire euclidien (» ci-après), on dit que u et u sont orthogonaux relativement à f.

La forme q : u→ f(u,u) est appelée forme quadratique associée à f.

∗∗∗
Une telle forme q sur E n'est pas linéaire : q(λu) ≠ q(λu). En effet, q(λu) = f(λu,λu) = λf(u,λu) = λ²f(u,u) = λ²q(u).
En calculant q(u+v) = f(u+v,u+v), on vérifiera que q est additive à condition que f soit antisymétrique.

En savoir plus sur les formes quadratiques : »

Vecteur isotrope :    

f désignant une forme bilinéaire sur E, on qualifie de vecteur isotrope pour f (du grec iso = même et tropos = direction, terme initié par Cauchy en 1840), tout vecteur u de E tel que f(u,u) = 0, ce qui revient à dire q(u) = 0. Lorsque f admet le seul vecteur nul comme vecteur isotrope, f est dite anisotrope (du grec a, an = préfixe privatif). Il en est ainsi de f lorsqu'elle définit un produit scalaire (» ci-après).

Si u est isotrope pour f, tout vecteur colinéaire à u est isotrope pour f puisque f(λu,λu) = λ²f(u,u) = 0. Par suite, l'ensemble des vecteurs de la droite vectorielle engendrée par u est isotrope : on parle de droite isotrope de direction u. L'ensemble des droites isotropes "passent par" 0_E : on parle de cône isotrope pour f.

• Avec les notations de l'exemple 1, la forme f(u,v) = xx' - yy' bilinéaire, symétrique, dégénérée non positive, admet deux familles de vecteurs isotropes définies par x = ± y, donc engendrées par i + j d'une part et i - j d'autre part.

∗∗∗
1. En calculant f(u-u,u-u), montrer que si f est antisymétrique, tout vecteur de E est isotrope pour f.
2a. En calculant f(u+v,u+v), montrer que si f est alternée, elle est également antisymétrique.
2b. à l'exception du cas où le corps de scalaires K est de caractéristique 2, montrer que toute application bilinéaire antisymétrique est alternée.

∗∗∗  
Cinq petits exos de gymnastique bilinéaire

Produit scalaire :    

On appelle ainsi une forme bilinéaire symétrique et positive sur un espace E.

Lorsque la forme est, de plus, non dégénérée, on parle d'espace vectoriel euclidien car on retrouve la définition du produit scalaire dans le plan et l'espace de la géométrie euclidienne élémentaire.

En savoir plus sur le produit scalaire : »  

Produit vectoriel :    

Dans l'espace euclidien usuel (dimension 3), le produit vectoriel est une application bilinéaire antisymétrique et alternée.

En savoir plus sur le produit vectoriel : »

Les écritures en gras désignent des vecteurs. x, y, z, x', ... désignent des éléments de K (coordonnées, coefficients). On suppose E de dimension finie n. Considérons tout d'abord deux cas élémentaires :

a/  dimE = 2 et E est rapporté à la base (i,j). Posons u = x.i + y.j et v = x'.i + y'.j. On a alors par bilinéarité :

f(u,v) = f(x.i + y.j , x'.i + y'.j) = f(x.i, x'.i + y'.j) + f(y.j , x'.i + y'.j)
         = xx'.f(i,i) + xy'.f(i,j) + yx'.f(j,i)+ yy'.f(j,j)

Mais f étant symétrique, on a f(i,j) = f(j,i), donc :

b/  dimE = 3 et E est rapporté à la base (i,j,k). Posons u = x.i + y.j + z.k et v = x'.i + y'.j + y'.k. On obtient de même par bilinéarité :

f(u,v) = f(x.i + y.j + z.k , x'.i + y'.j + z'.k)
         = f(x.i, x'.i + y'.j + z'.k) + f(y.j, x'.i + y'.j + z'.k) + f(z.k, x'.i + y'.j + z'.k)
         = xx'.f(i,i) + xy'.f(i,j)  + xz''.f(i,k) + yx'.f(j,i) + yy'.f(j,j) + ... + zy'.f(k,j) + zz''.f(k,k)

On voit ainsi, d'une façon générale :

Une forme bilinéaire sur E est définie par l'image des couples des vecteurs d'une base de E

Afin de généraliser, on peut écrire : u de coordonnées x₁, x₂, x₃, ..., x_n au lieu de x, y, z, ..., v de coordonnées x'₁, x'₂, x'₃, x'_n au lieu de x', y', z', ..., et e₁, e₂, e₃, ... au lieu de i, j, k, ... : la matrice de la forme bilinéaire symétrique f est alors :

M = (a_ij) avec a_ij = f(e_i,e_j) et a_ij = a_ji

C'est donc une matrice symétrique : les éléments placés symétriquement par rapport à la diagonale sont égaux. Le rang de cette matrice (dimension du s. e. v. engendré par ses vecteurs-colonnes) est le rang de la forme bilinéaire f. Ce rang est indépendant de la base choisie. On a :

L'ensemble des formes bilinéaires sur E est un espace vectoriel. Elles sont complètement déterminées par la donnée des f(e_i,e_j) : sa dimension est donc n². Les formes bilinéaires symétriques sur E constituent elles aussi espace vectoriel. Elles sont complètement déterminées par la donnée des f(e_i,e_i) et des f(e_i,e_j) pour i < j car on peut écrire :

La symétrie permet d'affirmer que sa dimension est n + (n² - n)/2 = n(n + 1)/2.

En notant encore u et v les matrices unicolonnes des coordonnées de u, la matrice transposée ^tu est la matrice ligne des coordonnées. On peut alors écrire :

Soit, plus explicitement :

Formes quadratiques : »

P désignant un plan vectoriel (espace vectoriel de dimension 2) sur un corps commutatif K, on note B = (i,j) une base de P. On appelle déterminant dans la base B, la forme bilinéaire et alternée sur P telle que f(i,j) = 1. On a donc, en notant V(x,y) et W(x',y') un couple de vecteurs de P exprimés dans la base B :

Au lieu de f, on note généralement det_B un déterminant; on omet B s'il n'y a pas d'ambiguïté et selon la notation de Cauchy, on écrit :

 ➔  Noter que, par linéarité que det_B(V + k.W,W) = det_B(V,W + k.V) = det_B(V,W).

Le déterminant d'un couple de vecteurs (bivecteur) dépend de la base choisie pour l'exprimer. Mais sa nullité n'en dépend pas : la relation (det) ci-dessus montre que l'ensemble des formes bilinéaires alternées sur P est un espace vectoriel sur K de dimension 1. Si B' est une seconde base de P, il existe donc un scalaire k non nul de K tel que :

Or det_B'(B') = 1, donc k = det_B(B'). C'est dire que si B et B' sont deux bases de P, alors det_B = det_B(B').det_B'. En particulier : det_B'(B) x det_B(B') = 1, ou encore :

Déterminant d'une matrice carrée :

Si est une matrice carrée d'ordre 2, on appelle déterminant de M le nombre ad - bc et on écrit :

Lorsque M est la matrice, relativement à B, d'un endomorphisme f,  f est bijective (automorphisme) si et seulement si det M ≠ 0 et on vérifie facilement que la matrice de l'application réciproque f^-1 est, relativement à B, la matrice notée M^-1 :

telle que M × M^-1  = M^-1 × M^-1 = I, où I désigne la matrice unité , élément neutre de la multiplication matricielle.

Dans le cas d'un système linéaire 2 × 2 :

on aura :

        » matrice inverse : cas général

Voici un résultat fondamental :

Soit f un endomorphisme de P et M_B la matrice de f dans une base B; on appelle déterminant de f, et on note det(f), le déterminant de la matrice M_B et ce déterminant, contrairement à celui d'un bivecteur, ne dépend pas de la base B choisie.

Preuve : pour tout forme bilinéaire alternée φ, notons h : (v,w) → φ(f(v),f(w)). On définit ainsi manifestement une forme bilinéaire alternée sur P. L'application H_f qui à φ associe h donc linéaire dans l'espace vectoriel A des formes bilinéaires alternées sur P; cet espace étant de dimension 1, H_f est donc une homothétie de P dont le rapport , par définition de H_f , ne dépend que de f. Soit k ce rapport : pour toute forme φ, on a donc H_f (φ) = k.φ et on peut calculer k en choisissant φ = det_B où B est une base (i,j) de P. On a d'une part : [H_f (det_B)](i,j) = det_B[f(i),f(j)] = det(M_B) et, d'autre part : [H_f (det_B)](i,j) = k.det_B(i),j) = k.det_B(B) = k × 1 = k. Le scalaire k ne dépendant que de f, det(M_B) = k, ne dépend pas de B.

 i  Remarque : on vient de montrer aussi que si f est linéaire et si φ est une forme bilinéaire alternée quelconque, on a :

1. f et g désignant deux endomorphismes de P, montrer que :

• i/ det(k.f) = k².det(f) pour tout scalaire k de K.
• ii/ det(f o g) = det(f) x det(g);
  utiliser la remarque ci-dessus en écrivant que det(f o g) n'est autre que det_B[f(g(i)),f(g(j))] où B est une base quelconque de P.
• iii/ si id_P désigne l'application identique de P : id_P(v) = v pour tout v de P, alors det(id_P) = 1;
• 4i/ si f est bijective, alors det(f^-1) = 1/det(f).
• 5i/  !   il n'y a pas de formule pour le déterminant d'une somme f + g : ce n'est PAS det(f) + det(g).

On déduit de ces résultats des égalités semblables relatives matrices des endomorphismes considérés comme :

2. On considère le système d'équation ax + by = m , cx + dy = n

• i/ donner une écriture matricielle de la forme MX = K de ce système où X et K sont des matrices colonnes;
• ii/ prouver qu'il admet une unique solution (x,y) ssi detM = ad - bc est non nul;
• iii/ lorsque det M ≠ 0, montrer que x = det_x/detM , y = det_y/detM avec :

Cas général : Système de Cramer , Théorème de Rouché-Fontené & déterminants caractéristiques

3. On considère la fonction rationnelle f définie par :

Montrer que la fonction dérivée peut s'écrire :

E désignant un espaces vectoriel sur un corps commutatif K qui sera ici R ou C. Une forme f : (x,y,z) → f(x,y,z), de E vers K, est dite trilinéaire si elle est linéaire par rapport à x, y et z. En d'autres termes :

les applications f_yz : x → f(x,y,z), f_zx : y → f(x,y,z) et f_xyz : z → f(x,y,z) sont linéaires.

• Si V(x₁,x₂,x₃), W(y₁,y₂,y₃) et Z(z₁,z₂,z₃) sont des vecteurs de E exprimés dans une base B = (e₁,e₂,e₃), alors :
          → 27 termes !

En effet, par linéarité par rapport à V :

Or, W = Σy_j.e_j , par suite :

On a donc :

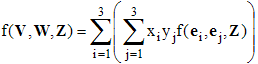
Et on arrive au résultat annoncé en utilisant de la même manière la linéarité par rapport à Z.

 ➔  Une forme trilinéaire est dite alternée si elle s'annule lorsque 2 au moins des vecteurs x, y et z sont égaux. Comme en dimension 2, une telle forme est aussi antisymétrique, en échangeant la place de deux vecteurs dans le triplet (V,W,Z), la forme change de signe.

• Pour s'assurer de cela, calculer f(V + W,V + W,Z).

Si B = (i,j,k) est une base de E, on appelle déterminant dans la base B, l'unique forme trilinéaire alternée f vérifiant f(i,j,k) = 1. Comme dans le cas de la dimension 2 (déterminant d'ordre 2), on note det_B plutôt que f.

Si V(x,y,z), W(x',y',z') et Z(x",y",z") sont des vecteurs de E exprimés dans la base B, alors :

» Noter que, par linéarité que det_B(V + k.W,W) = det_B(V,W + k.V) = det_B(V,W). Cette propriété permet de simplifier le calcul de déterminants en faisant apparaître, par combinaison linéaire, des zéros dans les colonnes.

 ➔  Dans le calcul du déterminant d'ordre 3, il ne reste que les coefficients des six permutations de (i,j,k). si l'une vaut k, les autres vaudront k ou -k. C'est dire que l'ensemble des formes bilinéaires alternées sur E est un espace vectoriel sur K de dimension 1. Ceci montre ici encore que le déterminant d'un triplet de vecteurs (trivecteur) dépend de la base choisie pour l'exprimer et on a,  comme en dimension 2 :

Les définitions et résultats vus en dimension 2 se retrouvent en dimension 3. En particulier :

∗∗∗
f et g désigne deux endomorphismes de l'espace vectoriel E sur K de dimension 3.
Montrer que det(k.f) = k³.det(f) pour tout scalaire k de K
Les points ii/, iii/ et 4i/ de la dimension 2 sont encore valables (en toute dimension d'ailleurs) et on déduira de ces résultats des égalités
semblables en passant aux matrices des endomorphismes considérés.

Étant donné une matrice carrée M = (a_ij), on appelle déterminant mineur (ou simplement mineur) du terme a_ij, le déterminant d_ij de la matrice obtenue en supprimant la ligne i et la colonne j de M.

 i  Afin que cette définition soit générale, on accepte d'appeler déterminant d'ordre 1 un scalaire quelconque. Cela revient à poser, pour toute droite vectorielle (espace vectoriel de dimension 1) engendrée par un vecteur u, det_u(V) = k, dès lors que V = ku.

Dans ces conditions, on démontre que la matrice inverse de M = (a_ij) peut s'obtenir de la façon suivante :

• 1. Calculer le déterminant D de la matrice M;
• 2. Remplacer chaque élément a_ij de M par son mineur d_ij;
• 3. Multiplier chaque terme de la matrice (d_ij) obtenue par (-1)^i+j;
• 4. Transposer la matrice obtenue, c'est à dire échanger le rôle des lignes et des colonnes : la ligne k devient la colonne k.
• 5. Diviser la matrice obtenue par D.

 ➔  Pour en savoir plus :

• Tout cours d'algèbre linéaire niveau DUES, Classes préparatoires.
  En particulier : Algèbre générale, B. Charles, Denis Allouch, Éd. Presses universitaires de France - Paris, 1984.