ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Application linéaire tangente & différentielle d'une fonction     Approximation locale d'une fonction          » Cas de plusieurs variables , différentielle d'ordre n

Si f est une fonction numérique dérivable en un point x_o, on dit aussi, de façon équivalente, qu'elle est différentiable en x_o : reprenons la définition du nombre dérivé f'(x_o) obtenue en posant h = x - x_o dans l'écriture du taux d'accroissement de f en x_o :

Lorsque ce nombre existe, on peut donc écrire qu'il existe une fonction h → ε(h) de limite 0 lorsque h tend vers 0 telle que :

f(x_o + h) =  f(x_o) + h[f'(x_o) + ε(h)]

On sait que l'équation de la tangente à la courbe est donnée par :

y_T = f(x_o) + (x - x_o)f'(x_o) = f(x_o) + hf'(x_o) avec h = x - x_o.

En comparant ces deux dernières égalités, on voit que l'ordonnée d'un point de la tangente en x_o approche la fonction f au point x_o + h à hε(h) près, quantité d'autant plus petite que h est petit :

 f(x_o) + hf'(x_o) ≅ f(x_o + h)

L'application h → hf'(x_o) définie au voisinage de x_o est une fonction linéaire de h. Pour les raisons ci-dessus, elle est appelée application linéaire tangente au point x_o.

 ➔  Depuis Leibniz, génial précurseur, avec Newton, du calcul différentiel, lorsque h est infiniment petit, on le note traditionnellement dx. L'application h → hf'(x_o) s'écrit alors

dx → dx × f'(x_o) = f'(x_o)dx

et prend le nom de différentielle de f au point x_o. On peut utiliser différentes notations suivant le contexte :

• df_xo = f'(x_o)dx  ou  df(x_o) = f'(x_o)dx

• df = f'(x)dx (en un x quelconque) ou, si on a noté y = f(x) : dy = f'(x)dx

∗∗∗
Donner une approximation de la racine carrée de 3,07 sachant que √3 ≅ 1,732.
                 Rép : sachant aussi que  (√x)' = 1/2 √x, on a trouve, avec h = 0,07 ≅ 1,75225. Val. exacte : 1,75214.

 ! On exprime souvent la différentielle d'une fonction numérique par df = f'(x)dx en partant du fait que si x est suffisamment petit, pour un petit accroissement Δx de x, on a sensiblement Δy/Δx = f'(x) et donc, pour x infinitésimal, il serait alors licite de poser conventionnellement df/dx = f'(x). Ce n'est pas tout à fait cela...

Dans le calcul de f'(x), si ce nombre existe, le taux d'accroissement s'écrit en effet Δy/Δx. Mais lorsque Δx devient infiniment petit pour obtenir f'(x), c'est pour tendre vers 0 et il doit en être de même de Δy. On obtient donc à la limite une forme 0/0 qui ne peut en aucun cas s'écrire dy/dx, à moins que dx et dy ne soient nuls !

Le calcul précédent : f(x_o + h) = f(x_o) + h[f'(x_o) + ε(h)] montre que Δy = Δxf'(x_o) + Δxε(Δx). Interprétons graphiquement :

On a tracé la tangente (t) en M(x,y) d'une fonction y = f(x) dérivable en x. Le coefficient directeur de cette tangente est f'(x). C'est aussi tan(^KMT) = KT/MK. On voit dans ces conditions que dans la notation différentielle dy = f'(x)dx, lorsque dx joue bien le rôle infinitésimal d'un Δx non nul mais aussi petit que l'on voudra, il n'en est pas de même de dy :

dy = f'(x)dx = KT/MK × MK = KT ≠ KN  , KT jouant le rôle de Δy !

Le calcul a montré que la différence algébrique entre dy et Δy est Δxε(Δx), cela représente donc NT.

On constate, et cela est tout à fait fondamental, eu égard à l'histoire de la notation différentielle puisant sa genèse dans les sciences physique, que :

 ➔  Utiliser la différentielle d'une fonction consiste à estimer que sur un intervalle extrêmement petit dx, la variation df de la fonction f est proportionnelle à cet intervalle dans le rapport f '(x).

On constate son utilisation pour de nombreux phénomènes physiques ou la variable principale est le temps :

∗∗∗  Exemples concrets d'équation différentielle

On se restreint ici à une fonction numérique (à valeurs dans R) de 2 variables, la généralisation à n variables se fait relativement facilement. Soit donc (x,y) → f(x,y) une fonction de numérique de deux variables indépendantes x et y, définie dans un domaine A × B de R². On suppose que f admet des dérivées partielles continues du 1er ordre en x et y au voisinage d'un point (x_o,y_o) de A × B : f est dite continûment différentiable.

Plaçons-nous en un point (x_o + h, y_o + k) "proche" de (x_o,y_o), h et k pouvant être de signes quelconques, et étudions l'accroissement correspondant de f, à savoir :

Δf = f(x_o + h, y_o + k) - f(x_o,y_o)

Δf peut s'écrire :

 Δf = [ f(x_o + h, y_o + k) - f(x_o, y_o + k) ] + [ f(x_o, y_o + k) - f(x_o,y_o) ]

Le 1er crochet s'interprète comme l'accroissement de f en (x_o, y_o + k) lorsque x s'accroît de h; le second membre s'interprète comme l'accroissement de f en (x_o, y_o) lorsque y s'accroît de k. On peut alors appliquer la formule des accroissements finis à chaque crochet : il existe θ_x et θ_y de l'intervalle [0,1] tels que :

Considérons alors h et k infiniment petits. Il en sera de même de θ_xh et θ_yk et la continuité des dérivées partielles en (x_o,y_o) permet d'écrire qu'il existe deux fonctions h → ε(h)  et  k → ε'(k) tendant vers 0 avec h et k telles que :

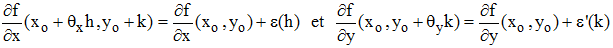
D'où :

Différentielle totale :     

En reprenant la notation traditionnelle dx = h et dy = k : on appelle différentielle totale de f au point (x_o,y_o) le nombre :

et, plus généralement, on notera :

On parle de différentielle "totale" car on a tenu compte dans ces calculs des accroissements de x et de y. Les termes de la somme sont respectivement les différentielles partielles de f par rapport à x et par rapport à y. Afin de simplifier la rédaction, on notera parfois :

ce qui permet d'écrire : df = f'_x dx + f'_y dy ou encore, avec des notations évidentes : df = df_x + df_y.

∗∗∗
Donner une approximation δ de la variation relative de f(x,y) = xy² lorsque les coordonnées x et y augmentent de 1%.
                 Rép : f '_x = y², f '_y = 2xy, dx  = x/100, dy = y/100. D'où δ ≅ df/f = 3%.

 ➔  Noter que la différentielle totale df : (h,k) → h × f'_x(x_o,y_o) + k × f'_y(x_o,y_o) est une application linéaire (une forme, plus précisément, puisque c'est un nombre) de la variable (h,k).

D'autre part, en posant z = f(x,y), on définit une surface par ses lignes de niveau. L'équation du plan tangent en un point (x_o,y_o,z_o) est alors :

z - z_o = (x - x_o)f'_x(x_o,y_o) + (y - y_o)f'_y(x_o,y_o)

Comme dans le cas d'une variable, où l'on avait y_T = f(x_o) + (x - x_o)f'(x_o) = f(x_o) + df_xo, on voit qu'au voisinage du point (x_o,y_o,z_o), on peut écrire :

z_T = f(x_o,y_o) + h × f'_x(x_o,y_o) + k × f'_y(x_o,y_o) =  f(x_o,y_o) + df_xo,yo

Ce qui justifie, là encore pour la différentielle totale de f, le qualificatif d'application linéaire tangente.

Équation de la tangente en un point d'une courbe algébrique f(x,y) = 0 :  »

Cas de plusieurs variables :   

Ces résultats se généralisent par récurrence à des fonctions de plus de 2 variables. Dans le cas de 3 variables, le calcul de la différentielle de (x,y,z) → f(x,y,z) est tout à fait semblable :

Δf = f(x_o + h, y_o + k, z_o + k) - f(x_o, y_o, z_o) =
       [f(x_o + h, y_o + k, z_o + k) -  f(x_o + h, y_o + k, z_o )] +  [f(x_o + h, y_o + k, z_o ) - f(x_o, y_o, z_o)]

Le 1er crochet s'interprète comme l'accroissement de f en (x_o + h, y_o + k, z_o) lorsque z s'accroît de k : on retrouve le calcul de la différentielle d'une fonction de variable z; le second membre s'interprète comme l'accroissement de f en (x_o, y_o, z_o) lorsque x s'accroît de h et y s'accroît de k : on retrouve le calcul de la différentielle d'une fonction de deux variables x et y. D'où, si les dérivées partielles de f existent et sont continues au voisinage du point considéré :

df = f'_x(x, y, z) × dx + f'_y(x, y, z) × dy  + f'_z(x, y, z) × dz

I - Cas d'une variable :  

La différentielle df d'une fonction f est une fonction de x : df = f'(x)dx et dans cette notation, dx représente une quantité infinitésimale dx = h qui doit être regardé comme une constante. df est une fonction de x que l'on peut différencier : ce sera la différentielle seconde de f, notée symboliquement d²f :

d²f = d[f'(x)dx] = dx × d[f'(x)] = dx × [f''(x)dx]  = (dx)² × f''(x)

 !   Conventionnellement (dx)² est noté plus simplement dx² mais, attention, ce n'est pas la différentielle de x² qui serait alors 2xdx ! Ce calcul et cette notation justifient la notation usuelle :

f''(x) = d²f/dx²

On peut généraliser ce résultat à une différentielle troisième d³f,..., voire n-ème dⁿf (on dit aussi d'ordre n).  f⁽ⁿ⁾ désignant la dérivée n-ème de f (quand elle existe !) :

dⁿf = f ⁽ⁿ⁾(x)dxⁿ

Et, là encore, ce résultat justifie la notation usuelle f ⁽ⁿ⁾(x) = dⁿf/dxⁿ.

II - Cas de 2 variables :  

f étant une fonction deux fois continument dérivable par rapport à x et y :

df est une fonction de x et y dont on peut calculer la différentielle : ce sera la différentielle seconde de f, notée symboliquement d²f . Dans ce calcul, les quantités infinitésimales h = dx et k = dy sont des constantes. Pour simplifier les écritures, on omet d'écrire (x,y) :

d²f = d(∂f/∂x × dx + ∂f/∂y × dy) = dx × d(∂f/∂x) + dy × d(∂f/∂y)

Or, d(∂f/∂x) =  ∂²f/∂x² × dx + ∂²f/∂x∂y × dy  et  d(∂f/∂y) =  ∂²f/∂y∂x × dx + ∂²f/∂y² × dy. L'hypothèse sur f permet d'égaliser les dérivées partielles ∂²f/∂x∂y et ∂²f/∂y∂x (théorème de Schwarz), d'où :

d²f =  ∂²f/∂x² × dx² + 2∂²f/∂x∂y × dxdy + ∂²f/∂y² × dy²

On remarque les coefficients 1, 2, 1 et une forme pouvant s'écrire symboliquement :

d²f =  (∂/∂x × dx + ∂/∂y × dy)⁽²⁾ f

 ➔   (∂/∂x × dx + ∂/∂y × dy)⁽²⁾ apparaît ainsi comme un opérateur (linéaire).

De même, d²f est une fonction de x et y dont on peut calculer la différentielle : ce sera la différentielle troisième de f, notée symboliquement d³f. Et un petit calcul calqué sur le précédent permettra de montrer que si f est de classe C³ (admettant des dérivées partielles continues d'ordre 1, 2 et 3 par rapport à chaque variable) :

d³f =  ∂³f/∂x³ × dx³ + 3∂³f/∂x²∂y × dx²dy + 3∂³f/∂x∂y² × dxdy² + ∂³f/∂y³ × dy³

On voit apparaître les coefficients 1, 3, 3, 1 de la formule du binôme et on peut écrire symboliquement :

d³f =  (∂/∂x × dx + ∂/∂y × dy)⁽³⁾ f

et on pourra admettre, d'une façon générale, pour une fonction de classe Cⁿ :

dⁿf =  (∂/∂x × dx + ∂/∂y × dy)⁽ⁿ⁾ f

La formule se généralise facilement à un nombre fini quelconque de variables.

Un usage de cette formule dans le développement de Taylor d'une fonction de 2 variables :  »

Considérons le cas d'une fonction u : x → y = u(x) non définie explicitement comme le serait u(x) = x² - 1 mais par une relation entre x et y de la forme f(x,y) = 0 : x et y ne sont pas indépendants. C'est le cas de nombreuses courbes planes où l'expression de y en fonction de x n'est pas facilement calculable. On parle de fonction implicite.

• x² + y² - 2x + y - 0 = 0 est l'équation d'un cercle. On peut donner l'expression de y en fonction de x (resp. de x en fonction de y) en résolvant une équation du second degré où x (resp. y) intervient comme paramètre. D'où 2 cas pour l'expression de y (resp. x).

Lorsque y est fonction de x, posons z = f(x,y), f est différentiable. C'est une fonction de x dont la différentielle totale s'écrit :

On en tire la dérivée totale de z par rapport à x (par opposition à la dérivée partielle ∂f/∂x) :

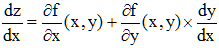
Maintenant, sachant que nous avons f(x,y) = 0 pour tout x, on a z = 0, donc dz/dx = 0 pour tout x : en omettant (x,y) pour simplifier les écritures, on peut alors écrire :

Cette formule permet d'exprimer le coefficient directeur y' = dy/dx de la tangente à la courbe définie implicitement par f(x,y) = 0 :

Dérivation implicite des 1er et second ordres :     

On peut aussi écrire la dérivée totale de f sous la forme (pratique dans la pratique...) :

f'_x + y'f'_y = 0

Posons F(x,y) = f'_x + y'f'_y et calculons la dérivée totale de cette fonction implicite. Notons tout d'abord que, dans la dérivation par rapport à y,  y' doit être regardée comme une fonction de x; par suite ∂(y'f'_y)∂y = y'∂(f'_y)∂y = y'f ''_yy. On  a alors :

Finalement :

f''_xx + 2y'f''_xy + y"f'_{y +} y'²f''_yy= 0

Tangente à une courbe définie par une fonction implicite : »

 ➔   Qu'advient-il dans le cas où  x et y sont dépendants par l'intermédiaire d'un paramètre t ?  On applique à la différentielle dz la formule élémentaire de dérivation des fonctions composées (f o g)' = f'_g × g'_x et on obtiendra :

Une expression de la forme ω = P(x,y)dx + Q(x,y)dy, qualifiée de forme différentielle, a peu de chances d'être la différentielle totale d'une fonction (x,y) → f(x,y) ! Lorsque c'est le cas, on parle d'ailleurs de différentielle exacte...

Considérons la fonction f(x,y) = 3xy²  - 5xy. On a ici f'_x(x,y) = P(x,y) = 3y² - 5y et f'_y(x,y) = Q(x,y) = 6xy - 5x.

On remarque que P'_y(x,y) =  6y - 5 = Q'_x(x,y). Ce n'est pas un hasard ! On montre en effet que :

• Dans R² : P(x,y)dx + Q(x,y)dy est une différentielle exacte si et seulement si, pour tout (x,y), P'_y(x,y)  = Q'_x(x,y).
  Autrement écrit :

• Dans R³ : P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz est une différentielle exacte si et seulement si

P'_y(x,y,z)  = Q'_x(x,y,z),  Q'_z(x,y,z)  = R'_y(x,y,z) et  R'_x(x,y,z)  = P'_z(x,y,z)

Autrement écrit :

» cela revient à dire que le rotationnel de V(P,Q,R) est nul.

On démontre que si  ω est une forme différentielle de classe C¹ sur un ouvert U de R² ou R³, ω est une différentielle exacte si et seulement si l'intégrale curviligne :

∫_Γ ω

est nulle pour toute courbe Γ fermée dans U.

Longueur d'arc et intégrale curviligne : »             Différentielles exactes et intégrales curvilignes : »