ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 LAMBERT Jean Henri (Johann Heinrich), suisse,
1728-1777» Projection Lambert |
Philosophe,
physicien et astronome. Né à Mulhouse, ville alors
rattachée à la Suisse. Il invente la
"photométrie" (du grec phôs, phôtos = lumière, étude quantitative du rayonnement
lumineux) et en précise les premières lois. Travaux en
trigonométrie sphérique. Résultats sur les
coniques et les trajectoires paraboliques à travers son
Traité des comètes.
En 1764, Lambert s'installera à l'Académie des sciences de Berlin à la demande de Frédéric II (le Grand), roi de Prusse. Il sera le premier à émettre l'idée du zéro absolu et à en donner la valeur : environ -273° C.
» C'est
l'agitation des particules (électrons, atomes,
molécules) d'un corps qui détermine sa
température. Plus elles sont agités, plus le corps est
chaud. Le
zéro absolu
correspond à un état
limite de la matière : agitation nulle. il correspond à
environ -273° Celsius.
L'unité légale de
température est aujourd'hui le degré Kelvin
(physicien anglais,1824-1907).
La correspondance avec l'échelle thermométrique de
Celsius (physicien et astronome,1701-1744) est T°K = T°C +
273,15.
La trigonométrie
hyperbolique :
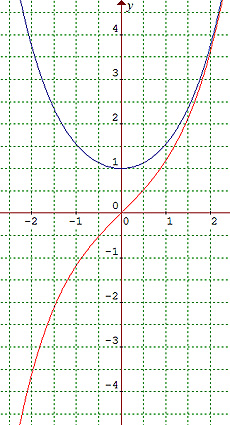Lambert développa la trigonométrie
hyperbolique (1768) en étudiant les propriétés
des fonctions numériques ch x (ou cosh x, cosinus hyperbolique) ,
sh x (ou sinh x,
sinus hyperbolique)
et th x = sinh x/cosh x (ou tanh x, tangente hyperbolique) dont la paternité et les
premiers résultats reviennent à l'italien
Vicenzo Riccati et auquel les notations sinh et cosh
sont dues :
,
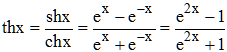
Par opposition aux angles "naturels" vérifiant cos2x + sin2x = 1, basés sur le cercle d'équation x2 + y2 = 1 et conduisant aux fonctions dites circulaires sinus et cosinus, cette trigonométrie fut dénommée hyperbolique car :
et x2 - y2 = 1 est l'équation, dans un repère orthonormé, d'une hyperbole équilatère.
Approche hyperbolique des fonctions cosinus, sinus et tangente hyperboliques : »
➔ L'usage des expressions (ex ± e-x)/2 se retrouve chez Euler avec la géniale introduction de la notation :
eix = cosx + isinx
ainsi que chez les Bernoulli et l'usage de la chaînette.
» Vincenzo Riccati En savoir plus sur sinus, cosinus et tangente hyperbolique : »
| Preuve de l'irrationalité de π (1761) : |
C'est dans un mémoire publié en l'Académie des Sciences de Berlin que Lambert prouva, reprenant des travaux de Euler et de Brouncker sur les fractions continues, l'irrationalité du nombre π : Mémoire sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, 1761.
Archimède et le périmètre du cercle : »
Lambert montra que si, dans le développement d'un nombre, la suite des réduites est finie, alors ce nombre est rationnel et le développement s'arrête. Un développement infini est la preuve d'un nombre irrationnel. Pour prouver l'irrationalité de π, Lambert développa en fraction continue illimitée, pour tout x rationnel non nul, la fonction tangente hyperbolique :
,
à savoir :
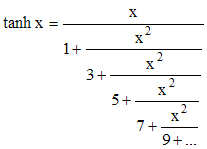
Mais, depuis Euler, on sait que eix = cos x + i.sin x et on peut donc écrire :
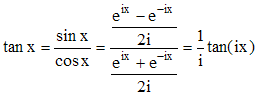
D'où :
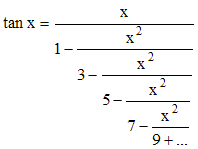
Par conséquent, si x est rationnel non nul, alors tan x est irrationnel. Mais tan(π/4) = 1 : nombre rationnel. Il suit (par contraposition) que π/4 est irrationnel, et par là que π l'est aussi. On lui doit d'ailleurs, après Oughtred et Euler, cette notation définitive (1766) pour le rapport de la circonférence à son diamètre.
Lindemann (transcendance de π) : » Calculs de π dans ChronoMath : »
➔ Le développement en fraction continue de tanh x montre aussi l'irrationalité de e2x, donc de ex, pour tout x rationnel distinct de 0. Utilisant le développement ci-dessus de tan x, Legendre montra (1792) l'irrationalité de π2. Concernant ln x, lorsque x est rationnel distinct de 1, en supposant que ln x = r est rationnel, on déduit x = er est irrationnel : ce qui est contradictoire.
Autre conséquence :
ln x est irrationnel pour tout x rationnel distinct de 1
En effet, supposons ln x rationnel pour un rationnel x strictement positif autre que 1 et posons y = ln x. Dans ces conditions, x = ey, et y étant rationnel, x doit être irrationnel, ce qui est contradictoire.
Baker : » Hermite et transcendance de e : »
| Travaux géométriques, projection Lambert : |
En géométrie, Lambert étudia les géométries non euclidiennes (Théorie des parallèles, 1766), proposa une représentation de l'espace annonçant la géométrie descriptive de Monge et inventa :
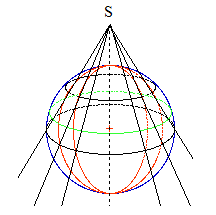
La
projection Lambert (1772), utilisée
en cartographie (légale en France) : c'est une projection
conique conforme (perspective respectant les angles) : les
méridiens sont des droites convergeant vers le centre S de
projection, sommet du cône (le méridien de base
étant celui de Paris), les parallèles (i.e. les cercles
de la sphère terrestre perpendiculaires à l'axe
Nord-Sud) sont des arcs de cercle de centre S.
Afin de préserver les angles sur la carte, la distance séparant les parallèles est augmentée en tenant compte de l'éloignement par rapport au parallèle de base sur lequel s'appuie le cône (dans le cas d'une projection conique tangente.
On utilise aussi des projections coniques sécantes : le cône contient deux parallèles. La projection Lambert altère les distances mais dans une faible mesure : suivant la zone à représenter on change les parallèles sur lesquels s'appuie le cône.
| Statistique : |
On doit à Lambert une première approche (Photometria,1760) de la méthode dite aujourd'hui du maximum de vraisemblance, dans l'estimation d'un paramètre d'une variable aléatoire étudiée sur la seule donnée d'un échantillon statistique et qu'affineront Gauss et principalement Fischer.
➔ Pour en savoir plus :
Le site de Thierry Hatt, Lycée Fustel de Coulanges (Acad. Stasbourg) : http://thierry.hatt.gps.free.fr
Bougainville