
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Théorème de Cauchy-Goursat | Formule de Green | Théorème de Morera | Théorème des résidus |
On considère une fonction complexe z → f(z) avec z = x +iy et f(z) = P(x,y) + iQ(x,y). La définition de l'intégrale de f sur un arc de courbe se définit comme dans le cas réel à la manière de l'intégrale de Riemann.
Dans toute la suite, l'arc de courbe (c) sur lequel on intégrera, est supposé inclus dans domaine U simplement connexe (pas de trou !). L'arc (c) est continu, rectifiable, simple (sans point multiple), fermé ou non, et parcouru selon un sens de parcours supposé positif : celui des abscisses curvilignes croissantes. Lorsque l'arc est un chemin (segment curviligne), on parlera d'origine et d'extrémité, comme ci-contre où l'origine est A, d'affixe zo.

Lorsque B coïncide avec A, l'arc est fermé, on sera en présence d'un lacet (très souvent, dans la pratique : un cercle). On parle aussi de contour ou parfois de circuit (sans point double, car en théorie des graphes, un circuit peut posséder des points doubles) pour exprimer que (c) est une réunion fermée ∪(ck) d'arcs jouissant des propriétés ci-dessus, l'origine de (ck+1) étant l'extrémité de (ck).
➔ Un arc continu (c) peut se définir par t → z(t) = x(t) + iy(t) où x et y sont des fonctions continues de t sur un intervalle réel [a,b]. Par exemple t →1 + eit = 1 + cost + isint où t décrit [0,π] est un demi-cercle de de rayon 1, de centre K(1,0). On a en effet |z - 1| = 1 et Arg(z - 1) compris entre 0 et π. Par rectifiable, on entend dont on peut calculer la longueur : sa paramétrisation en x(t) + iy(t) exige donc que x et y soient des fonctions continument dérivables.
Longueur d'un arc : »
A l'instar des suites de Riemann, les sommes Sn s'écrivent ici :
Les zk forment une subdivision de l'arc de courbe (c) et si ces sommes admettent une limite lorsque Max |zk - zk-1| tend vers 0, on démontre que cette limite pour n infini ne dépend ni de la subdivision, ni du choix des ck. On l'appelle intégrale (curviligne) de f sur (c) et on écrira :

Lorsque (c) est fermé, un cercle par exemple : B se confond avec A après un "tour" complet, on note parfois :

Dans les Sn, on peut remplacer zk par xk + iyk . Si on pose ck = ak + i bk, on aura f(ck) = P(ak,bk) + iQ(ak,bk). En remplaçant, un calcul simple permettra d'écrire une formule fondamentale établissant que l'intégrale d'une fonction complexe sur un arc (c) se ramène au calcul de deux intégrales curvilignes.

Fonction primitive :
Soit D un domaine simplement connexe de C et (c) ⊂D, un arc de courbe continu et rectifiable d'origine zo fixé et z un point de cet arc, alors si f est holomorphe sur D, la fonction de z définie par :

est holomorphe sur D et F'(z) = f(z) : on dira, comme dans le cas réel que F est une primitive de f dans D et toute fonction G égale à F à une constante additive près est aussi une primitive de f. On a, de plus, f étant uniforme :

On trouvera en référence des exercices sur le calcul des primitives de fonctions complexes (usuelles ou non). Le logarithme et la racine carrée posent cependant problème :
Logarithme complexe, racine carrée, point critique : »
➔ Lorsque la courbe (c) peut être paramétrée au moyen d'un paramètre réel t, on peut remplacer l'intégrale curviligne par une intégrale sur un intervalle réel :
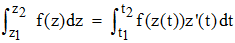
∗∗∗
Un exemple : soit (c) le cercle de centre zo,
de rayon 1. Son équation peut s'écrire z(t) = zo + eit.
Montrer que

L'intégrale d'une fonction non holomorphe présentant des singularités isolées, des pôles en particulier (fonction méromorphe), peut exister. Son calcul utilise le puissant théorème des résidus mis en place par Cauchy.
Intégration par calcul d'un résidu : »
|
Des résultats utiles dans la pratique du calcul d'une intégrale sur un contour |
Lors d'intégrations sur R de fonctions continues, on pourra souvent utiliser avantageusement les résultats suivants (» réf.2) :
1 - Majoration de l'intégrale d'une fonction complexe bornée sur un contour :
On suppose f bornée : il existe M > 0 tel que pour tout z de (c), |f(z)| ≤ M. Avec les notations ci-dessus, on a :
|Sn| ≤ |z1 - zo| × |f(c1| + |z2 - z1| × |f(c2)| + |z3 - z2| × |f(c2)| + ... + |zn - zn-1| × |f(cn)|
Dans cette somme, les |zk - zk-1| représentent la distance entre les points Mk correspondants sur (c). Lorsque n tend vers l'infini, |zk - zk-1|2 = Δxk2 + Δyk2 tendent vers dsk2, carré de l'abscisse curviligne de Mk. Parcourons (c) dans le sens des abscisses positives croissantes et passons à la limite. On peut écrire :

2 - Invariance de l'intégrale sur deux contours imbriqués :
Soit U un domaine simplement connexe de contour (c) et (c') ⊂ U, un second contour d'intérieur simplement connexe U'. Alors, si f est holomorphe dans U \U' (U privé de U'), on a :


Preuve : en appelant A un point de (c) et A' l'image dans (c') d'un point a de (c), on peut construire le contour fermé orienté simplement connexe (c") = arc(AA') + (c') + arc(A'A) + (c) sur lequel l'intégrale de f est nulle selon le théorème de Cauchy-Goursat. En considérant que (c') est parcouru dans le sens positif, on parcourt (c) dans le sens négatif . On a donc :

Mais les intégrales sur les arcs AA' et A'A sont opposées, d'où le résultat.
Cet important résultat permettra de calculer des intégrales en modifiant par un choix adéquat le contour d'intégration.
(c) désignant le demi-cercle de centre O de rayon r situé du demi-plan (xOy), on suppose qu'il existe M et k strictement positifs tels que |f(z)| ≤ M/rk pour tout z de (c), alors :
De manière semblable :
(c) désignant le demi-cercle de centre O de rayon r situé du demi-plan (xOy), on suppose a > 0 et qu'il existe M et k strictement positifs tels que |f(z)| ≤ M/rk pour tout z de (c), alors :

Preuve : en remarquant que sur (c), on a z = reiθ, ce qui permet d'écrire |eiaz| = |eiar(cosθ + isinθ)| = |eiarcosθ × e-arsinθ| = e-arsinθ. En module, l'intégrale étudiée s'écrit alors comme étant inférieure à celle de r × e-arsinθ|f(reiθ)| sur l'intervalle [0,π], donc à celle de :

Le changement de θ en π - θ n'affecte pas l'intégrale, on a donc :

Or, sur l'intervalle [0,π/2], la sinusoïde est concave, donc "au-dessus" de la sécante OP d'équation y = 2x/π. Sur l'intervalle considéré, ce résultat permet d'écrire sinθ ≥ 2θ/π et, par suite e-arsinθ ≤ e-2arθ/π. D'où :


et finalement notre intégrale est majorée en module par :

expression tendant vers 0 lorsque r tend vers l'infini.
Application au calcul de l'intégrale de sin(x)/x sur [0,+∞[ : »
|
Théorème de Cauchy-Goursat : |
Si f est holomorphe sur un domaine simplement connexe D, alors pour tout contour inclus dans D :

Cauchy aurait établi ce résultat dès 1814 dans le cas d'un rectangle inclus dans D et le cas général en 1831 en imposant la continuité de la fonction dérivée de f. Un demi-siècle plus tard (1883), Goursat put se passer de cette hypothèse de continuité, mais sa preuve est plus compliquée (» réf. 2 ou 3). L'application de ce théorème conduit facilement au célèbre théorème de d'Alembert relatif aux zéros des polynômes.
» Morera (théorème réciproque) , Goursat
Formules intégrales de Cauchy (1831) :
f(n) désignant la fonction dérivée n-ème d'une fonction complexe f holomorphe sur un domaine simplement connexe D ainsi que sur son contour (c), on note zo un point intérieur à D. On appelle formules intégrales de Cauchy (ou simplement Intégrales de Cauchy ) les égalités (pour une preuve » réf. 2 ou 3) :
Série de Taylor d'une fonction complexe :
On démontre, au moyen des intégrales de Cauchy ci-dessus, que :
Si f est holomorphe au point zo, alors il existe un disque ouvert D de centre zo sur lequel f est holomorphe, y compris sur sa frontière, et une unique suite (an) de complexes tels que pour tout complexe z de D :
f(z) = f(zo) + (z - zo)f '(zo) + (z - zo)2f '(zo)/2! + ... + (z - zo)nf (n)(zo)/n! + ...
C'est dire que le développement en série entière d'une fonction holomorphe coïncide avec ce que l'on appelle encore dans ce cas complexe la série de Taylor associée à f.
Fonctions méromorphes et séries de Laurent : »
1°) On pose z = x + iy et f(x + iy) = P(x,y) + iQ(x,y). Vérifier que l'on peut alors écrire :

2°) f ' étant continue dans D, utiliser la formule de Green-Riemann afin d'obtenir :

et :

En déduire le résultat cherché en utilisant les conditions de Cauchy pour la dérivabilité de f.
♦ Concernant la seconde intégrale, on remarquera que si l'on entoure zo d'un contour (c') suffisamment petit pour être intérieur à D, l'intégrale en question sur (c) coïncide avec celle sur (c'). Prenons (c') égal au cercle de centre zo de rayon ε :

On peut écrire :

A droite du signe d'égalité, l'holomorphie de f permet d'exprimer
que le premier intégrande est continue sur le domaine limité par (c'), y compris
en zo car il admet la limite
f![]() '(zo)
lorsque z tend vers zo. Soit M son maximum.
Selon le résultat sur la majoration des intégrales de fonctions
bornées, on peut écrire :
'(zo)
lorsque z tend vers zo. Soit M son maximum.
Selon le résultat sur la majoration des intégrales de fonctions
bornées, on peut écrire :

Ce qui montre que la première intégrale du second membre a pour limite 0 si tend ε vers 0. Quant à la seconde, on sait qu'elle vaut 2iπ. Finalement, en faisant tendre ε vers 0, on obtient :

d'où le résultat cherché.
Intégration par calcul d'un résidu : »
♦ Concernant la troisième intégrale, on en admettra ici le résultat. La preuve est présente dans de nombreux manuels et sites. On pourra la vérifier par récurrence en admettant que l'on peut dériver sous le signe d'intégration.
➔ Pour en savoir plus :