Aire sous la parabole

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Aire sous la parabole        ∗∗∗ niveau Terminale S
     Cet exercice utilise la somme des n premiers carrés ainsi que la somme des n premiers cubes d'entiers naturels
      » Nicomaque de Gérase

Par une méthode proche de celle d'Archimède, qui utilisa l'exhaustion, l'objectif est de prouver, par un encadrement élémentaire et un passage à la limite (coïncidant à l'approximation d'une intégrale par la méthode des rectangles), que l'aire bleue ci-dessous, définie par la parabole d'équation :

y = x² sur l'intervalle [-2;2]

est égale aux 4/3 de l'aire du triangle AOB.

Par symétrie, on peut restreindre l'étude à l'intervalle [0;2]. On pose :

f : x → x², x∈[0;2]

et on note S l'aire sous l'arc de parabole (en jaune ci-dessus) restreint à l'intervalle [0;2] que nous subdivisons en n sous-intervalles d'égale amplitude :

0 = x_o < x₁ <x₂ < ... < x_n = 2

1°) En remarquant que f est croissante et en observant les deux graphiques ci-dessous établis pour n = 8 à titre d'illustration (non, non, ce ne sont pas les mêmes...), justifier que l'on :

En déduire :

2°) Somme des n premiers carrés d'entiers naturels

Gauss, alors enfant, a montré que la somme des n premiers entiers naturels est n(n + 1)/2. Nous allons utiliser ce résultat afin d'établir, en exercice ci-dessous la formule donnant la somme des carrés, en évitant un raisonnement par récurrence obligeant à parachuter une formule peu intuitive, à savoir :

On connaît le développement de (a + b)³, cas particulier de la formule du binôme : (a + b)³ = a³ + 3a²b+ 3ab² + b³ :

(1 + 1)³ = 1³ + 3.1².1 + 3.1.1² + 1³(2 + 1)³ = 2³ + 3.2².1 + 3.2.1² + 1³

Compléter maintenant les égalités :

(3 + 1)³ = 3³ + ...
(4 + 1)³ = 4³ + ...
...
(n -1) + 1)³= (n - 1)³ +...
(n + 1)³ = n³ +...

Vérifier par sommation membre à membre, que l'on a l'égalité suivante :

Remplacer la somme des entiers par la formule connue. En déduire la formule annoncée de la somme des carrés.

Somme des n premiers cubes d'entiers naturels

De façon analogue, en utilisant la puissance 4ème du binôme et le résultat précédent :

(1 + 1)⁴ = 1⁴ + 4.1³.1+ 6.1²1² + 4.1.1³+ 1⁴(2 + 1)⁴ = 2⁴ + 4.2³.1+ 6.2²1² + 4.2.1³+ 1^4

...(n + 1)⁴ = n⁴ + 4.n³.1+ 6.n²1² + 4.n.1³+ 1⁴

Par sommation membre à membre, on obtient l'égalité suivante :

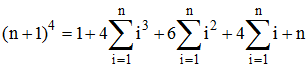
Noter S la somme des cubes. Exprimer 4S en mettant n + 1 en facteur et en remplaçant la somme des carrés ainsi que la somme des entiers par les formules désormais connue.

La somme des cubes des n premiers entiers naturels est ainsi le carré de la somme de ces entiers :

1 + 2³ + ... + n³ = n²(n + 1)²/4 = (1 + 2 + ... + n)²

3°) En utilisant cette formule dans l'encadrement de S établi précédemment, justifier que S = 8/3.

4°) Calculer l'aire du triangle AOB; conclure.

➔ Connaissant le calcul intégral, on vérifie facilement la justesse du calcul :