
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
 Juriste
de formation, diplomate, Gottfried Leibniz est principalement et universellement
reconnu comme l'un des plus éminents philosophes et savants du 17è siècle à l'époque de Louis XIV.
Lors d'un séjour diplomatique à Paris (1672), il rencontre
Christiaan Huygens
qui l'encourage
à étudier les mathématiques. Leibniz ne quittera Paris qu'en 1676. C'est ainsi
qu'il commence à écrire des mémoires relatifs à l'analyse combinatoire imprégnés
des travaux de Pascal et de
Fermat sur le sujet (1673) et les prémisses (1675) de sa
methodus differentialis (Leibniz écrivait en
latin) basée sur la méthode des indivisibles de
Cavalieri.
Son Analysis situs
(1679), annonce
la topologie combinatoire et les
premiers travaux de Euler sur ce qui deviendra
la théorie des graphes.
Juriste
de formation, diplomate, Gottfried Leibniz est principalement et universellement
reconnu comme l'un des plus éminents philosophes et savants du 17è siècle à l'époque de Louis XIV.
Lors d'un séjour diplomatique à Paris (1672), il rencontre
Christiaan Huygens
qui l'encourage
à étudier les mathématiques. Leibniz ne quittera Paris qu'en 1676. C'est ainsi
qu'il commence à écrire des mémoires relatifs à l'analyse combinatoire imprégnés
des travaux de Pascal et de
Fermat sur le sujet (1673) et les prémisses (1675) de sa
methodus differentialis (Leibniz écrivait en
latin) basée sur la méthode des indivisibles de
Cavalieri.
Son Analysis situs
(1679), annonce
la topologie combinatoire et les
premiers travaux de Euler sur ce qui deviendra
la théorie des graphes.
Contrairement à la très grande majorité des mathématiciens, physiciens et astronomes de son époque, Leibniz ne fut pas un enseignant. Il publia la majorité de ses travaux dans la revue Acta eruditorum (Actes des érudits), première revue littéraire et philosophique fondée à Leipzig en 1682 par Othon Mencke (1644-1707), professeur de philosophie dans cette ville, avec la collaboration de Leibniz. C'est dans cette revue qu'il sera l'inventeur, (1684-86) du calcul différentiel et intégral : Nova methodus pro maximis et minimis, itemque Tangentibus.
En Angleterre, Newton qui préparait sa Méthode des fluxions depuis 1669, autre approche du calcul différentiel n'apprécia guère. Ce n'est qu'en 1687 que sa méthode est publiée (en latin) avec ses Principia Mathematica. (puis en anglais en 1736). Une grave polémique naîtra entre les deux Écoles anglaise et allemande, chacune soutenant son champion et accusant l'autre de plagiat ou formulant des critiques plus ou moins justifiées. Les notations de Leibniz, plus pratiques et plus soucieuses d'unité dans le vocable mathématique, devaient finalement l'emporter définitivement (1820) après 90 ans de disputes...
Point de vue de d'Alembert sur la paternité du calcul différentiel : »
Outre ses travaux fondamentaux dans la théorie des fonctions et de leur développement en série ainsi que ses recherches en logique pour un langage symbolique, Leibniz expose des résultats novateurs en géométrie, dans ce qu'il appela Geometria situs (géométrie de situation) pour exprimer que l'on étudie les propriétés des figures mathématiques selon leurs positions relatives dans l'espace indépendamment de leur aspect métrique (mesures, angles).
En savoir un peu plus sur l'Analysis situs de Leibniz : »
A cette époque, mathématique, astronomie, théologie et philosophie sont encore intimement liées et cette revue permit à de grands mathématiciens, comme les Bernoulli, amis de Leibniz, de faire connaître leurs travaux. En France, en 1665, époque de Colbert, naissait le premier journal littéraire, intitulé journal des savants, créé par l'historien François Eudes de Mézeray.
![]() Rappelons
que jusqu'aux années 1960, il était bon de faire ses
humanités : le bon élève, celui qui avait de l'avenir..., était
avant tout littéraire et pratiquait le grec et le latin. Être
savant signifiait avant tout posséder une érudition littéraire et
philosophique. Et se reporter sur les sections dites
modernes (à vocation mathématique) relevait alors presque du péjoratif...
Rappelons
que jusqu'aux années 1960, il était bon de faire ses
humanités : le bon élève, celui qui avait de l'avenir..., était
avant tout littéraire et pratiquait le grec et le latin. Être
savant signifiait avant tout posséder une érudition littéraire et
philosophique. Et se reporter sur les sections dites
modernes (à vocation mathématique) relevait alors presque du péjoratif...
Leibniz inventa une machine à calculer (1685, fabriquée en 1694) et décrivit le principe du calcul binaire (1703) : c'est à dire l'écriture des nombres à l'aide des seuls chiffres, 0 et 1 : système binaire (base 2) qui sera pleinement exploité au 20è siècle pour la construction des calculatrices et des ordinateurs.


Cliquez sur une image pour l'agrandir
Systèmes de numération : » » Pascal , Couffignal
| Le concept de fonction, la notation fonctionnelle : |
 Dans
ses écrits, Leibniz introduit le concept de
fonction
(le terme est de lui en 1692 : en latin
functio = accomplissement, exécution, repris et
clairement défini par Johann
Bernoulli en 1718) et de fonction
dérivée,
à travers celui de
différentielle,
que Newton
appela fluxion.
Dans
ses écrits, Leibniz introduit le concept de
fonction
(le terme est de lui en 1692 : en latin
functio = accomplissement, exécution, repris et
clairement défini par Johann
Bernoulli en 1718) et de fonction
dérivée,
à travers celui de
différentielle,
que Newton
appela fluxion.
Leibniz et Johann Bernoulli utilisèrent des lettres grecques pour désigner des fonctions, comme ξ pour désigner une fonction de x, le ξ grec -prononcer ksi- correspondant à notre x. Johann Bernoulli utilisa aussi φx (phi x). Le nombre x généralement qualifié de quantité variable ou indéterminée, prend le simple nom de variable de la fonction considérée. La notation f(x) fut utilisée par Euler (1734), puis Clairaut. Elle s'imposera avec Lagrange et d'Alembert dans les années 1750. Dès cette époque y désigne généralement le nombre f(x). On a gardé cette écriture simplifiée y dans le vocabulaire des équations différentielles.
Écrit manuellement, la notation
pouvait induire en erreur : par exemple, fx+1 peut se
comprendre fx augmenté
de 1 ou f appliqué à (x + 1) ?
Aujourd'hui, nous écrivons sans
ambiguïté f(x) + 1.
Il n'y a bien évidemment pas que des fonctions d'une seule variable : une écriture comme f(x,y) = x - y désigne une fonction de deux variables. à ce propos, préférer les expressions fonction d'une variable, de deux variables, de plusieurs variables, plutôt que fonction à une variable, à deux variables, à plusieurs variables, tout comme on doit parler du vélo de Paul et non pas du vélo à Paul...
C'est à
Lagrange
que l'on devra le terme de dérivée
et la notation
f![]() 'x puis
f
'x puis
f![]() '(x) pour
exprimer dy/dx,
f
'(x) pour
exprimer dy/dx,
f![]() ''(x) = d2y/dx2
(dérivée seconde = dérivée de la dérivée). On parle de dérivée d'ordre 2. Pour des
dérivées d'ordre supérieur, f
''(x) = d2y/dx2
(dérivée seconde = dérivée de la dérivée). On parle de dérivée d'ordre 2. Pour des
dérivées d'ordre supérieur, f![]() (n)
désigne de façon récurrente la fonction dérivée de f
(n)
désigne de façon récurrente la fonction dérivée de f![]() (n-1) avec
la convention f
(n-1) avec
la convention f![]() (0) = f.
f
(0) = f.
f![]() ' est ainsi
f
' est ainsi
f![]() (1),
f
(1),
f![]() '' = (f
'' = (f![]() ')'
est f
')'
est f![]() (2),
etc.
(2),
etc.
Ce sont encore Leibniz et Johann
Bernoulli qui mirent en place les premières études des fonctions
exponentielles en 1695, année où Johann,
abandonnant la médecine est nommé professeur de mathématiques à Groningen.
En savoir plus sur la notion de fonction : »
La notion de courbe, associée à une fonction,
est rattachée à une vision cinématique comme
chez Neper, Descartes
et Newton
: la continuité reste implicite. Pour ces concepts, indissociables d'une construction
préalable des nombres
réels, il faudra attendre d'Alembert, Lagrange, Euler
et, pour une plus grande rigueur, Cauchy, Riemann, Weierstrass.
Cependant, pour Leibniz, l'absence des nombres réels ne fut pas un obstacle. Ce dernier avait énoncé sa loi de continuité de la Nature, selon laquelle cette dernière ne fait pas de saut : Natura non facit saltum. Le calcul différentiel est une application de ce principe naturel quelque peu mis à mal avec la découverte des quantas dans la mécanique de l'atome.
Lagrange et le sens de variation d'une fonction : »
L'apparition, sans doute prématurée, de l'écriture fonctionnelle en classe de 3ème pose souvent problème d'autant qu'elle est introduite avec des fonctions linéaires et affines qui sont bien mieux assimilées avec les notations simplifiées y = ax et y = ax + b introduites dans le même cours...
Dans le langage courant, dire que y est fonction de x signifie que y peut s'exprimer au moyen d'une expression mathématique faisant intervenir x. Par exemple, le périmètre p d'un carré est fonction de la mesure de son côté c car p = 4c et on peut écrire de façon "plus fonctionnelle" : p(c) = 4c.
L'écriture p(1,25) signifiera le périmètre d'un carré de côté c = 1,25 unités, soit p(1,25) = 5. Le périmètre p d'un rectangle est fonction de sa largeur et de sa longueur; si x et y désignent respectivement ces deux grandeurs, on peut écrire p = 2x + 2y et plus "fonctionnellement" p(x,y) = 2x + 2y.
∗∗∗
Le périmètre d'un carré est le double de celui d'un
rectangle dont la largeur est la moitié de sa longueur L.
Quelle est, en fonction de L, la mesure c du côté de ce carré ?
Rép. : selon l'énoncé,
on peut écrire 4 × c = 2 × (2 × L + 2
x L/2), d'où 4c = 6L et c = 3L/2
➔ Noter que parler d'une fonction f(x) était tout à fait correct avant la "modernisation" des mathématiques (époque Bourbaki, 1939). Depuis, f(x) est l'image de x par la fonction f et on note f : x → f(x) la fonction qui à x associe f(x). Les concepts plus récents d'application, d'application biunivoque (bijection) seront le fait de Dedekind.
|
Le calcul infinitésimal (calcul de l'infiniment petit) également dit différentiel et intégral : |
Les premières ébauches du calcul intégral initiées dès l'antiquité par Eudoxe et Archimède et, plus "récemment", par Cavalieri avec sa méthode des indivisibles n'avaient pour vocation que les calculs d'aires et de volumes. Les calculs différentiel et intégral (dit sommatoire par Leibniz, » infra), permettront de résoudre de subtils problèmes de mécanique non résolus jusqu'alors (comme la célèbre cycloïde et le problème du brachistochrone) en centrant la recherche sur le concept analytique de tangente à une courbe. C'est avec Leibniz et les Bernoulli que naît le calcul des variations.
On doit à Leibniz (1675) :
Le dy pour la différentielle de y
fonction de x (Leibniz parlait alors de
différence). Avec
les notations et le vocabulaire d'aujourd'hui, si f est
dérivable dans un voisinage de x, de dérivée
f![]() ', la différentielle de
f au point x est le nombre :
', la différentielle de
f au point x est le nombre :
df =
f![]() '(x).dx
'(x).dx
Cette formule permet de calculer des valeurs approchées de la forme f(x + h) où h est "petit" devant x en assimilant (cependant faussement) df à son accroissement Δy = f(x + Δx) - f(x) :
Différentielle d'une fonction d'une ou plusieurs variables : » » Barrow
Leibniz précise les différentielles de z = u + v, z = uv et z = u/v en justifiant qu'il est cohérent de négliger les termes de la forme du x dv. Il manipule des "infiniment petits" : on ne passe pas encore à la limite. On ne parle pas non plus de fonction continue.
d'Alembert et la dérivation : » Équations différentielles (généralités) : »
L'écriture dy
:
dx, pour signifier le quotient dy/dx, utilisée en terme de
coefficient directeur (pente)
de la tangente à une courbe
au point M(x,y). Rappelons que Newton
nota  (y
pointé) ce
nombre, aujourd'hui dit dérivé,
qu'il appela fluxion (»
fluxion selon d'Alembert).
Cette notation pointée est encore utilisée en physique dans l'étude d'équations
différentielles, de systèmes dynamiques,
etc.
(y
pointé) ce
nombre, aujourd'hui dit dérivé,
qu'il appela fluxion (»
fluxion selon d'Alembert).
Cette notation pointée est encore utilisée en physique dans l'étude d'équations
différentielles, de systèmes dynamiques,
etc.
Dérivation, différentielle & application linéaire tangente : » Différence finies : »
La notation ds2 = dx2 + dy2 , pour la longueur d'un arc infinitésimal.
Calcul de la longueur d'un arc de courbe (rectification) : »
Le signe ∫ pour l'intégrale (c'est un s pour sommation du latin summa ) : Leibniz parlait de calculus summatorius (calcul sommatoire) alors que Johann Bernoulli, qui préférait calculus integralis, utilisa un I (i majuscule). A la même époque, Leibniz utilisait aussi l'abréviation omn. pour omnia (signifiant tout, toutes choses) mais le signe somme ∫, plus pratique fut très vite adopté.
» Les Bernoulli préférèrent en effet calcul intégral plutôt que sommatoire. Leur appellation l'emporta. Les deux vocables expriment la même idée de faire la somme de toutes les différences très petites qui, ainsi fusionnées, produisent une nouvelle grandeur (longueur d'un arc, aire, volume, travail d'une force, moment d'inertie, etc.).
L'intégrale de Riemann et le calcul de ses sommes, retirée des programmes de Terminales depuis une vingtaine d'années donnaient un sens tant au vocabulaire qu'à l'objet mathématique représenté par l'intégrale.
Liés à ces calculs des sommes de séries numériques, on doit aussi à Leibniz les principaux résultats relatifs à la rectification des courbes (calcul de la longueur d'un arc de courbe définie par une équation), aux calculs d'aires et de volumes en énonçant le théorème fondamental liant l'aire sous la courbe aux primitives de la fonction et en considérant le processus de "sommation" comme réciproque de la "différentiation"; c'est encore à lui que l'on doit la formulation "moderne" du calcul d'un volume de révolution utilisée implicitement par ses illustres prédécesseurs Archimède (méthode d'exhaustion) et Cavalieri (méthode des indivisibles), à savoir :
V = π∫[x1,x2] y2dx Cas du volume de la sphère : »
Les équations différentielles et aux dérivées partielles :
Le concept de différentielle
évoqué ci-dessus permit à Leibniz de résoudre des
équations fonctionnelles (l'inconnue est une fonction) où apparaissent tant la
variable x que la fonction y = f(x) et/ou au moins une de ses dérivées y' =
f![]() '(x), y" =
f
'(x), y" =
f![]() ''(x), fonction
dérivée de la fonction dérivée f
''(x), fonction
dérivée de la fonction dérivée f![]() ',
etc. : on parle d'équations différentielles.
On précise du 1er ordre si y' seule intervient, du second ordre si y"
intervient, etc.
',
etc. : on parle d'équations différentielles.
On précise du 1er ordre si y' seule intervient, du second ordre si y"
intervient, etc.
Le cas le plus élémentaire est de la forme A(x) = y'B(y) : on parle de séparation des variables. Au moyen des différentielles, y' peut s'écrire dy/dx et une telle équation prend la forme A(x)dx = B(y)dy, ce qui justifie pleinement le nom d'équation différentielle. Au moyen d'une simple quadrature (en intégrant les deux membres) :
∫A(x)dx = ∫B(y)dy + C,
on obtient une expression de la forme F(x,y) = 0 caractérisant la relation entre x et y, équation d'une courbe plane prenant dans ce contexte le nom de courbe intégrale.
Exemple : l'équation xyy' = 1 se résout simplement en l'écrivant sous la forme yy' = 1/x, car x est non nul. On a ainsi séparé les variables. Par suite xyy' = 1 ⇔ 2yy' = 2 × 1/x et il suit que y2 = 2ln |x| + k = ln x2 + k, ln désignant le logarithme népérien et k, une constante quelconque.
Le cas général peut s'avérer difficile. Certaine équations ne peuvent être résolues par quadrature (intégration par recherche de primitives), on a alors recours à un développement en série entière de type Σanxn conduisant à la recherche des coefficients an. Dans le cas d'une fonction f de plusieurs variables, une équation faisant intervenir une ou plusieurs de ses dérivées par rapport à une ou plusieurs de ses variables est qualifiée d'équation aux dérivées partielles. Le sujet est encore beaucoup plus difficile.
Équations différentielles, cas classiques : » Équations aux dérivées partielles, généralités : »
|
Règles de Leibniz, dite de dérivation et d'intégration sous le signe somme d'une fonction de deux variables : |
♦ J désignant un intervalle de R et f est une fonction numérique (ou plus généralement à valeurs dans un espace vectoriel normé) continue des deux variables x∈J et t∈[a,b], alors la fonction F définie par :

est continue sur J et si f est continûment dérivable sur J par rapport à x, alors F est dérivable sur J et :
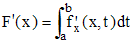
∗∗∗
Étude de la fonction F(x) =
∫[o,π]cos(x
sint)dt : cliquez-moi...
Cas d'une seule variable x apparaissant dans une borne d'intégration : » Valeur principale de Cauchy : »
♦ La règle d'intégration sous le signe somme :
Cette règle exprime, sous la seule condition de continuité de f en x et en t que si [u,v] est un intervalle de J, alors :

Le cas des intégrales généralisées (une borne au moins de l'intervalle d'intégration de f(x,t) est infini) est plus délicat :
Cas des intégrales généralisées, exemples : »
| Critère de Leibniz pour les séries alternées : |
Ce critère ne s'applique qu'aux séries alternées : si | un | tend vers 0 en décroissant, alors la série Σun converge et | Σun+k | avec k ≥ 1 (valeur absolue du reste), est inférieur à un+1.
Ce résultat fondamental permet de prouver la convergence d'un grand nombre de développements en série usuels comme ceux des fonctions sin x, cos x, tan x, ln(1 + x), etc. Ce critère prouve, par exemple, que la série harmonique alternée (également dite semi-harmonique) :
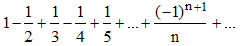
est convergente : sa somme est ln 2, logarithme népérien de 2.
Étude de la érie harmonique : » Série de Mercator : » Un calcul de π : »
∗∗∗ un petit exo à propos de la série harmonique
! Le critère de Leibniz ne peut pas s'appliquer à l'étude de la série alternée de Grandi 1 - 1 + 1 - 1 + 1 - 1 +.... dont la somme n'est ni 0, ni 1, ni 1/2... (suivant l'ordre de sommation des termes). Cette série doit être déclarée divergente. Tout dépend évidemment de ce que l'on entend par série convergente. Depuis Cauchy, le terme général doit tendre vers 0, ce qui n'est pas le cas ici. Même chez Euler, le problème n'était pas clair (il manipule avec bonheur diverses séries sans toujours se soucier de leur convergence). Il faudra attendre Dirichlet et Cauchy pour une définition rigoureuse de la convergence.
Quoi qu'il en soit, il est tout à fait illicite de changer l'ordre des termes d'une série si elle n'est pas absolument convergente (c'est à dire si la série de terme général |un| diverge). Dans le cas de la série harmonique alternée ci-dessus, on peut écrire :
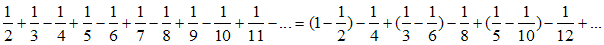
en regroupant chaque terme positif avec le terme négatif suivant. On obtient alors la série :
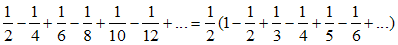
qui converge donc vers ½ln 2 = ln√2 ! Un autre arrangement plus subtil rend cette suite divergente.
Séries séries de fonctions, convergences simple, uniforme et normale : »
| Premiers développements en série des fonctions élémentaires : |
Leibniz établit (1673), parallèlement aux travaux de Newton, le développement en série des fonctions trigonométriques usuelles par des méthodes différentielles (recherche d'un développement en série d'une fonction à partir d'une équation différentielle qu'elle satisfait). Il obtint ainsi par exemple :
sin x = x - x3/3! + x5/5! - x7/7! + ... + (-1)nx2n+1/(2n+1)!
A propos de la fonction sinus, Leibniz, et encore son concurrent Newton, étudieront ses propriétés et sa courbe représentative : la sinusoïde, appelée ainsi ultérieurement dans l'Encyclopédie de d'Alembert (1751), fut au préalable décrite par Roberval.
La célèbre (dans le monde mathématique...) somme :
fut aussi établie par Leibniz. Également attribuée à Gregory, elle est conséquence du développement de atn x (atn = arc tangente) lorsque x = 1.
Formule de Taylor et développement limité :
»
Développements en série usuels : »
| Formules de Leibniz, Fonction scalaire de Leibniz, Fonction vectorielle de Leibniz : |
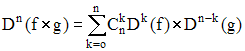
Pascal et les combinaisons : »
Si G désigne le barycentre (» barycentre) d'un système de points pondérés (Ai,ai) :
![]()
∗∗∗
Si Σai = 0, le barycentre des Ai est
inexistant. Montrer que le vecteur f(M) est constant (indépendant de M).
![]()
Si G désigne le barycentre (» barycentre) d'un système de points pondérés (Ai,ai) :
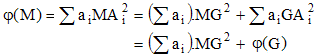 (relation de Leibniz)
(relation de Leibniz)
∗∗∗
a) On considère un triangle ABC et M un point intérieur à
M. Montrer que MA2 + MB2 + MC2 est minimale
lorsque M = G.
b) Si Σai = 0, le barycentre des Ai
est inexistant. Montrer que pour tout point K :
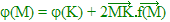
» Archimède , Möbius , König » Coordonnées barycentriques
➔ Noter que l'appellation "vectorielle" pour la fonction f est impropre car la notion de vecteur n'est pas encore dégagée. Il faudra attendre la fin du 18è siècle avec Stewart, Argand, puis Bellavitis, Chasles, Möbius et, pour une formalisation (analyse vectorielle ), Hamilton, Gibbs et Grassmann.
La notion de vecteur : »
| Notation de Leibniz pour la multiplication et la division : |
Plus anecdotique mais pratique, voire fondamentale dans l'écriture mathématique, est la notation implicite de la multiplication que Leibniz proposa. Dans une lettre à Johann Bernoulli, il estimait, à juste titre, que la notation a ×b d'Oughtred prêtait à confusion avec le x de l'algèbre : c'est pourquoi il utilisa a.b puis ab (notation implicite) au lieu de a x b, ainsi que a : b pour exprimer le quotient de a par b, parfois plus commode que la notation fractionnaire usuelle déjà utilisée depuis fort longtemps :
| Leibniz philosophe, logicien et précurseur de la topologie : |
A noter les travaux infructueux de Leibniz, sans doute trop novateurs et, par
là, insuffisamment entendus, dans sa quête d'un
langage mathématique universel (logique symbolique). Il
écrivait en 1667 au Père Berthet (Leibniz,
Oeuvres choisies, Ed. Garnier) :
(...) Je tiens pour assuré qu'on ne saurait presque obliger davantage le genre humain qu'en établissant une caractéristique telle que je la conçois. Car elle donnerait une écriture ou, si vous voulez, une langue universelle qui s'entendrait de tous les peuples.
Cette langue s'apprendrait tout entière (au moins pour le plus nécessaire) en peu de jours et ne se saurait oublier pourvu qu'on en retint quelque peu de chose. Mais le principal serait qu'elle nous donnerait un filum meditandi, c'est à dire une méthode grossière et sensible, mais assurée de découvrir des vérités et résoudre des questions ex datis.
(...) et comme l'esprit se perd et se confond lorsqu'il y a un grand nombre de circonstances à examiner ou des conséquences à poursuivre (...), on se délivrerait par ce moyen des inquiétudes qui agitent l'esprit çà et là et qui le font flotter entre la crainte et l'espérance, en sorte que souvent, au bout de la délibération, on est aussi avancé ou moins qu'auparavant.
Durant cette même période, dans des correspondances avec Huygens et des essais (1676-1679) qu'il qualifia d'Analysis situs, Leibniz cherche à schématiser et résoudre des problèmes combinatoires dans un contexte universel (arithmétique, géométrique et logique) : il apparaît ainsi comme un précurseur de la théorie des graphes et de la topologie combinatoire.
» Analysis situs : du grec et du latin savant analysis = analyse, étude et situs = situation, position (au sens des cas et configurations à envisager). Poincaré utilisera encore cette dénomination malgré le nouveau terme de topologie créé par Listing en 1836.
Euler et la théorie des graphes : » Notions élémentaires de théorie des graphes (niveau Ter ES) : »
Ce sera De Morgan et Boole, un siècle et demi plus tard, qui exauceront le vœu de Leibniz, suivis par Cantor, Peano, Frege et bien d'autres avec la mise en place du langage des ensembles et du calcul des propositions dans cette période passionnante mais tourmentée pour les mathématiques que l'on a appelé la crise des fondements, avec la découverte des contractions apparues dans la théorie des ensembles.
