ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

EULER Leonhard Paul, suisse, 1707-1783     » Fonction Γ | Formules d'Euler | Cte d'Euler | Identité d'Euler (produit eulérien) | Nombres d'Euler | Cercle des 9 points | Graphes | Calcul des variations

Né à Bâle d'un père pasteur, Leonhard, esprit brillant étudia les lettres, la théologie et la médecine et semblait, à 17 ans, voué aux ordres religieux. Les Bernoulli étaient des amis de la famille et il fut l'élève de Jean Bernoulli qui persuada Euler père de laisser son fils s'orienter vers les mathématiques. A 18 ans, il se faisait connaître à l'Académie des sciences de Paris par divers mémoires comme ceux sur la théorie des marées et la propagation du son.

Introduit par les Bernoulli, il s'installa à Saint-Pétersbourg (1727), alors capitale de l'empire russe, auprès de Pierre Ier le Grand et remplaça Daniel Bernoulli (1733) à l'Académie des sciences pour la physique et les mathématiques. Dès 1735, à la suite d'une congestion cérébrale, Euler perd l'œil droit.

Appelé à Berlin (1741) par Frédéric II, roi de Prusse, il y présida l'Académie des sciences jusqu'en 1766 (c'est Lagrange qui lui succédera). Il fut nommé membre associé de l'Académie des sciences de Paris (1755). Vers la fin de sa vie, alors aveugle, il revint à Saint-Pétersbourg invité par Catherine II, ce qui ne l'empêcha pas de publier ses Éléments d'algèbre (1768) et trois plus tard, son volumineux traité sur la dioptrique (1769-71). Il est sans doute un des plus grands mathématiciens de tous les temps.

 ➔   Trois fils de Euler furent aussi des personnalités renommées :

• Jean-Albert (1734-1800) : né à Saint-Pétersbourg, mathématicien et brillant astronome, il dirigea, dès l'âge de 20 ans, l'observatoire de Berlin. Conseiller d'État à Saint-Pétersbourg, il poursuivit des recherches en astronomie et remporta avec Clairaut le prix de l'Académie des sciences de Russie Sur la théorie des comètes (1763), puis, avec son père celui de l'Académie des sciences de Paris Sur la théorie de la Lune (1770).

• Charles (1740-1790) : né à Saint-Pétersbourg, médecin et astronome, prit la nationalité russe. Professeur de médecine à l'académie des sciences de Saint-Pétersbourg. Il remporta le prix de l'Académie des sciences de Paris Sur la marche des planètes (1760), bien qu'un soupçon sur une aide paternelle ait été évoquée...

• Christophe (1743-1812), né à Berlin, ingénieur militaire auprès du roi Frédéric II de Prusse, puis de l'impératrice Catherine II de Russie.

L'œuvre de Leonhard Euler est considérable. Il intervint dans les trois domaines fondamentaux de la science de son époque : l'astronomie (orbites planétaires, trajectoires des comètes), les sciences physiques (champs magnétiques, hydrodynamique, optique, nature ondulatoire de la lumière, mécanique des solides...), et les mathématiques, dans toutes ses branches, de l'arithmétique à la géométrie différentielle en passant par :

• l'algèbre et l'analyse numérique et fonctionnelle;

• le calcul des variations;

• la géométrie élémentaire et ses transformations, comme l'affinité : » Affinité géométrique

• les courbes et les surfaces algébriques;

• le calcul des probabilités;

• les premiers aspects de ce qui deviendra la théorie des graphes;

• la topologie.

Dans cet immense traité, Euler procède à une vaste synthèse des connaissances en matière d'Analyse qu'il construit au moyen du concept de fonction sans le soutien géométrique ou mécanique. Les fonctions trigonométriques, logarithmes et exponentielles s'avèrent étroitement liées :

• Si y = a^x, fonction exponentielle de base a, a > 0, a ≠ 1 , alors x est le logarithme de y dans la base a :

• C'est à Euler que l'on doit l'écriture ci-dessous afin de définir le logarithme hyperbolique, dit de nos jours népérien, forgé sur le nom de John Napier (Neper), autrefois noté Log et noté aujourd'hui ln, pour tout x > 0 :

 ∗∗∗ 
Justifier que :  a^{x + x'} = a^xa^x' et (a^x)^x' = a^xx' puis résoudre le système suivant sans passer par les log : 2^x-1 = 8^y , 3^x-10 = 9^y-1  ☼

• La notation π, le p grec, première lettre du mot grec périmêtron signifiant contour, périmètre, qu'avait déjà utilisée Oughtred (dès 1657) et Jones (1706).

Archimède et le Calcul de π : »              Autres Calculs de π dans ChronoMath : » 

• La notation e (dès 1727, il n'avait que 20 ans!) pour le fameux nombre dont le logarithme népérien est 1 (ln e = 1), souvent appelé nombre d'Euler : e comme exponentielle mais aussi comme Euler !

• La notation e^x pour la fonction exponentielle, osé pour l'époque puisque le nombre e n'est pas rationnel, ce que prouva Euler en 1737 dans un opuscule sur les fractions continues : De Fractionibus Continuis Dissertatio.

e^x = 1 + x + x²/2! + x³/3! + ... + xⁿ/n! + ...

Pour x = 1, on obtient  e = 2,7182818284590452353...

• La notation i pour la "racine carrée" de -1 (1777), plus rigoureusement pour le nombre complexe dont le carré est - 1; pourtant ancrée ultérieurement par Gauss, cette notation aura cependant beaucoup de mal à s'imposer, la notation √-1 sera souvent utilisée en fait jusqu'au 20è siècle !
  
   ➔  Il est vrai que la notation i est parfois ambiguë : en électricité, elle génère un conflit avec l'intensité i d'un courant, raison pour laquelle les physiciens utilisent j. Mais j est réservé en mathématiques à une des trois racines cubiques complexes de l'unité, à savoir (-1 + i√3)/2. Les deux autres sont j² = j et 1 lui-même.

»  Argand              Racines n-èmes d'un nombre complexe : »

• La notation Σ (Sigma, S majuscule grec) pour la sommation (1755), deux écritures généralement utilisées :

     Propriétés fondamentales de cet opérateur :   

» En effet, on doit sommer pour toutes les valeurs possibles de i et j. L'addition étant commutative et associative, on peut décider de fixer i = 1, j variant de 1 à m, puis i =2, j variant de 1 à m, etc. Ce qui fournit a1( b1 + b2 ... + bm) + a2( b1 + b2 ... + bm) + ...
Et on obtient finalement le résultat indiqué.

♦ Plus généralement, avec trois séries de nombres (ou plus), on a (sans indiquer ici les limites des index)  :

» Ne pas indiquer les limites des index signifie que la ou les somme(s) sont effectuée(s) pour toutes les valeurs de i, j et k possibles suivant le contexte.

♦ Cas d'indices doubles comme dans le cas d'un tableau matriciel :

♦ On a aussi la généralisation des identités remarquables :

∗∗∗  Sommes d'Euler :
Prouver que si la suite (u_n) converge, alors il en est  de même de la suite (v_n) définie par :

Indications : on s'inspirera de la méthode employée pour prouver la convergence de la somme de Cesaro.

♦  1 - Ayant établi sa célèbre formule réalisant le lien entre la trigonométrie, l'exponentielle et l'analyse complexe :

♦  4 - Soit x → f(x,y) une fonction numérique de deux variables réelles, homogène de degré α admettant sur un ouvert U de R² des dérivées partielles continues. Alors pour tout (x,y) de U :

      (4)

• Par exemple, f(x,y) = 2x³y + y⁴ est homogène de degré 4 : ∂f/∂x = 6x²y et ∂f/∂y = 2x³ + 4y³ et x∂f/∂x + y∂f/∂y = 6x³y + (2x³y + 4y⁴) = 4f(x,y).

Preuve : f étant homogène de degré α, on a, par définition : f(tx, ty) = t^αf(x, y). En différentiant par rapport à t, on obtient le résultat annoncé pour t = 1.

Lorsque f admet des dérivées partielles continues jusqu'au rang n, la formule se généralise au rang n (» notation opérateur) :

La formule (4) se généralise à n variables. Pour 3 variables, on écrirait, avec des notations simplifiées :

xf'_x + yf'_y + zf'_z = αf

Cette formule intervient profitablement dans l'étude des courbes algébriques d'équation implicite f(x,y) = 0 en rendant cette équation homogène au moyen d'une variable z d'homogénéité permettant de plonger la courbe dans le plan projectif.

♦  Autres curiosité numériques : vérifier que e^π - π est "presque" entier; Voyez aussi Ramanujan et le nombre e^π√163.

Toujours dans son Introductio, Euler établit l'existence d'une constante qui deviendra célèbre et portera son nom :

où ln désigne le logarithme népérien. La série 1 + 1/2 + 1/3 +... +1/n + ... est la non moins célèbre série harmonique divergente.

Divergence de la série harmonique, étude et calcul approché de la constante d'Euler ... : »

La nature de C (généralement notée γ, gamma minuscule grec : g), algébrique, irrationnelle, voire transcendante, est un problème ouvert. On en connaît aujourd'hui quelques 20 000 décimales. Euler calcula les seize premières :

γ = 0,5772156649015328...

 ➔  Rappelons que c'est parfois le nombre e, base des logarithmes népériens qui est appelé constante d'Euler. Quant à la constante C, alias γ, elle est souvent appelé constante d'Euler-Mascheroni :

On peut écrire :

Σ _{p ≤ x + k} 1/p - Σ _{p ≤ x} 1/p  ~  ln(ln(x + k)) - ln(lnx) ≃ k × (ln o ln)'(x) = k/(xlnx)     (1)

De plus, compte tenu de notre hypothèse k << x, en assimilant à x tout entier premier p de l'intervalle [x, x + k], on obtient :

Σ _{p ≤ x + k} 1/p - Σ _{p ≤ x} 1/p =  Σ _{x+1 ≤ p ≤ x+k} 1/p ≃ 1/x × (π(x + k) - π(x))     (2)

En identifiant (1) et (2), il vient :

Ce résultat s'interprète comme la densité des nombres premiers sur l'intervalle [x, x + k]. Vu que k est très petit devant x, on peut aussi l'interpréter comme un taux d'accroissement de x → π(x) sur [x, x + k], x ≥ 2, et écrire Δπ/Δx ≃ dπ/dx ≃ 1/lnx, ce qui conduit à :

Il s'agit bien du théorème des nombres premiers.

Fondateur de ce qu'on appelle aujourd'hui l'analyse fonctionnelle (appellation due à Paul Lévy), Euler publia de nombreux traités, précisera la notion de fonction et adoptera la notation f(x), également utilisée par Clairaut, pour désigner l'image par une fonction f d'un nombre x, plus adaptée que celle de Jean Bernoulli qui utilisait la notation f_x.

Prolongeant les travaux des Bernoulli, Euler affine la notion de fonction dérivée, crée, avec Daniel Bernoulli, parallèlement aux travaux de Clairaut et Fontaine en France, la notion d'équation aux dérivées partielles (1734) et développe le calcul des variations (Calculi Variationum, dès 1744) : recherche d'extremums sur des courbes ou des surfaces, une des branches les plus fécondes de l'analyse. On pourra étudier en particulier sur ce site le problème de Didon et le brachistochrone.

Équation d'Euler-Lagrange, formule de Beltrami : »              La notion de surface minimale : »

équation intervenant dans des problèmes oscillatoires. Pour la forme non homogène : ay" + by' + cy = f(x), Laplace inventera la méthode de la variation de la constante afin d'exhiber une solution particulière.

Oscillation d'un ressort, type ay" + by' + cy = 0 : »

Équation d'Euler (ou d'Euler-Cauchy):    

Il s'agit, pour x > 0, de l'équation différentielle linéaire homogène du second ordre :

ax²y" + bxy' + cy = 0

Euler ramène cette équation à des coefficients constants en posant t = lnx (logarithme népérien de x). On peut écrire :

• y' = dy/dx = dy/dt × dt/dx = dy/dt × 1/x

• y" = d²y/dx² = d/dx[dy/dx] = d/dx[dy/dt × 1/x] = d/dx[dy/dt] × 1/x + dy/dt × (-1/x²)
      = d/dt[dy/dx] × 1/x - dy/dt × (1/x²) = d/dt[dy/dt × 1/x] × 1/x - dy/dt × (1/x²) = 1/x² × [d²y/dt² - dy/dt]

En remplaçant dans l'équation d'Euler, on obtient l'équation différentielle linéaire homogène à coefficients constants :

ad²y/dt² + (b - a)dy/dt + cy = 0 , x = e^t

Selon le discriminant Δ de l'équation caractéristique, laquelle est ici ar² + (b - a)r + c = 0, les solutions de cette équation sont de la forme :

• Δ > 0 : y = c₁e^rt + c₂e^r't = c₁x^r + c₂x^r';

• Δ = 0 : y = e^rt(c₁t + c₂) = x^r(c₁lnx + c₂)

• Δ < 0 : deux solutions complexes conjuguées r = u ± iv; y = e^ut(c₁cosvt + c₂sinvt) = x^u[c₁cos(v×lnx) + c₂sin(v×lnx)]

∗∗∗
Résoudre l'équation différentielle d'Euler x²y" + xy' + y = 0, y(1) = 0, y'(1) = 1 ☼

♦ Résolution approchée des équations différentielles :    

On doit à Euler une méthode de résolution approchée des équations différentielles, dite des différences finies  par discrétisation inspirée des idées de Newton sur ce sujet : on recherche la solution y = f(x) sous la forme d'un nuage de point M_i(x_i,y_i) permettant d'obtenir une approche fiable de la courbe intégrale (représentative de la solution fonctionnelle exacte).

Résolution approchée de y' = φ(x,y) et y" = φ(x,y,y') : »            » Newton , Runge

La difficile étude des surfaces est entreprise par Euler grâce à l'apport du calcul différentiel et intégral. Au 19è siècle Gauss et Riemann (tout particulièrement) se pencheront sur cette difficile théorie.

En 1755, Euler publie un traité de calcul différentiel et intégral (complété en 1768 : Institutiones calculi integralis) où l'on y rencontre les fonctions (ou intégrales) dites aujourd'hui eulériennes dont la plus connue, voire célèbre : la fonction Γ (Gamma), ainsi nommée ultérieurement par Legendre. Dite intégrale eulérienne de seconde espèce, elle est définie pour tout nombre x > 0 par l'intégrale généralisée convergente :

Moins célèbre, mais pratique pour l'intégration de certaines fonctions rationnelles, est la fonction β (appellation encore due à Legendre) aussi appelée intégrale eulérienne de première espèce. Pour tout x > 0 et y > 0, elle est définie pas  :

       (β1)

Le changement de variable u = t/(1 - t) conduit à intégrer de 0 à +∞, on obtient :

       (β2)

Euler a montré cette belle formule :

        (β3)

Lorsque x + y = 1, on a Γ(x + y) = Γ(1) = 1 (intégrale sur R⁺ de t →e^-t). En posant traditionnellement x = p, Le calcul de (β2) dans ce cas particulier conduit à la formule des compléments (» preuve en réf. 6c) :

En savoir plus sur la fonction Γ, cas réel et complexe : »               Fonctions Γ de Euler et ζ de Riemann : »

 ➔  Si l'intégrale est calculée non plus sur [0;1] mais sur un intervalle [0;x] avec 0 < x < 1, on parle de fonction β incomplète, notée β_x. Pour en savoir plus sur les intégrales eulériennes et les fonctions elliptiques, on pourra consulter en particulier le mémoire de Legendre (1825) en libre accès sur Google Livres (» réf.6a) et le cours de mathématiques de Jean Bass (»réf.6b).

• En 1732, Euler prouva la non primarité (ou primalité en franglais), en général, des nombres de Fermat, à savoir les nombres entiers naturels de la forme :

F_p=

liés à ceux de Mersenne (forme 2ⁿ - 1) en montrant que F₅ = 2³² + 1 = 4 294 967 297 est divisible par 641.

• En 1738, s'attaquant au fameux grand théorème de Fermat, il le prouva pour les cas n = 4 en recourant aux nombres complexes.

∗∗∗ 
Euler exhiba (1772) le polynôme x² + x + 41 qui, pour x variant de 0 à 39, ne fournit que des nombres premiers.
A vérifier à la main ou sur tableur ! Étudier aussi (encore proposés par Euler) : x² + x + 17 et 2x² + 29

Moins rigolo :
Prouver qu'un polynôme à coefficients entiers ne peut fournir indéfiniment des nombres premiers pour des valeurs entières.
Indications : soit x_o tel que P(x_o) = p premier. Justifier que P(x_o + px) ≡ P(x_o) [p].
On en déduit que P(x_o + px) est divisible par p quel que soit x. Conclure.        » congruences

Reprenant un célèbre problème arithmétique de Pythagore, présent dans les Éléments d'Euclide, Euler étudie les nombres parfaits , c'est à dire égaux à la somme de leurs diviseurs propres, comme 6, 28, 496, ... (un diviseur propre d'un nombre entier est un diviseur de ce nombre autre que lui-même).

Euler conjectura et prouva le résultat suivant :

Un entier pair est parfait si et seulement si il est de la forme 2^n-1(2ⁿ - 1) et 2ⁿ - 1 est premier

L'entier 8128 = 2⁶(2⁷ - 1) est ainsi le quatrième nombre parfait pair (trouvé par Nicomaque), le cinquième est 33550336 avec n = 13. Rappelons que l'existence de nombres parfaits impairs est un problème ouvert.

♦ Une conjecture de Euler (1760) :    

Il existe une infinité d'entiers premiers de la forme 4n² + 1

» Landau

♦ Fonction indicatrice d'Euler ou fonction "totient" :    

Il s'agit de l'application, traditionnellement notée φ, dite également  fonction totient qui à tout entier naturel n non nul associe le nombre d'entiers naturels inférieurs à n et premiers avec n :

φ(n) = Card {k, k∈N, 1 ≤ k ≤ n - 1, pgcd(k,n) = 1}

 i  En anglais, on parle de totient function, du latin totiens = tant de fois, proche de quotiens = combien de fois, mais d'usage interrogatif, qui a donné quotient en français et en anglais : chercher le quotient de n par p c'est chercher combien de fois "il y a p dans n".

• φ(1) = φ(2) = 1, φ(3) = φ(4) = 2, ..., φ(20) = Card {1 , 3 , 7 , 9 , 11 , 13 , 17 , 19 } = 8

• Si n est un entier naturel non premier pour lequel φ(n) divise n - 1, alors n est un nombre de Carmichael.

  Étude de la fonction φ : »            Nombres de Carmichael : »            »  Dirichlet , Bombieri   

L'identité d'Euler également appelée produit eulérien (1750) et la naissance des fonctions ζ :    

Si s désigne un réel et s > 1, la série de terme général 1/n^s est convergente. Par des considérations relativement simples, Euler la transforme en un produit infini :

          »  preuve élémentaire

où P désigne l'ensemble infini des nombres premiers : P = {2, 3, 5, 7, 11, 13, 17, 19 ...}.

Cette identité devait amener Riemann à définir et étudier les fonctions ζ (lire zêta), sommes des séries ci-dessus élargies au champ complexe afin d'étudier la distribution des nombres premiers.

Problème de Bâle (Balsen problem) :   

En 1644, le mathématicien italien Pietro Mengoli avait proposé comme un défi aux mathématiciens européens la recherche de la somme de la série de terme général 1/n² :

Les Bernoulli, en particulier, s'emparèrent sans succès du problème. Euler, alors résidant à Bâle, obtint la somme π²/6 en établissant un produit infini convergeant vers sin(x) et en l'identifiant au développement en série de cette fonction (» réf. 11) :

En 1743, il présenta un calcul plus rigoureux basé sur le développement en série de la fonction Arcsinus et l'équation différentielle du second ordre

(1 - x²)y'' - xy' - 1 = 0 (» réf. 11).

 i  Pietro Mengoli (1626-1686) : natif de Bologne, il s'adonne au droit et à la philosophie avant d'entamer des études de mathématiques auprès de Cavalieri découvrant ainsi les premières ébauches du calcul infinitésimal (méthodes des indivisibles), la géométrie de Descartes et l'algèbre de Viète dont il s'inspirera. Les années 1650-1660 seront les plus productives. Succédant à Cavalieri à l'université de Bologne en 1648, il publiera de nombreux articles et traités (algèbre, analyse, mécanique) dont une une compilation de ses recherches sur les séries (Series lectionum, 1654) où il prouve en particulier la divergence de la série harmonique (avant Jean Bernoulli) et la convergence des séries de terme général 1/(n(n+p), p entier non nul, le cas p = 0 restant problématique. Dans les années  1660,  Mengoli s'oriente vers la religion. Ordonné prêtre, il conserva des postes d'enseignement des mathématiques et de mécanique à Bologne (source : réf.15).

Riemann et les fonctions ζ : »           »  Tchebychev

• Euler établit (1736) un lien entre les nombres de Bernoulli et les fonctions ζ  en montrant que :

Calcul de ζ(4) = π⁴/90 : »

• Par ailleurs, d'après un calcul de Cesaro, l'inverse de ce résultat 6/π², apparaît comme étant la probabilité de choisir au hasard deux nombres entiers naturels premiers entre eux !

A noter cette belle formule d'Euler, dont celle de Wallis est un cas particulier pour x = 1/2 :

Polynômes et nombres d'Euler :

Dans l'étude de développements en série, Euler fait état d'une famille de polynômes x → E_n(x), de degré n, de fonction dérivée E'_n, vérifiant la formule de récurrence :

On a ainsi :

• E_o(x) = 1;

• E₁(x) = x - 1/2;

• E₂(x) = x² - x;

• E₃(x) = x³ - 3x²/2 + 1/4;

• E₄(x) = x⁴ - 2x³ + x;

Nombres d'Euler et nombres ZigZag : »          Nombres de Bernoulli : »

En 1770, Euler publia en allemand (le latin est de plus en plus révolu dans les publications scientifiques) une Introduction complète à l'algèbre (Vollständige Einleitung zur Algebra) où l'on peut considérer que, malgré quelques rebelles, tout sera dit quant aux nombres négatifs et à leur statut de véritable nombre, statut conforté et définitivement entériné avec Gauss (le qualificatif semble apparaître pour la première fois chez Jean de Beaugrand en 1638).

» Chuquet , Stifel , Descartes

De même, les nombres imaginaires (le qualificatif complexe nous vient de Gauss avec la forme a + bi), sont définis et leurs propriétés étudiées.

Euler concevait déjà la notion de nombre transcendant, voire de fonction transcendante, que l'on ne peut obtenir qu'au moyen de séries convergentes ou par le biais de fractions continues comme π, e, ln 2 et plus généralement e^x, sin x, ln x,...

Cependant, R n'étant pas encore construit, les notions de limite, de différentielle et de convergence restent encore approximatives. Le concept de continuité n'est pas encore exhibé ni, a fortiori, celui de continuité uniforme pouvant assurer, dans le cas d'une série convergente de fonctions, la continuité de la somme. Ces préoccupations apparaîtront tout particulièrement dès le début du 19e siècle avec Bolzano, Cauchy, Abel, puis Riemann et Weierstrass.

Le développement du calcul différentiel et intégral répond à la volonté de résoudre efficacement les grands problèmes scientifiques : l'aube du siècle des lumières est celle de la technologie (mécanique, hydraulique, production d'énergie : vapeur, électricité). Il s'agit de comprendre les lois de la nature, du mouvement (vitesse, accélération, extremums).  

Relations :  

1a/  Pour tous points A, B , C et M dans le plan ou l'espace, on a la relation, le point (.) désignant le produit scalaire :

MA.BC + MB.CA + MC.AB = 0

La preuve de ce résultat est très simple en utilisant la formule de Chasles.

1b/  Étant donné un triangle ABC non équilatéral d'orthocentre H, notons O le centre de son cercle circonscrit et G son centre de gravité. Dans ces conditions, la droite (OH) contient G et on a :

OH = 3OG, ce qui peut s'écrire OH = OA + OB + OC

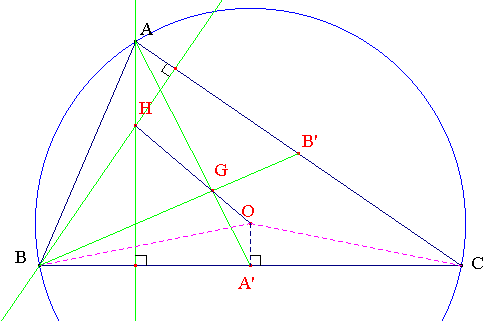
2/  Droite d'Euler :   

Le centre de gravité G d'un triangle, son cercle circonscrit O et son orthocentre H sont donc alignés et il semble que Euler soit le premier à l'avoir remarqué : la droite (OH) contenant G est droite d'Euler.

3/  Cercle d'Euler :  

La droite d'Euler contient un autre point remarquable, à savoir le milieu de [OH], centre Ω d'un cercle passant par les pieds A', B', C' des médianes, les pieds A1, B1, C1 des hauteurs et les milieux K, L et M de [AH], [BH] et [CH] :

Ce cercle dit des neuf points, également nommé cercle médial fut improprement baptisé cercle d'Euler. Il devrait s'appeler cercle de Brianchon. On l'appelle également cercle de Feuerbach car ce dernier lui découvrit d'autres propriétés. Ces résultats semblent avoir été énoncés pour la première fois dans sa mécanique des solides Theoria motus corporum solidorum (1765) mais selon Coxeter & Greitzer, Euler ne s'intéressa en fait qu'à la propriété de cocyclicité du cercle orthique (passant par le pieds des hauteurs) et du cercle complémentaire (passant par les pieds des médianes). Brianchon, en 1820, et Poncelet, l'année suivante, apportèrent chacun une preuve de l'existence du cercle des neuf points. Feuerbach compléta ces résultats par son théorème relatif aux cercles exinscrits. Terquem se pencha également sur le sujet par des calculs analytiques.

En savoir plus sur ces relations et le cercle des neuf points (exercice corrigé) : »
 

Théorème de Euler-Descartes pour les polyèdres convexes :

Selon Hilbert, cette belle formule, dite souvent de Euler (1752) serait due en fait à Descartes :

où S, F et A désignent respectivement le nombre de Sommets, de Faces et d'Arêtes d'un polyèdre convexe. De cette formule, on déduit facilement le résultat selon lequel :

Il n'existe que cinq polyèdres réguliers convexes : le tétraèdre (4 faces), le cube (6 faces), l'octaèdre (8 faces),
le dodécaèdre (12 faces) et l'icosaèdre (20 faces).

Preuve de ce résultat : »

Et cette belle formule s'applique au graphes planaires :

La théorie des graphes : » 

Précurseur avec Leibniz de la théorie des graphes et de la topologie, Euler résolut (1735) le problème des sept ponts de Königsberg (aujourd'hui Kaliningrad, Fédération de Russie) :

Partant d'un point de la ville, peut-on se promener en revenant à son point de départ, en passant une seule fois par tous les ponts ?

La réponse est non... graphe eulérien, théorie des graphes  : »            »  Berge , Cayley

 ∗∗∗ 
Quelques exercices sur les graphes, niveau Ter ES et SUP

• Euler intervint également en analyse statistique (problèmes d'ajustement) dans son traité des Inégalités du mouvement de Saturne et Jupiter :  » Mayer.

• Diagrammes d'Euler-Venn :  » Venn.

• Formule du binôme généralisée, parfois attribuée à Euler.

☼ Réponse exo : on peut écrire 8 = 2³ et 9 = 3²; donc : 2^x-1 = (2³)^y = 2^3y et 3^x-10 = (3²)^y-1 = 3^2y-2 et on a tout simplement : x - 1 = 3y et x - 10 = 2y - 2, d'où x = 22 et y = 7.

 ➔   Pour en savoir plus :

1. a) Œuvres complètes en français de Leonhardt Euler, publication de l'Ecole Militaire de Belgique (1839) sur Google Livres. Le volume 1, précédé de deux éloges (biographies) du célèbre mathématicien par Condorcet et Nicolas Fuss (1755-1826), mathématicien suisse :
   https://books.google.fr/books?id=aMkEAAAAYAAJ
   b) Introduction à l'analyse infinitésimale vol.1 (en français) : https://books.google.fr/books?id=288ndLD-p74C
   c) Introduction à l'analyse infinitésimale vol.2 (en français) : https://books.google.fr/books?id=Cxjkwu1G1T8C
   d) Les présupposés d'Euler dans l'emploi de la méthode fonctionnelle par Jean Dhombres sur le site Persée :
   https://www.persee.fr/doc/rhs_0151-4105_1987_num_40_2_4046
2. La fonction ζ de Riemann, par Javier Fresàn (un exposé remarquablement document) :
   http://jfresan.files.wordpress.com/2011/04/lecture-de-riemann.pdf
3. Théorème de Euler-Descartes : preuve de Lucas et autres développements dans la revue Quadrature n°4, juin 1990.
4. Une démonstration élégante de la formule d'Euler fut donnée par André Delachet dans La géométrie
   contemporaine, Collection Que Sais-je, n°401, P.U.F., 1950.
5. Courbure et caractéristique d'Euler-Poincaré d'une surface triangulée :
   http://www.math.ens.fr/culturemath/maths/pdf/geometrie/triang.pdf
6. a) Traité des intégrales eulériennes, Tome 2, Adrien Legendre sur Google Livres :
   https://books.google.fr/books?id=wy7vAAAAMAAJ&printsec=frontcover&hl=fr&source=gbs_ge_summary...
   b) Cours de mathématiques, tome II, par Jean Bass, Éd. Masson et Cie - Paris, 1964.
   c) Formule des compléments sur agreg-maths :
   https://agreg-maths.fr/uploads/versions/44/formule_complement_scourte.pdf
   c) Intégrales eulériennes : Cours d'analyse, Ch. V, par Jacques Harthong, ENS de Physique de Strasbourg :
   https://cel.archives-ouvertes.fr/cel-00519301v1/document
7. Les nombres premiers, Que sais-je n°571 (nouvelle édition 1997), par G. Tenenbaum & M. Mendès France
8. Répartition des nombres premiers par J.-L. Nicolas, Séminaire Delange-Pisot-Poitou :
   http://archive.numdam.org/article/SDPP_1967-1968__9_2_A12_0.pdf
9. Distribution des nombres premiers et fonctions zêta(s) par Hubert Delange (séminaire Delange-Pisot) :
   http://archive.numdam.org/article/SDPP_1959-1960__1__A1_0.pdf
10. a) Divergence  Σ1/p (p premier) des inverses des nombres premiers, somme équivalente à ln(ln(p)) sur The Euler Archive :
    https://scholarlycommons.pacific.edu/euler-works/72/
    b) ABRÉGÉ D'HISTOIRE DES MATHÉMATIQUES (1700-1900), Nombres premiers, ch. VI, par W. J. & F. Ellison
    Ouvrage collectif sous la direction de Jean Dieudonné, Éd. Hermann-1992
    c) La fonction zêta de Riemann, par Arnaud Dhallewyn (univ. Lille, 2013) : https://vixra.org/pdf/1406.0088v1.pdf  
11. Basel problem (la première résolution d'Euler en 1735), par Lucas Zanella : http://lucaszanella.com/en/articles/math/basel
    Voir aussi le diaporama de Weng Kin Ho, univ. NTU (Singapour) : http://math.nie.edu.sg/wkho/Talks_files/basel.pdf
12. a) Résolution du problème de Bâle proposé par Euler en 1743 (voir pages 10 et suivantes de la pagination pdf) :
    http://eulerarchive.maa.org/docs/originals/E063.pdf
    b) On the sums of series of reciprocals (1735) sur arxiv.org, calcul de ζ(2n) traduit du latin :
    https://arxiv.org/pdf/math/0506415.pdf
13. Liste des π(n) , 1 ≤ n ≤ 100 000 : https://oeis.org/A000720/b000720.txt
14. Développement asymptotique de la série harmonique (prépa. agrég. externe, X-ENS) :
    http://perso.eleves.ens-rennes.fr/~flemonni/agregation/developpements/Developpement.pdf
15. Biographie de Pietro Mengoli sur Treccani.it : http://www.treccani.it/enciclopedia/pietro-mengoli_(Dizionario-Biografico)

---

Buffon  Riccati Vincenzo

---

© Serge Mehl - www.chronomath.com