
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 ! On ne le confondra pas avec le mathématicien suédois
Harald Cramér
! On ne le confondra pas avec le mathématicien suédois
Harald Cramér
A la suite de brillantes études en mathématiques, physique et philosophie à l'Académie Calvin de Genève, sa ville natale, Cramer y enseignera la philosophie et les mathématiques dès l'âge de vingt (1724). Admirateur et ami de son compatriote Jean Bernoulli, passionné sur de nombreux sujets tant mathématiques que philosophiques, il voyagea à travers l'Europe à la rencontre des mathématiciens de sa génération déjà renommés comme Euler et Daniel Bernoulli installés à Saint-Pétersbourg à l'invitation de Pierre le Grand, Maupertuis, Buffon, philosophes et mathématiciens, Clairaut (qui se distingua dès 1726, âgé de 13 ans, dans l'étude des courbes algébriques...) en France, de Moivre en Angleterre, connu pour ses travaux en calcul des probabilités.
» L'Académie Calvin de Genève fut créée en 1559 par le théologien réformateur Jean Calvin (1509-1564) qui s'installa à Genève en 1541. L'Académie devint université en 1873.
Élu à l'Académie des sciences de Berlin (1746), il fut également membre de la Royal Society de Londres (1749). Cramer édita (par les soins de son cousin éditeur à Genève) les œuvres complètes de Jean et Jakob Bernoulli Ses travaux portent principalement sur les courbes algébriques et leur classification, la résolution des systèmes linéaires et le calcul des probabilités. Son cours de logique, professé à l'Académie Calvin, contenant des développements probabilistes, fut remarqué par d'Alembert lequel en intégra des éléments dans son Encyclopédie (» ref.2). En hiver 1751, malade, physiquement très diminué, Cramer espère retrouver une meilleure santé en se rendant dans le sud de la France, mais il meurt pendant le voyage à Bagnols sur Cèze dans le Gard, le 4 janvier 1752, âgé de 48 ans.
| Le traité des lignes courbes algébriques, paradoxe de Cramer (1750) : |
Dans un important traité de plus de 650 pages, écrit en français, attestant plusieurs années de recherches, intitulé Introduction à l'analyse des lignes courbes algébriques (1750, » réf.1), Cramer étudie les courbes algébriques définies sous forme implicite, c'est à dire par une équation polynomiale en x et y du type f(x,y) = 0 en examinant leurs singularités (points multiples, rebroussement, points d'inflexion), leurs branches infinies, leurs asymptotes, leurs tangentes.
Concernant les points doubles, incluant les points de rebroussements, Cramer montre cet important résultat :
Une courbe algébrique de degré n possède au plus (n - 1)(n - 2)/2 points doubles ou de rebroussement.
Un très utile et pratique résultat de Cramer :
Lorsqu'une courbe algébrique contient l'origine O des coordonnées (l'équation ne contient pas de terme constant), alors la (ou les) tangente(s) en O sont déterminées en annulant la partie constituée des termes de plus bas degré de l'équation.
en bleu f(x,y) = x3y3 + 2x2 - y = 0 : tangente d'équation y = 0 en O (axe Ox);
en rouge f(x,y) = x4 + y4 + y2 - x2 = 0 (lemniscate) : deux tangentes y = ± x en O qui est un point double;
en vert f(x,y) = x4 + y4 + x2 - 3x = 0 : tangente d'équation x = 0 en O (axe Oy).
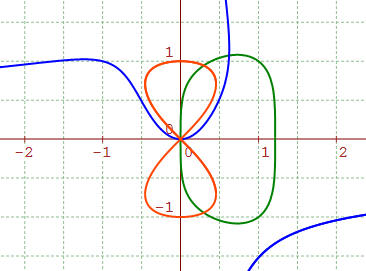
Points doubles, rebroussement, inflexion : » Tangentes à une courbe : »
| Paradoxe de Cramer : |
Deux courbes algébriques de degrés respectifs n et p se coupent en au plus np points
Ce résultat, énoncé auparavant par Maclaurin, fut prouvé par Bézout. Cramer le confirma tout en notant une anomalie du fait qu'une courbe algébrique de degré n est déterminée par au plus n(n + 3)/2 points, formule dite de Cramer mais avancée par Stirling dès 1717 :
Preuve de la formule : »
Mais cela est aberrant ! En effet, pour n = 3, par exemple, une courbe est déterminée par 9 points au plus et deux courbes du même degré se coupent en 9 points au plus (Maclaurin/Bézout). Ces 9 points, qui appartiennent aux deux courbes, ne peuvent caractériser l'une ou l'autre !
Bézout et Euler, sollicité par Cramer (» réf.4) expliqueront ce paradoxe en explicitant les règles de dépendance des points qui définissent les courbes algébriques et la solution complète sera donnée plus tard par Plücker dans sa théorie des courbes algébriques de 1839.
 Cas de l'ellipse :
»
ellipse
Cas de l'ellipse :
»
ellipse
On sait depuis la classe de 6ème (voire le CM2) que 3 points définissent un cercle unique. Mais :
Combien de points faut-il (en général) pour définir une et une seule ellipse ?
Les deux ellipses isométriques de la figure ci-dessus montrent que 4 points ne suffisent même pas : dans un repère orthonormé, les quatre points d'intersection appartiennent à chacune des ellipses considérées comme distinctes. La formule de Cramer permet d'affirmer que cinq points définissent une ellipse au plus. On peut vérifier ce résultat directement eu égard à l'équation générale des coniques (courbes algébriques de degré 2, englobant le cercle) :
Si a = 0, alors b est non nul et inversement. Dans ce cas, on peut diviser par b (ou bien par a); on est généralement en présence d'une parabole; il nous reste 4 paramètres et par suite 4 points seront nécessaires pour la déterminer sans ambiguïté
3 suffiront si le coefficient de xy est nul : axe parallèle à Ox ou Oy, cas auxquels on peut se ramener par changement de repère.
Si la courbe est un cercle de centre A(a,b), de rayon r, l'équation est (x - a)2 + (y - b)2 = r2, donc de la forme x2 + y2 + cx + dy + e = 0 : 3 coefficients, donc 3 points sont nécessaires et suffisants.
La formule de Maclaurin et la même figure montrent que deux ellipses se coupent en au plus quatre points. Le cas des cercles (n = p = 2) ne se coupant qu'en deux points au plus, montre également que les formules de Cramer et Maclaurin indiquent des bornes supérieures.
Courbe de Cramer, dite courbe du diable
:
»
| Système de Cramer (1748) : |
On appelle système de Cramer un système d'équations linéaires linéaire d'ordre n (n équations à n inconnues) ayant une unique solution (x1,x2,...,xn). Cramer donna une méthode de résolution équivalente à celle donnée par Cauchy dans les années 1810 au moyen de la théorie des déterminants. Avec cet usage, on peut définir un système de Cramer en tant que système d'équations linéaires n × n dont le déterminant est non nul. Cramer envisage les cas particuliers (indétermination, impossibilité) liés à des équations proportionnelles ou incompatibles (on trouvera le rappel de sa méthode en appendice I de son traité sur les courbes algébriques, »
réf.1b).Étant donné un tel système :
a1,1x1 + a1,2x2 + … + a1,nxn = b1
a2,1x1 + a2,2x2 + … + a2,nxn = b2
…
...
an,1x1 + an,2x2 + … + an,nxn = bn
on calcule son déterminant D; la solution est : (x1,x2,...,xn) = (D1/D , D2/D ,... , Dn/D) où Di est le déterminant obtenu en remplaçant la colonne de rang i par la colonne des constantes b1, b2, ..., bn. Le théorème de Rouché-Fontené traite le cas D = 0.
Un exemple d'ordre 3 :
Soit à résoudre le système :

1°) Vérifier par la règle de Sarrus que le
déterminant D du système est égal à -43. D est donc non nul : nous avons une
unique solution.
2°) Calculer Dx en remplaçant la "colonne des x" par la "colonne des
constantes". Vous devriez trouver 20 :
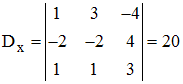
Calculer de même Dy et Dz. Finalement le système admet l'unique solution : x = -20/43, y = 57/43, z = 22/43.
➔ Matriciellement un système d'équations linéaires s'écrit AX = B. Si le déterminant de la matrice A, déterminant du système, est non nul, la solution est unique et s'exprime par X = A-1B. Si le déterminant de A est nul, A n'est plus inversible et le système peut ne pas avoir de solutions. Mais si B est nul, on a au moins la solution nulle; on parle de système homogène. Le déterminant d'un système homogène ayant une solution non triviale est nécessairement nul.
En pratique, la méthode de Cramer pour de "gros" systèmes n'est jamais utilisée (tout particulièrement en informatique) car coûteuse en temps de calcul (et généralement source d'erreurs). On lui préfère des méthodes d'approximations successives ou de triangulation de la matrice associée :
Méthode des pivots de Gauss : »
| Problème de Cramer-Castillon (ou problème de Pappus généralisé) : |
Il s'agissait d'un problème de construction géométrique :
Comment inscrire, dans un
cercle donné, un triangle dont les côtés (ou
leurs supports)
passent par trois points
donnés du plan ?

Le problème fut résolu par Castillon en 1776. On trouvera une solution de ce problème en référence 3 ci-dessous. La preuve de Castillon est présente en référence 4.
➔ Pour en savoir plus :