ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 CAYLEY Arthur,
anglais, 1821-1895 |
Arthur
Cayley naquit à Richmond lors d'un séjour de ses parents en Angleterre, car ces
derniers vivaient à Saint-Pétersbourg où le père travaillait pour une société
d'import-export. Après le retour de la famille (1829), Cayley étudiera au King's
College School de Londres où ses professeurs remarquent son aptitude aux
mathématiques. Mais la pression familiale le conduit à étudier le droit au Trinity College de Cambridge.
Devenu avocat, il exercera de 1849 à 1863 tout en se passionnant pour les langues (grec ancien, français, italien, russe, allemand) et les mathématiques : il publia dès l'âge de 20 ans des articles de mathématiques dans le Cambridge mathematical Journal.
Encouragé par son ami James Sylvester (avocat d'origine également), il étudie les mathématiques à Oxford (Angleterre) et Dublin (Irlande) et obtiendra une chaire de professeur de mathématiques à l'université de Cambridge (1867) qu'il conservera jusqu'à sa mort en 1895.
Membre de la Royal Society of London (l'Académie anglaise des Sciences) dès 1852, Cayley y publiera un grand nombre de ses travaux, notamment en géométrie projective où il s'intéresse à la définition d'une métrique projective (1859) et aux formes quadratiques qui généralisent la notion de distance dans les géométries non euclidiennes.
Ces recherches serviront à Klein pour définir les liens entre géométrie euclidienne, géométrie projective et géométries non euclidiennes (programme d'Erlangen, 1872). Durant les années 1860 et parallèlement à ceux de Clebsch en Allemagne, faisant suite à des travaux de Cramer et Plücker, on doit aussi à Cayley un important ouvrage sur une nouvelle classification des courbes algébriques planes faisant usage du concept de déficience, que Clebsch préféra appeler genre.
» Sextique de Cayley | Clebsch et le concept de genre d'une courbe ou d'une surface » Halphen
Mais l'œuvre maîtresse de Cayley sera le développement (dès 1838), avec Sylvester, d'une nouvelle branche des mathématiques : l'algèbre linéaire et ses transformations, nées de l'étude de la composition des transformations homographiques et des systèmes d'équations linéaires. L'ensemble, colossal, de ses travaux est réunie dans les Collected Mathematical Papers (13 volumes publiés entre 1889 et 1898). Tout comme Sylvester, outre la médaille De Morgan, il reçut la médaille Copley de la Royal society en 1882, une distinction en principe octroyé aux physiciens et biologistes.
| Calcul matriciel : |
Parallèlement aux travaux de Grassmann, Cayley dégage la notion d'espace vectoriel de dimension n, introduit, avec Sylvester, la notion de matrice (matrix, proposé par ce dernier en 1850) et en expose l'usage en faisant emploi des déterminants (dont l'initiateur fut Cauchy) dans une théorie plus large dite des invariants (1858) : on entend là des propriétés matricielles invariantes par transformation linéaire comme, par exemple, le déterminant, la trace (somme des éléments diagonaux).
Formes multilinéaires et déterminants : »
| Théorème de Cayley-Hamilton : |
Toute matrice carrée annule son polynôme caractéristique
C'est à Frobenius que l'on doit (1878) la démonstration rigoureuse de ce théorème.
Si M est une matrice carrée d'ordre n sur un corps K, le polynôme caractéristique P de M est le déterminant de la matrice λI - M, où I désigne la matrice unité :
Les valeurs propres de M sont les zéros de ce polynôme. En fait, la démonstration complète de ce théorème sera due ultérieurement à Frobenius.
Exemple :
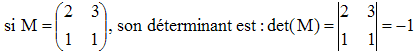
et son polynôme caractéristique :
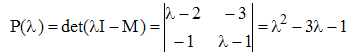
et on peut vérifier que si I désigne la matrice unité : M2 - 3M - I = 0.
Endomorphisme, polynôme caractéristique et polynôme minimal :
➔ Si M est la matrice d'un endomorphisme φ, on peut écrire φ2 - 3φ - id = 0 et on dira là encore que φ annule son polynôme caractéristique. On peut écrire P(φ) = 0. Le polynôme Π de plus bas degré annulant φ est appelé polynôme minimal de φ.
Les notations de l'algèbre des matrices :
On doit à Cayley la notation entre deux barres (1841) pour signifier un déterminant. Comme toute notation nouvelle, elle mit du temps à s'universaliser. Cayley lui-même utilisa des accolades { } en 1845 dans un article du Journal de Liouville...
Concernant la notation matricielle, usant aujourd'hui majoritairement de parenthèses, Cayley proposa, à la même époque (1843-45), les doubles barres || ||. Par exemple :
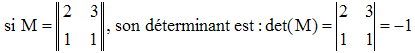
Au début du 20è siècle, Peano employa des crochets. Volterra écrivait par exemple, pour un système différentiel, cette notation condensée, très pratique : [dxi/dt] = [aik][xik] pour signifier :
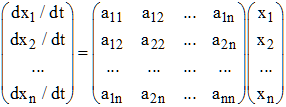
La notation entre [ ] et || || se retrouve encore de nos jours dans des publications russes ou anglo-américaines.
i En 1913, le mathématicien anglais Cuthbert Edmund Cullis (1875?-1955?), issu de l'université de Cambridge, enseigne à Calcutta. Son cours, Matrix and determinoids (1913) est un modèle de clarté et d'usage de notations adaptées au calcul matriciel : tableaux et écritures abrégées. On pourra consulter ce cours at this adress : http://www.archive.org/stream/matricesdetermin01cull#page/n15/mode/2up
| Nombres de Cayley, Algèbre des octonions : |
Deux années à peine après la "découverte" des quaternions d'Hamilton, l'anglais Cayley complète sa théorie algébrique des complexes avec l'introduction (1845) de "nombres" nouveaux. Il considère les couples de quaternions suivants :
e0 = (1,0), e1 = (i,0) , e2 = (j,0) , e3 = (k,0) , e4 = (0,1) , e5 = (0,i) , e6 = (0,j) , e7 = (0,k)
L'espace vectoriel réel de dimension 8 engendré par ces 8 couples est noté O; en le munissant du produit suivant :
O est une algèbre sur R, non commutative et non associative. Les éléments de O sont les octonions. On peut remarquer cependant que pour deux couples u et v d'octonions, on a :
(u × u) × v = u × (u × v) et u × (v × v) = (u × v) × v
On dit que l'algèbre O est alternative. C'est une propriété d'associativité affaiblie. Les 8 vecteurs de base de O sont parfois appelés nombres de Cayley.
On remarquera que pour tout i distinct de 0, on a ei2 = -1 et pour tout i et j non nuls : ei × ej = - ej × ei : on parle d'anticommutativité.
Hurwitz prouva (1898) que toute algèbre sur R, intègre, unitaire et normée est isomorphe à R, C, H ou O. Les octonions trouvent également leur usage en mécanique quantique (spin de l'électron).
| Le théorème des 4 couleurs, une application de la théorie des graphes : |
En 1872, Cayley présente la fameuse conjecture (1852) de l'écossais Francis Guthrie (1831-1899), un élève de de Morgan, concernant le coloriage des cartes géographiques de la Société Mathématique de Londres : il suffirait, au plus, de quatre couleurs pour que, quelle que soit la configuration géopolitique, deux pays ayant une frontière commune soient de couleurs différentes.
» clic on the map...
Une "preuve" donnée en 1879 par le mathématicien anglais Alfred Bray Kempe (1849-1922), ancien étudiant de Cayley au Trinity College, fut considérée comme juste jusqu'en 1890, année où l'un de ses compatriotes, Percy John Heawood (1861-1955), relève une erreur. Reprenant la démonstration de Kempe, Heawood montre alors que 5 couleurs suffisent dans tous les cas.
La preuve de la conjecture, pouvant se ramener à des courbes de Jordan s'intersectant sur une sphère (laquelle, privée d'un point, est homéomorphe au plan par projection stéréographique), relève de la topologie combinatoire et demande des connaissances approfondies en théorie des graphes. Elle conduit à des calculs combinatoires phénoménaux.
Un semblant de preuve put être menée à bien en 1976, après 4 années d'efforts, par les mathématiciens américains Kenneth Appel (1932-2013) et Wolfgang Haken (1928-2022, d'origine allemande) au moyen de l'ordinateur en ramenant le problème au coloriage d'un graphe planaire. Plus de 1200 heures de calcul et de nombreuses corrections et améliorations du programme de calcul. Cette "preuve" remet quelque peu en cause la notion même de démonstration mathématique : raisonnement par épuisement des cas, basé sur un programme informatique, laissé à un automate...
Même si la justesse du programme n'est pas remise en cause, les millions de calculs, voire des milliards, n'ont pas été vérifiés par un humain. Et si l'on recommence aujourd'hui ou demain pour vérifier, le doute sera récurrent... Certains mathématiciens, comme Coxeter n'admettent pas cette preuve informatique.
Paradoxalement, le nombre de couleurs, nombre chromatique, sur des surfaces plus subtiles que le plan, un tore par exemple, est plus facile à dénombrer : il fut prouvé qu'il est égal à 7.
|
Intégrale de Cayley : |
Il s'agit d'un exemple de calcul d'une intégrale double généralisée qui va s'avérer divergente. La fonction à intégrer ne gardant pas le même signe sur le domaine d'intégration, la méthode de calcul utilisée influe sur le résultat. Il s'agit donc d'être prudent lorsqu'on calcule un intégrale double généralisée sans avoir au préalable prouvé la convergence ! :
Soit à calculer :
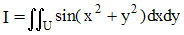
où U désigne le premier quadrant [0,+∞[ × [0,+∞[.
Si cette intégrale converge, on peut écrire :
»
Fubini
Mais x et y jouent des rôles identiques dans le calcul de I, donc :
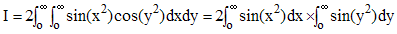
On reconnaît ici les intégrales de Fresnel, donc I semble être égale à π/4. Hélas, recalculons I en passant en coordonnées polaires (r,θ). Le produit dxdy devient égal à rdrdθ (» intégrale double) et U correspond à r variant de 0 à l'infini avec 0 ≤ θ ≤ π/2 :
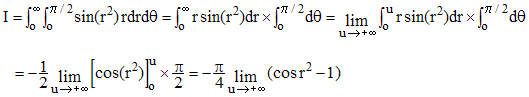
On constate donc la non convergence de notre intégrale car cos r2 oscille entre - 1 et 1. La valeur π/4 trouvée précédemment n'est donc que trompeuse !
| Cayley et la théorie des groupes : |
Cayley étudia les groupes abstraits finis dont il donne (1854) une définition axiomatique formelle qui sera complétée par lui-même (1878 et par les travaux de Frobenius, de Weber et Burnside. Jusqu'ici les groupes étaient observés sur des exemples, tout particulièrement depuis Galois avec les groupes de substitutions (permutations sur un ensemble fini) dont l'étude fut approfondie par Cauchy.
Ce sont donc des groupes finis. L'étude des groupes infinis apparaîtra avec Jordan puis Klein et Lie.
| Un important théorème de Cayley : |
Tout groupe fini d'ordre n est isomorphe à un sous-groupe du
groupe symétrique Sn
(lequel possède n! = 1 × 2
× ...
× n
éléments)
Notions sur les structures algébriques : » Métrique de Cayley : »
| Sextique de Cayley : |
Il s'agit d'une courbe algébrique de degré 6, podaire de la cardioïde par rapport à son point de rebroussement.
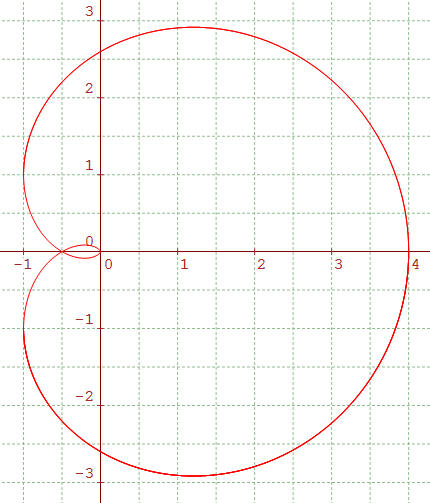
Étude de la courbe : »
➔ Pour en savoir plus :
Heine
