ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Formule de Wallis & calcul de π          » Version fonctionnelle récursive

On se propose de prouver ici la formule de Wallis, cas particulier de celle d'Euler :

et de la programmer sur tableur. Rappelons l'intégrale de Wallis :

      (w)

Etablissons tout d'abord une formule de récurrence entre I_n et I_n-2 :

• En classe de Terminale S, on calculera la fonction dérivée de x→sin^n-1x.cosx, ce qui fera apparaître sinⁿx et sin^n-2x...
• Au niveau Bac+1, au moyen d'une intégration par parties, utilisant sinⁿx = sin^n-1.sinx et en posant u =  sin^n-1 et v' = sinx, donc u' = (n - 1)sin^n-2x.cosx  et v = - cosx, on obtient :

Le terme tout intégré est manifestement nul. On remarque que cos²x = 1 - sin²x, ce qui conduit immédiatement à la formule :

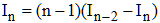
et donc, à la formule de récurrence :

En distinguant n pair ou impair et vu que I_o = π et I₁ = 2, on en déduit :

La suite (I_n) est clairement positive et décroissante car, pour cette dernière propriété :

Par suite :

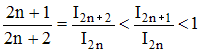
Ces résultats montrent que le rapport I_2n+1/ I_2n tend vers 1 par valeurs inférieures et donc que le produit infini :

tend vers par π/2 valeurs inférieures, soit :

avec e_n> 0 , tendant vers 0 lorsque n tend vers l'infini. La formule annoncée s'obtient alors par regroupement des termes.

• Colonne A : Le compteur n. Au départ n = 1, puis on incrémente de 1 et on recopie vers le bas autant que voulu.

• Colonne B : On calcule les numérateurs 4n² = (2n)².

• Colonne C : On calcule les dénominateurs 4n² - 1 et on recopie la formule vers le bas autant que précédemment.

• Colonne D : En D1, on écrit le premier terme du produit multiplié par 2 (sinon on obtiendrait une approximation de π/2). En D2, on écrit la formule itérative qui sera recopiée vers le bas : le produit de rang n (D2, D3, Dn...) est obtenu en multipliant le produit partiel de rang n - 1 précédent (D1) par 4n² et en le divisant par 4n² - 1.

Exemple d'exécution :

La convergence vers π est lente. Outre la lenteur de convergence, il se greffe des erreurs d'arrondi cumulatives générées par l'ordinateur. Si ε désigne la précision de la machine, on peut calculer que l'erreur à la n-ème itération est de l'ordre de 2nε, ce qui est fort inquiétant. L'algorithme n'est pas stable : l'erreur augmente avec n.

---

 ➔  Pour en savoir plus :

• Sur le site Maths-France.fr, on pourra consulter le sujet de CAPES 2009 consacré à l'intégrale de Wallis et à la formule de Stirling
  ainsi que le corrigé rédigé par Jean-Louis Rouget :
  - https://www.maths-france.fr/Capes/Capes_2009_M1_Enonce.pdf
  - https://www.maths-france.fr/Capes/Capes_2009_M1_Corrige.pdf
  Voir aussi : https://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/Integration/IntegralesDeWallis.pdf