
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
1. La première approche de la fonction exponentielle utilise la fonction logarithmique introduite ici par intégration de la fonction hyperbolique x→1/x. Cette approche était proposée aux élèves de Terminale jusqu'au début des années 1990. Elle permet d'obtenir les principales propriétés de la fonction x → ex.
2. La seconde approche (niveau sup) est une construction en tant que fonction dérivable égale à sa propre dérivée et utilise la formule de Taylor-Maclaurin. Elle permet de définir le logarithme népérien d'un nombre strictement positif en tant qu'unique solution de l'équation ex = m ⇔def x = ln(m).
3. Une
troisième approche en tant
qu'homomorphisme dérivable de (R,+) dans (R,×)
en recherchant les fonctions dérivables f vérifiant f(x + y) = f(x) × f(y)
avec la condition
f![]() '(0) = f(0).
Cette approche, relativement simple, conduisant immédiatement à
f
'(0) = f(0).
Cette approche, relativement simple, conduisant immédiatement à
f![]() ' = f,
apporte la solution à la question :
' = f,
apporte la solution à la question :
Existe-t-il une fonction dérivable d'une variable réelle qui, tout comme les fonctions puissances entières n → an, transforme une somme en produit : l'image d'une somme est le produit des images ?
La condition f
'(0) = f(0) fournit l'unique solution f(x) = ex. On pourrait, plus généralement, construire de façon analogue la fonction exponentielle de base a : x → ax (a > 0, a ≠ 1). Mais ces fonctions sont plus simplement définies à partir de ex au moyen ax = exlna.
ex et les fonctions exponentielles de base a : »
4. Suite géométrique et fonction exponentielle : supposons enfin qu'un phénomène A étudié numériquement soit à variation continue : A est mesuré en fonction d'un paramètre numérique x quelconque pouvant être un temps, une distance, une température, etc. Lorsque l'accroissement prévisionnel de A entre deux mesures proches m(x) et m(x + h) s'avère être proportionnel à sa mesure actuelle m(x), on constate que les variations de A sont régies par une fonction exponentielle du type x→ m(x) = k.eax. Suivez ce lien :
Suite géométrique et fonction exponentielle : »
♦ #1. La fonction exponentielle en tant que fonction réciproque du logarithme népérien :
On suppose ici connu la fonction logarithme népérien x → ln x, ainsi que ses propriétés, obtenue par intégration de la fonction hyperbolique t → 1/t :
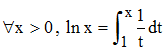

Continue, strictement croissante sur R+* = ]0,+∞[, cette fonction logarithme établit une bijection de R+* sur R tout entier. Elle admet donc une fonction réciproque continue, strictement positive et strictement croissante sur R, que nous notons exp(x), exp pour exponentielle, comme le fit Leibniz en 1695, appellation qui prendra son sens ci-après.
Premières propriétés et nombre e :
∀ x ∈ R : exp(x) > 0;
∀ x > 0 : exp(ln x) = x;
∀ x ∈ R : ln(exp(x)) = x.

La fonction ln est dérivable sur R+*, de dérivée x → 1/x distincte de 0 en tout point. Eu égard à la formule de dérivation des fonctions composées, la fonction exponentielle est dérivable sur R, de dérivée x → exp'(x) vérifiant exp'(x) × 1/exp(x) = 1, donc exp'(x) = exp(x).
La fonction exponentielle est égale à sa fonction dérivée
exp(0) = 1
 en remarquant que cette limite est exp'(0).
en remarquant que cette limite est exp'(0).
On note e (e pour exponentielle...)
l'unique réel strictement positif tel que ln e = 1. On a donc exp(1) = e. Cette
existence et son unicité sont
justifiées par les considérations précédentes sur la fonction logarithme.
L'étude de la courbe
x
→ ln x
indique 2 < e <3.
Propriétés algébriques :
exp(a + b) = exp(a) × exp(b) preuve en comparant les logarithmes népériens de chaque membre;
exp(a - b) = exp(a)/exp(b) preuve en comparant les logarithmes népériens de chaque membre;
exp(-x) = 1/exp(x) en remarquant par exemple que - x = 0 - x;
exp(n) = en pour tout entier n en procédant par récurrence.
exp(nx) = (ex)n pour tout entier n en procédant par récurrence.
exp(1/n) = e1/n pour tout entier n non nul en remarquant que e = exp(1) = exp(n × 1/n).
exp(a/b) = [exp(1/b)]a = [e1/b]a = ea/b pour tout a de Z et tout b a de N*.
Donc, selon cette dernière propriété :
Pour tout rationnel q = a/b, exp(q) = eq = ea/b
Soit maintenant un nombre réel x quelconque. Il est, par construction, la limite d'une suite qn de rationnels et, par continuité de la fonction exponentielle :

C'est donc e exposant
x, d'où son nom de fonction exponentielle
On donne ainsi, de façon naturelle, un sens à une puissance quelconque du nombre réel transcendant e, lequel vaut approximativement 2,7182818.
Autres fonctions exponentielles : » Calculs du nombre e dans ChronoMath : »
♦ #2. La fonction exponentielle en tant que fonction dérivable coïncidant avec sa dérivée
Notons f une fonction dérivable sur R
et coïncidant avec sa dérivée : f =
f![]() ' et vérifiant
f(0) = 1. Cette
fonction est alors indéfiniment dérivable. Dans tout voisinage V de zéro, une
telle fonction admet un développement en
série de Maclaurin convergeant vers f(x), x
∈V. En effet, le cas
général, à l'ordre n, s'écrit :
' et vérifiant
f(0) = 1. Cette
fonction est alors indéfiniment dérivable. Dans tout voisinage V de zéro, une
telle fonction admet un développement en
série de Maclaurin convergeant vers f(x), x
∈V. En effet, le cas
général, à l'ordre n, s'écrit :
![]()
soit ici :
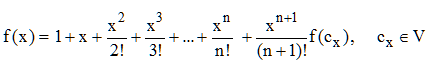
et la série converge pour tout x car le reste Rn(x) = f(cx) × xn+1/(n + 1)! tend vers 0, factorielle n l'emportant, pour n infini, sur toute puissance de x (» croissances comparées log, expo, xn, n!).
On voit ainsi que f existe et est unique. La fonction f est appelée fonction exponentielle et notée exp. On appelle e le nombre exp(1), c'est à dire :
e = 1 + 1/1! + 1/2! + 1/3! + ... + 1/n! + ...
On voit ainsi que e est de l'ordre de 2,7.
Calculs approchés de e : »
Propriété fondamentale :
Considérons la fonction φ définie pour tout réel x par φ(x) = exp(a + b - x) × exp(x), a et b désignant des réels quelconques. La fonction φ est dérivable et la règle de dérivation des fonctions composées permet d'écrire φ'(x) = - exp(a + b - x) × exp(x) + exp(a + b - x) × exp(x) = 0. Donc φ est constante sur R. On a φ(b) = exp(a) × exp(b), φ(0) = exp(a + b) × exp(0) = exp(a + b) et φ étant constante, on conclut :
∀ (a,b)∈R2, exp(a + b) = exp(a) × exp(b)
Cette propriété fondamentale permet de retrouver les résultats énoncés dans la première approche et de pouvoir écrire finalement :
exp(x) = ex = 1 + x/1! + x2/2! + x3/3! + x4/4! + ... + xn/n! + ... (1)
exp(-x) = e-x = 1/ex = 1 - x/1! + x2/2! - x3/3! + x4/4! + ... + (-1)nxn/n! + ... (2)
➔ On remarquera que l'on peut affirmer la (stricte) positivité de ex pour tout x de R. En effet, on peut écrire :
ex = ex/2 + x/2 = ex/2ex/2 = (ex/2)2
La fonction exponentielle selon Euler : »
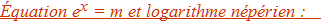
La fonction exponentielle est strictement positive et égale à sa dérivée. Elle est donc strictement croissante sur R. Sa limite en +∞ est clairement infinie selon (1). Sa limite en -∞ est donc 0 vu que e-x = 1/ex.

Dans ces conditions, l'équation ex = m, m > 0, admet une unique solution pour tout x réel. On note ln(m) cette solution, appelée logarithme népérien de m. On a donc l'équivalence :
ex = m, m > 0 ⇔ x = ln(m), m > 0 (3)
En particulier : e1 = e
⇔ 1 =
ln(e) et e0 = 1
⇔ 0 =
ln(1).
La relation fondamentale (3) ci-dessus permet d'écrire :
∀ x > 0, exp(ln(x)) = x ou encore avec la notation exponentielle : eln(x) = x
Le résultat 1, obtenu ici, relatif aux bijections réciproques permet d'affirmer que ln = (exp)-1. On a donc :
∀ x ∈ R+*, exp(ln(x)) = x et ∀ x ∈ R, ln(exp(x)) = x
En notation exponentielle : eln(x) = x et ln(ex) = x.
➔ Conformément à la pratique courante lorsqu'il n'y a pas de confusion possible, ln(x) s'écrit ln x. L'écriture ln x2 signifie ln(x2) et non pas (ln x)2. bien évidemment le logarithme de x + 1 doit s'écrire ln(x + 1).
On voit donc que cette méthode permet une définition du logarithme népérien comme alternative à sa définition par intégration de la fonction h(x) = 1/x. La propriété fondamentale ln(ab) = ln a + ln b et ses conséquences peuvent être obtenues par une petite astuce (même lien) ou à partir de l'exponentielle car exp(ln(ab)) = ab et exp(ln a + ln b) = exp(ln a) × exp(ln b) = ab, et l'exponentielle étant bijective, des images égales ont des antécédents égaux, d'où la formule annoncée
La fonction logarithme népérien : »
♦ #3. La fonction exponentielle en tant qu'homomorphisme de (R,+) sur (R,x)
On recherche une fonction f non nulle, dérivable sur R telle que :
i/ On a f(0) = f(0)2. Donc f(0) = 0 ou f(0) = 1. Si f(0) = 0, alors f(x + 0) = f(x) × f(0) = 0 pour tout x, donc f est nulle. En conséquence f(0) = 1.
ii/ Pour tout y fixé, dérivons par rapport x dans 1 : on a
f![]() '(x + y) =
f
'(x + y) =
f![]() '(x) × f(y).
Si x = 0, on obtient
f
'(x) × f(y).
Si x = 0, on obtient
f![]() '(y) =
f
'(y) =
f![]() '(0) × f(y)
pour tout y. La relation 2 permet d'écrire
f
'(0) × f(y)
pour tout y. La relation 2 permet d'écrire
f![]() '(y) = f(y) pour
tout y. Donc, si f existe, alors
f
'(y) = f(y) pour
tout y. Donc, si f existe, alors
f![]() ' = f.
' = f.
iii/ Quel que soit x, f(x - x) = f(0) = 1 = f(x) × f(-x).
Donc f(-x) = 1/f(x).
4i/ Quels que soient x et y, f(x - y) = f(x) × f(-y).
Donc f(x - y) = f(x)/f(y).
5i/ Posons f(1) = e. Quel que soit n de N, f(n) = f(1)n
= en (procéder
par récurrence)
6i/ f(nx) = [f(x)]n
pour tout entier n en procédant par
récurrence.
7i/ Quel que soit n de N, f(1/n) = e1/n
en remarquant que e = f(1) = exp(n × 1/n).
8i/ Pour tout a de Z et tout b a de N*,
f(a/b) = [f(1/b)]a =
[e1/b]a =
ea/b.
➔ à ce stade, on a retrouvé les propriétés découvertes par la première méthode. On est en droit de poser f(x) = ex pour tout x réel, avec e = f(1).
La relation f(x + y) = f(x) × f(y)
permet d'écrire que pour tout x, f(x) = f(x/2 + x/2) = [f(x/2)]2
> 0. f ne s'annule donc pas sur R. Vu que
f![]() ' = f, on déduit
que la fonction exponentielle est strictement croissante.
' = f, on déduit
que la fonction exponentielle est strictement croissante.
En conclusion :
Les trois approches étudiées conduisent (bien
heureusement) à une même fonction (exponentielle). Montrons l'unicité d'une
fonction f, dérivable telle que
f![]() ' = f et f(0) =
1.
' = f et f(0) =
1.
Si deux telles fonctions f et g existent, on a
en particulier g(x) > 0 pour tout x de R. Considérons la fonction f/g :
elle est dérivable et (f/g)'(x) = [f![]() '(x)g(x)
- f(x)g'(x)]/g(x)2 = 0 pour tout x. Donc f/g
est constante. Or f(0) = g(0) = 1, d'où f(x)/g(x) = 1 pour tout x : f = g.
'(x)g(x)
- f(x)g'(x)]/g(x)2 = 0 pour tout x. Donc f/g
est constante. Or f(0) = g(0) = 1, d'où f(x)/g(x) = 1 pour tout x : f = g.
Fonctions exponentielles de base a : » Suite géométrique et fonction exponentielle : »