Tangente & normale à une courbe

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Tangente & normale en un point d'une courbe
     » Cas polaire , cas paramétré x = f(t), y = g(t) , cas implicite f(x,y) = 0
             Point de rebroussement : cas y = f(x) , cas f(x,y) = 0 , cas paramétré x = f(t), y = g(t)
            Inflexion : cas y = f(x) , cas f(x,y) = 0 , cas paramétré x = f(t), y = g(t)

La seconde moitié du 17è siècle fut un période féconde pour le calcul différentiel et intégral que Newton et Leibniz érigeront en une des plus fécondes théories mathématiques établies jusque là. Wallis fut en Angleterre un des pionniers en la matière. En France, les premiers travaux sur les tangentes aux courbes peuvent être attribués à Pascal qui parlait de touchantes; on peut également citer, vers la fin du siècle, le marquis de l'Hospital.

L'exemple le plus élémentaire d'une tangente à une courbe sont les tangentes à un cercle : elles touchent le cercle sans le "couper". La normale en un point d'un cercle est la perpendiculaire à la tangente en ce point et passe par le centre du cercle.

∗∗∗ Tangente au cercle

Taux d'accroissement et dérivée d'une fonction y = f(x), tangente et normale en un point :

Au 18è siècle, d'Alembert ne se satisfait pas du concept d'infiniment petit de Newton et Leibniz, notion effectivement assez floue et pouvant entraîner de grosses erreurs dès lors qu'on estime pouvoir négliger des parties infinitésimales : infiniment petites.

Calcul différentiel selon l'Encyclopédie de Diderot et d'Alembert : »

On doit ainsi à d'Alembert la définition d'un nombre dérivé en tant que valeur limite, lorsque y est fonction f de x, d'un taux d'accroissement, sous la forme équivalant de nos jours à :

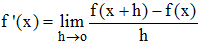
Toutefois, R n'est pas encore construit et il faudra attendre Weierstrass pour une définition rigoureuse du concept de limite.

! En posant h = Δx (accroissement de x) et Δy = f(x + h) - f(x), accroissement correspondant de f entre x et x + Δx, le nombre dérivé apparaît comme la limite de Δy/Δx lorsque Δx tend vers 0, ce qui conduit souvent à introduire "un peu rapidement" la différentielle par f'(x) = df/dx au prétexte qu'un Δx et un Δy "très petit" (infinitésimal) s'écrivent respectivement dx et dy. Ce n'est pas vraiment exact... :

Différentielle & application linéaire tangente : » Notion de limite selon d'Alembert : »

➔ On apprend au lycée que le taux d'accroissement, d'une fonction f sur un intervalle J = [a;b] de son ensemble de définition est l'accroissement de f sur cet intervalle ramené à une unité (taux) d'abscisse, soit :

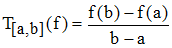
Ainsi, en notant (C) la courbe représentative de f, on reconnaît dans cette formule le coefficient directeur (la pente) d'une sécante (AB) à la courbe (C) : passant par les point A(a;f(a)) et B(b;f(b)).

Droites du plan, équations cartésienne et normale : »

Par suite, le nombre dérivé en x est la valeur limite, quand elle existe, lorsque h tend vers 0, des pentes des sécantes (s) coupant la courbe en deux points d'abscisses respectives x et x + h. La sécante (s) devient alors la tangente (T) en M(x,f(x)) :

Si f est dérivable en un point x, le nombre dérivé en x est le coefficient directeur de la tangente
en M(x, f(x)) à la courbe représentative de f

i C'est à Lagrange que l'on doit la notation f'(x) pour désigner cette limite, définissant ainsi la fonction dérivée et à Lhuillier l'abréviation lim allégeant la rédaction des calculs d'analyse.

➔ On appelle normale à une courbe en un point, la perpendiculaire à la tangente en ce point.

Calcul approché d'un nombre dérivé : » Fonction dérivée n-ème : »

Équation de la tangente et de la normale, cas explicite y = f(x) et implicite f(x,y) = 0

Cas d'une fonction explicite y = f(x) :

Lorsqu'une courbe (C) est définie par son équation cartésienne de la forme y = f(x), les considérations précédentes permettent d'affirmer que si f est dérivable en x_o, alors (C) admet une tangente au point M(x_o,y_o) qui a pour équation :

y - y_o = y'_o(x - x_o) ou bien : y = y'_o(x - x_o) + y_o avec y'_o = f '(xo)

Équation de la normale :

Si y'_o est nul, la tangente est parallèle à l'axe des abscisses (on parle souvent de tangente horizontale). Dans un repère orthonormé, la normale est alors parallèle à l'axe des ordonnées (normale verticale).
Si y'_o est non nul, la pente de la normale est alors -1/y'_o et son équation est y = - (x - x_o)/y'_o + y_o

D'une façon générale, dans un repère orthonormé, l'équation d'une droite (d) passant par M(x_o,y_o) peut être écrite sous la forme :

a(x - x_o) = b(y - y_o) , un vecteur directeur de (d) étant alors u(b;a).

v(-a;b) dirige alors la normale : en effet, le produit scalaire u.v est alors nul. Dans le cas présent nous avons u(1,y'_o) donc v(-y'_o,1) dirige la normale. En résumant :

Tangente en M_o : y'_o(x - x_o) = y - y_o , Normale en M_o : x - x_o = - y'_o(y - y_o)

Inflexion d'une courbe y = f(x) : »

Équation de la tangente dans le cas implicite f(x,y) = 0

Cas d'une fonction implicite f(x,y) = 0:

La différentielle de f est :

Mais f est nulle pour tout (x,y) de (C), donc df = 0. On applique le résultat ci-dessus y - y_o = y'_o × (x - x_o) où y'_o n'est autre que dy/dx. Par conséquent dy/dx = - ∂f/∂x ÷ ∂f/∂y. L'équation de la tangente est alors, les dérivées partielles étant calculées en (x_o,y_o) :

(x - x_o)∂f/∂x + (y - y_o)∂f/∂y = 0

Un vecteur directeur de la tangente (vecteur tangent) est u(- ∂f/∂y,∂f/∂x).

➔ Si la différentielle de f est nulle en M(x_o,y_o), ∂f/∂x = ∂f/∂y = 0, il s'agit d'un point stationnaire : point double ou multiple, rebroussement, inflexion. Le théorème suivant, dû à Cramer (1750) facilite souvent l'étude des tangentes en un tel point :

Si une courbe algébrique de degré n, définie par f(x,y) = 0, admet l'origine O des coordonnées comme point multiple non isolé, alors l'ensemble des tangentes en O est obtenu en annulant dans l'équation de la courbe l'ensemble des termes de plus bas degré (termes de degré au plus égal à n - 1).

Exemple : considérons la lemniscate de Bernoulli d'équation (x² + y²)² - 2a²(x² - y²) = 0 : on a ∂f/∂x= 4x(x² + y²) - 4a²x, ∂f/∂y = 4y(x² + y²) - 4a²y. Ces dérivées partielles sont nulles en (O(0,0). Les tangentes en O sont obtenues en annulant x² - y² : elles ont pour équation y = ± x.

Pour en savoir plus sur les points stationnaires des courbes algébriques dans le cas implicite voyez ces pages :

Points multiples d'une courbe f(x,y) = 0 : » Inflexion d'une courbe f(x,y) = 0 : »

Exemple d'étude de la tangente dans le cas implicite : soit la courbe d'équation f(x,y) = y + x³y³ - 2x² = 0 Calculer ∂f/∂x et ∂f/∂x. En déduire les équations des tangentes en x = 1 et x = - 1.On devra trouver y = x/3 + 2/3 et y = -x - 5/2. Ce que confirme le logiciel Graphmatica (remarquable et gratuit !) :

➔ Le cas explicite y = f(x) se ramène au cas implicite en posant y - f(x) = 0. Cette remarque peut s'avérer utile lorsque, connaissant un résultat applicable directement au cas implicite, on souhaite l'utiliser dans un contexte explicite.

Cas des coniques : » Théorème des fonctions implicites : »

Équation de la tangente et de la normale dans le cas paramétrique x = f(t) , y = g(t) :

Dans le cas d'une courbe paramétrée par x = f(t) et y = g(t), f et g étant supposées continument dérivables sur l'intervalle d'étude, sauf peut-être en des points isolés, la limite du taux d'accroissement Δy/Δx en un point M(x,y), correspondant à une valeur t_o du paramètre, peut s'écrire :

L'équation de la tangente est donc :

(x - x_o)g'(t_o) = (y - y_o)f'(t_o)

ou encore (forme ax + by = c) :

xg'(t_o) - yf'(t_o) = x_og'(t_o) - y_of'(t_o)

Un vecteur directeur de la tangente (vecteur tangent) est donc u(f'(t_o),g'(t_o)).

Cas singuliers :

si f '(t) est non nul, la pente de la tangente est m = g'(t)/f'(t), celle de la normale (n) sera -1/m si m est non nul, donc si g'(t) distinct de zéro. Sinon, la tangente est "horizontale" et la normale est "verticale".
si f '(t) = 0 et g'(t) ≠ 0 : il faut étudier de façon précise l'annulation de f ' au point t.
Si la limite de f' est nulle, il s'agira d'une tangente "verticale" et la normale sera "horizontale". Si une étude approfondie montre que les limites à droite et à gauche diffèrent, on parlera de demi-tangente verticale.
si f'(t) = 0 et g'(t) = 0 : le cas se complique :

Points stationnaires d'une courbe paramétrée : »

Équation de la normale :

Comme dit dans le cas cartésien, si l'équation de la tangente est a(x - x_o) = b(y - y_o) , un vecteur directeur est alors u(b;a) et v(-a;b) dirige la normale (en repère orthonormé). Dans le cas présent nous avons u(f'(t_o),g'(t_o)) donc v(-g'(t_o),f'(t_o)) dirige la normale. En résumant :

Tangente en M_o : g'(t_o)(x - x_o) = f'(t_o)(y - y_o) , Normale en M_o : f'(t_o)(x - x_o) = -g'(t_o)(y - y_o)

Équation de la tangente et de la normale dans le cas polaire r = f(θ) :

On peut se ramener au cas paramétrique en posant x = r.cosθ et y = r.sinθ. Dans les cas ordinaires, on vérifiera facilement, en procédant comme précédemment, que si r' désigne f '(θ), le coefficient directeur de la tangente est :

Mais cette formule est généralement peu pratique, mieux vaut calculer x'(θ) et y'(θ) :

le vecteur u(x'(θ_o),y'(θ_o)), vecteur tangent, dirige la tangente; son coefficient directeur est y'(θ_o)/x'(θ)
v(-y'(θ_o),x'(θ_o)) dirige la normale comme établi au cas précédent.

Exemple :

Quelle est l'équation de la tangente à la cardioïde d'équation r = -2 - 2cosθ au point θ = π/2 ? Passons en coordonnées paramétriques : x = (-2 - 2cosθ).cosθ , y = (-2 - 2cosθ).sinθ. D'où x' = 2sinθ + 2sin2θ , y' = -2cosθ - 2cos2θ. En θ = π/2, nous sommes en M(0;-2) et y'/x' = 1.
L'équation de la tangente est donc y = x - 2

Un résultat intéressant :

On sait que dans un repère orthonormé, le coefficient directeur m d'une droite est égal à la tangente de l'angle que fait cette droite avec l'axe (Ox) des abscisses. Soit Φ l'angle de la tangente au point M considéré avec le rayon vecteur OM d'axe polaire θ. On a :

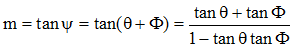
Dans la formule exprimant m ci-dessus, divisons les numérateur et dénominateur du second membre par r'.cosθ et identifions les deux formules exprimant m :

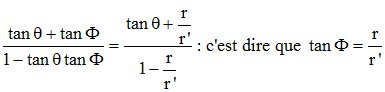
Point de rebroussement, tangente de rebroussement dans le cas cartésien y = f(x) :

On dit qu'une courbe plane admet un point de rebroussement lorsque la courbe présente une pointe et "rebrousse chemin" en présentant en ce point une même tangente qu'elle peut éventuellement traverser (1ère espèce et 2ème espèce) :

Cette notion est étudiée dans le cadre des courbes algébriques dans les cas implicite f(x,y) = 0 et paramétré x = f(t), y = g(t).

Dans le cas qui nous occupe, le rebroussement de 2ème espèce ne peut avoir lieu car tout élément x de l'ensemble de définition de f possède une image unique.

Dans le cas d'un rebroussement de 1ère espèce, la tangente au point de rebroussement est nécessairement verticale, sinon là encore un élément x aurait deux images.

En un tel point, la fonction n'est pas dérivable : le coefficient directeur de la tangente est infini.

Un exemple simple : la racine cubique de x²; c'est une fonctions paire. On peut écrire f(x) = (x²)^1/3 = x^2/3. On a donc :

» exposants fractionnaires

La racine cubique de x est du signe de x

Plus difficile : étude de la fonction irrationnelle :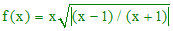

➔ Pages rattachées :

Différentielle et application linéaire tangente : »