
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


Vous trouverez ici les solutions d'une grande partie des exercices rencontrés dans l'ensemble des pages de ChronoMath repérés par le petit logo ∗∗∗ indiquant un exercice d'application d'un résultat ou d'une définition.
Des
exercices ou problèmes plus élaborés peuvent être consultés à partir de la page
d'accueil du site
rubrique EXOS CLG/LYC/SUP.

On calcule facilement A2 et A3 :

et on conjecture que An est de la forme :

Ce que l'on vérifie par récurrence en calculant An+1 = An × A en effectuant le produit :

On pose B = A - I où I désigne la matrice unité d'ordre 3. Calculer B2 et B3; en déduire An
On constate que tous les éléments de B2 sont nuls à l'exception du 1er élément de la colonne 3 et B3 = 0, matrice nulle. On a A = B + I et B commute avec I, matrice unité; par suite, on peut appliquer la formule du binôme au calcul de An = (B + I)n :
An = Bn + Cn1Bn-1 + Cn2Bn-2 + ... + Cnn-3B3 + Cnn-2B2 + Cnn-1B + I
Mais toutes les puissances de B sont nulles dès la troisième; il reste donc :
An = Cnn-2B2 + Cnn-1B + I = ½n(n - 1)B2 + nB + I

![]() f et g désignant deux endomorphismes, montrer que
toute valeur propre non nulle de f o g est aussi valeur propre de g o f.
f et g désignant deux endomorphismes, montrer que
toute valeur propre non nulle de f o g est aussi valeur propre de g o f.
Notons x un vecteur propre de f o
g associé à la valeur propre non nulle λ. On a (f
o
g)(x) = f(g(x) = λx.
D'où (g o
f)(g(x) = g(f(g(x)) = g(λx) = λg(x). Le vecteur g(x) est non nul
: sinon (f o g)(x) = λx = f(g(x)) =
f(0) = 0, ce qui impliquerait λ = 0 puisque x est on nul en tant que vecteur
propre de f o g. Par conséquent, λ
est valeur propre de g o f, de
vecteur propre associé g(x).
![]() Montrer que la fonction f(x) = (sin x)6 admet
x6 - x8 comme développement limité
d'ordre 8 au
voisinage de 0.
Montrer que la fonction f(x) = (sin x)6 admet
x6 - x8 comme développement limité
d'ordre 8 au
voisinage de 0.
On sait que, pour tout x, sin x =
x - x3/3! +x5/5! - x7/7! + ... On peut donc
écrire sin x = x - x3/6 + o(x3).
Ainsi (sin x)6
= (x - x3/6 + o(x3)]6. On applique la
formule du binôme au calcul de (x - x3/6)6
en tronquant le calcul à l'ordre 8.
➔ On a limité (!..) le développement limité de sin x à l'ordre 3 car, au-delà, les produits de la formule du binôme fourniront au moins du degré 10.
(x - x3/6)6 = x6 - C61x5x3/6 - C62x4(x3)2 + ... : le 3ème terme est (déjà) de degré 10. Par suite :
(x - x3/6)6 = x6 - C61x5x3/6
+ o(x8), soit : (sin x)6 = x6 - x8 + o(x8)
![]() Montrer que la fonction g(x) = ln(cos x) admet -x2/2 - x4/12
comme développement limité d'ordre 4 au voisinage de 0.
Montrer que la fonction g(x) = ln(cos x) admet -x2/2 - x4/12
comme développement limité d'ordre 4 au voisinage de 0.
On a :
g(0) = ln(cos 0) = ln(1) = 0
g'(x) = - tan x; g'(0) = 0
g"(x) = -1 - tan2x; g"(0) = - 1
g'''(x) = -2tan x - 2tan3x; g'''(0) = 0
g(4)(x) = -2 - 2tan2x - 6tan4x; g(4)(0) = -6
g(5)(x) = -16tan x(1 + tan2x) - 24tan3x(1 + tan2x); g(5)(0) = 0
g est infiniment dérivable en 0; les conditions d'application de la formule de Taylor sont vérifiées et on peut alors écrire :
ln(cos x) = -x2/2 - x4/12 + o(x4)
»
notation o(xn)
![]() Prouver par récurrence la formule : 13 +
23 + ... + n3 = (1 + 2 + ... +
n)2.
Prouver par récurrence la formule : 13 +
23 + ... + n3 = (1 + 2 + ... +
n)2.
On a :
n = 1 : 13 = 12
n = 2 : 13 + 23 = 1 + 8 = 9 = (1 + 2)2
n = 3 : 13 + 23 + 33 = 1 + 8 + 27 = 36 = (1 + 2 + 3)2
La formule semble bien fonctionner ! Procédons par récurrence en posant :
P(n) = « 13 + 23 + ... + n3 = (1 + 2 + ... + n)2 »
et tentons d'établir P(n + 1) : « 13 + 23 + ... + n3 + (n + 1)3 = [1 + 2 + ... + n + (n +1)]2 ».
On peut écrire :
13 + 23 + ... + n3 + (n + 1)3 = [13 + 23 + ... + n3] + (n + 1)3 = (1 + 2 + ... + n)2 + (n + 1)3
P(n + 1) sera établie si [1 + 2 + ... + n + (n +1)]2 - (1 + 2 + ... + n)2 = (n + 1)3. Le premier membre est une différence de carrés; or a2 - b2 = (a + b)(a - b). Par suite, sachant que 1 + 2 + ... + n = n(n + 1)/2 , notre différence est égale à :
[2(1 + 2 + ... + n) + (n + 1)](n + 1) = [n(n + 1) + (n + 1)](n + 1) = (n + 1)3
P(n + 1) est donc établie et la formule étant vérifiée pour n =
1, elle l'est donc pour tout n.
Le carré magique étant normal, tous les nombres de 1 à n2 apparaissent exactement une fois; il y a n x n = n2 cases; la somme des nombres utilisés est donc celle des n2 premiers entiers naturels, soit :
1 + 2 + ... + n2 = n2(n2 + 1)/2 » Nicomaque
Chaque ligne (ou colonne doit avoir la même somme, constante du carré, cette dernière est donc n(n2 + 1)/2. Par exemple, le carré magique normal (il est même diabolique...) d'ordre 4 ci-dessous a pour constante 4 x (16 + 1)/2 = 34 :

![]() Le nombre de candidats à un concours de la fonction
publique a évolué de la façon suivante :
Le nombre de candidats à un concours de la fonction
publique a évolué de la façon suivante :
|
Année |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
|
Nombre de candidats |
1170 |
1139 |
1023 |
980 |
942 |
847 |
716 |
a) Représenter le nuage de
points M(xi,yi)
où xi est le rang de l'année (xo = 0 pour 1997)
et yi
le nombre de candidats correspondant.
b) Ajuster linéairement le nuage par la méthode de Mayer
c) Quel est le nombre prévisible de candidats pour l'année 2004 ? Remarque ?
On peut mettre le tableau
statistique sous la forme :
| Année | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| Rang de l'année xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Nombre de candidats yi | 1170 | 1139 | 1023 | 980 | 942 | 847 | 716 |
a) et b) On regroupe les points en deux points moyens G1 et G2 : les 4 premiers en G1 (1,5 ; 1078) et les 3 derniers en G2 (5 ; 835). La droite de Mayer (G1G2) a alors pour équation y = -69,4x + 1182 (la valeur du coefficient directeur est une approximation à 0,1 près).

 c)
En admettant que l'ajustement par la droite de Mayer est acceptable, le nombre
prévisible de candidats pour l'année 2004 (rang 8) devrait être théoriquement
égal à y = -69,4 × 7 + 1182 = 696,2 :
c'est à dire de l'ordre de 700 candidats.
c)
En admettant que l'ajustement par la droite de Mayer est acceptable, le nombre
prévisible de candidats pour l'année 2004 (rang 8) devrait être théoriquement
égal à y = -69,4 × 7 + 1182 = 696,2 :
c'est à dire de l'ordre de 700 candidats.
Cependant, on constate que le dernier point (année 2003) est assez éloigné de la droite d'ajustement. Ce qui incite à penser que la linéarité décroissante des candidats s'est gravement accentuée en 2003 : c'est dire que l'ajustement n'est pas fiable (trop optimiste) et qu'une étude plus poussée devrait être entreprise.
Un ajustement polynomial par la méthode des moindres carrés : un ajustement du second degré fournit une prévision de seulement 630 candidats (y = -4,58x2 - 44,89x + 1168) . Le coefficient de corrélation linéaire reste cependant élevé : 0,984, ce qui n'est pas étonnant car seul le dernier point semble être l'intrus...
![]() Problème de
Syracuse : dans le cas impair, prouver que si l'on remplace :
tripler et ajouter 1 par simplement
ajouter 1, soit :
Problème de
Syracuse : dans le cas impair, prouver que si l'on remplace :
tripler et ajouter 1 par simplement
ajouter 1, soit :
if (n%2 == 0) {n = n/2} else {n = n + 1}
alors l'algorithme converge encore vers 1 en finissant également par 4 - 2 - 1.
Quel que soit le rang de
l'itération de l'algorithme, on est en présence d'un entier de la forme n = 2k
(cas pair) ou n = 2k - 1 (cas impair) avec k entier au moins égal à 1.
Si n = 2k, l'entier suivant est k = n/2 < n;
Si n = 2k - 1, l'entier suivant est 2k, donc le suivant est k =
(n + 1)/2 < n.
Ainsi, partant d'un entier n, on est assuré, en 1 ou 3
itérations, de poursuivre avec un entier p au plus égal à (n + 1)/2 < n.
Par suite au bout d'un nombre fini d'itérations, on atteint 1. En
effet, si la limite 1 n'est pas atteinte, alors elle vaut L > 1. L'entier L est
pair ou impair. Si L est pair, on peut le diviser par 2 : contradiction, la
limite n'est pas atteinte. Si L est impair, alors L + 1 est pair et (L + 1)/2 <
L puisque L > 1 : contradiction encore, la limite n'est pas atteinte.
Ainsi, 1 est bien atteint. Mais ce 1 ne peut provenir d'une forme
n + 1, donc il provient de n/2, donc de 2. Ce 2 ne peut pas non plus provenir
d'une forme n + 1 (il proviendrait alors de 1), donc il provient d'une forme
n/2, donc de 4 : la fin de l'algorithme est bien en
4 - 2 - 1.
➔
La
suite de ces entiers p est donc strictement décroissante et minorée par 1.
![]() On lance deux dés non truqués (faces numérotées de 1 à 6). Quelle est la probabilité p d'obtenir
un nombre (de 2 chiffres) qui ne soit pas divisible par 3 ?
On lance deux dés non truqués (faces numérotées de 1 à 6). Quelle est la probabilité p d'obtenir
un nombre (de 2 chiffres) qui ne soit pas divisible par 3 ?
Passons par l'événement contraire; le nombre obtenu est divisible par 3 si la somme de ses chiffres est multiple de 3 : donc 3, 6, 9 ou 12. Les couples "favorables" sont :
(1,2), (2,1), (1,5), (5,1), (2,4), (4,2), (3,3), (6,3), (3,6), (5,4), (4,5), (6,6)
La probabilité d'obtenir un nombre divisible par 3 est donc 12/36 = 1/3 et la probabilité cherchée est 1 - 1/3 = 2/3.
Passons par l'événement contraire : les élèves sont nés à des jours différents. On peut considérer la classe comme une liste classée arbitrairement :
Le nombre de cas possibles de la situation est 365 × 365 × 365 × ... × 365 = 36524 : chacun peut naître un jour quelconque de l'année.
Nombre de cas "favorables" : 365 jours s'offrent au 1er de la liste, 364 pour le second, ce qui fait donc déjà 365 × 364 cas. On poursuit jusqu'au 24è élève. Ce qui nous fera au total 365 × 364 × 363 × ... × 342 cas.
Vu l'équiprobabilité des éventualités, la probabilité de l'événement contraire est alors 365 × 364 × 363 × ... × 342 divisé par 36524. On peut calculer ce nombre avec une calculatrice ou un tableur, ce qui fournit sensiblement 0,46. On pourra aussi remarquer que 365 × 364 × 363 × ... × 342 s'interprète comme un arrangement de 365 objets pris 24 à 24 et utiliser le programme en ligne à la page Pascal fournissant A(365,24) = 1,443268... × 1061.
On a donc :
p = 1 - 365 × 364 × 363 × ... × 342 / 36524 ≅ 1 - 0,46 = 0,54
![]() Une une contient 12 boules dont 5 rouges, 3 noires, 2 vertes et 2 blanches.
Une une contient 12 boules dont 5 rouges, 3 noires, 2 vertes et 2 blanches.
a) On tire au hasard, successivement avec remise, 5 boules. Quelle est la probabilité d'obtenir 2 rouges, 2 noires et 1 verte ?
b) Retrouver cette probabilité en utilisant un raisonnement élémentaire du type
"cas favorables/cas possibles".
c)
Que devient la probabilité si le tirage est successif sans remise ?
d) Que devient la probabilité si le tirage des 5 boules est simultané ?
a) Si X désigne la variable aléatoire prenant comme valeur qualitative la couleur de la boule tirée, vu l'indépendance des tirages successifs et la pluralité des couleurs mises en jeu, on est en présence d'une loi multinomiale. Prob(R) = 5/12; Prob(N) = 3/12=1/4; Prob(V) = 2/12 = 1/6 = Prob(B). Notons E = Prob{on a obtenu 2R, 2N et 1V}. Selon la loi multinomiale :
Prob(E)
= Prob([R=2]∩[N=2]∩[V=1]∩[B=0])b) Vu qu'il y a remise de la boule tirée, à chaque tirage il y a 12 "cas possibles" compte non tenu de la couleur. L'épreuve admet donc 125 éventualités. Ce nombre s'interprète comme le nombre d'applications d'un ensemble C = {c1, ..., c5} de cardinal 5 (cinq cases) vers un ensemble U = {r1, r2, ..., r5, n1, n2, n3, v1, v2, b1, b2} de cardinal 12 (l'urne contenant les 12 boules).
Le nombre de "cas favorables" correspond aux permutations distinctes d'un quintuplet du type (R,R,N,V,N). Il y en a 5!/(2! × 2! × 1!) = 30. Chacun de ces quintuplets possède 52 × 32 × 2 = 450 façons de se réaliser. Le nombre de cas favorables est donc 30 × 450 = 13500. Et la probabilité de l'événement E est 13500/125 = 125/2304 @ 0,054.
c) Il n'y a pas remise de la boule tirée, les tirages successifs ne sont pas indépendants. On applique la règle des probabilités conditionnelles. Un arbre des éventualités fait comprendre que tous les quintuplets favorables, comme (R,R,N,V,N) ou (V,N,R,N,R), ont même probabilité de réalisation :
P(R) × PR1(R) × PR1R2(N) × PR1R2N3(V) × PR1R2N3V4(N) = 5/12 × 4/11 × 3/10 × 2/9 × 2/8 = 1/396
Il y a là encore 5!/(2!2) = 30 quintuplets de ce type. La probabilité de E est dans ce cas 30/396 = 5/66 @ 0,076.

Autre façon de raisonner :
En termes d'application de C vers U évoquée dans b), une épreuve s'apparente ici à une injection de C vers U car, par exemple r1 ne peut pas être tirée une seconde fois; il y en a A125 = 12 × 11 × 10 × 9 × 8 = 95040. Un cas favorable correspond à une injection comme (c1, ..., c5) → (r1, r2, n1, v1, n2). Un tel couple image répond à la question par tous les choix des rouges (C52), des noires (C32) et de la verte (C21) : 10 × 3 × 2 = 60 cas et par permutations de ses éléments : 5! = 120 cas. Soit au total 60 × 120 = 7200 cas favorables. Finalement, la probabilité de l'événement E est ici 7200/95040 @ 0,076.
d) En termes combinatoires, le nombre de cas possibles correspond au nombre de combinaisons de 5 objets parmi 12, soit (12 × 11 × 10 × 9 × 8)/120 = 792. Le nombre de cas favorables est le nombre de choix de 2 boules rouges parmi 5, 2 noires parmi 3 et 1 verte parmi 2, soit C52 × C32 × C21 = 10 × 3 × 2 = 60. La probabilité de E est dans ce cas 60/792 = 5/66 @ 0,076.
➔ La réponse est donc la même qu'en c). Normal, car choisir 5 boules simultanément revient à choisir une application de C vers U, c'est à dire 5 boules qui seront les 5 images en se restreignant aux injections (impossible de choisir 2 fois la même boule) et le dénombrement des cas favorables est le même que ci-dessus.
d divise n si n est un multiple de d. L'entier d étant premier, ces multiples sont d, 2d, 3d, ..., kd où k est le plus grand entier tel que kd ≤ ω! Mais d ≤ ω, donc d divise ω! finalement k = ω!/d et la probabilité cherchée est :
p = Card{d, 2d, 3d, ..., kd}/CardΩ = k/ω! = 1/d
La réponse n'est pas 1/2 comme on pourrait le penser un peu rapidement. La mise au monde des quatre enfants suit une loi binomiale de paramètre n = 4 et p = 1/2. En effet, pour ne pas tomber dans le piège sexiste, nous appellerons ici succès l'événement « naissance d'une fille » en s'intéressant à son nombre B d'occurrences.
Il s'agit alors d'une répétition de n = 4 épreuves indépendantes dont la probabilité de réalisation est p = 1/2. On sait que : Pr{B = k} = Cnk x pk x (1 - p)n - k. La probabilité cherchée est :
Pr{B = 2} : C42 ×
(1/2)2(1/2)2 = 6/16 = 3/8
On procède par récurrence et intégration par parties. Si n = 1 :

La convergence a lieu si et seulement si p > 0 : dans ce cas, dans le crochet, te-pt = t/ept tend vers 0. La dernière intégrale converge vers 1/p et finalement :
![]()
Pour n = 2, une double intégration par parties conduit (avec p > 0) à :
![]()
Pour n au moins égal à 1, Supposons vraie la formule :
![]()
On a :

C.Q.F.D.
Il s'agit de calculer l'intégrale de eate-pt (a et p réels ou complexes) sur [0,+∞[, c'est à dire celle de e(a - p)t, c'est à dire :
![]()
Si z est complexe et z = x + iy, ez = ex
x eiy. Le nombre eiy = cosy + i.siny
est borné : son module est 1.
Dans notre cas, si a - p est complexe, on voit que
l'intégrale sera convergente si et seulement si
Poser
![]() et
intégrer par parties :
et
intégrer par parties :
![]()
On a F(0) = 0 et, si p (resp. la partie réelle de p dans le cas complexe) est positif (resp. positive), alors le terme tout intégré est nul et LF(p) = Lf(p)/p. Le domaine de convergence est celui de Lf
.Poser u = at. On a :
![]()
D'où L(t
→
f(at)) = Lf(p/a)/a.
La convergence est assurée lorsque p/a est élément du
domaine de convergence de Lf.
![]() On note R1[x], l'ensemble
des polynômes unitaires (le coefficient du monôme de plus haute degré est 1)
d'une variable x à coefficients réels. Soit a et b deux polynômes de R1[x].
On dit que a divise b, s'il existe q dans
R1[x] tels que pour tout x, b(x) = a(x)q(x).
Montrer que l'on définit ainsi un ordre partiel dans R1[x].
On note R1[x], l'ensemble
des polynômes unitaires (le coefficient du monôme de plus haute degré est 1)
d'une variable x à coefficients réels. Soit a et b deux polynômes de R1[x].
On dit que a divise b, s'il existe q dans
R1[x] tels que pour tout x, b(x) = a(x)q(x).
Montrer que l'on définit ainsi un ordre partiel dans R1[x].
Réflexivité
:
∀a∈
R1[x], a non nul, a|a car
q(x) = 1
∀x est élément de
R1[x].
Antisymétrie :
si a|b et b|a, il existe q et q' dans
R1[x] tels que b = aq et a
= bq', par suite qq'(x) = 1
∀x
et, dans R1[x],
cette égalité implique d°qq' = d°q × d°q'
= 0 (polynôme constant), donc q et q' sont constants et étant unitaires, il
s'agit de q(x) = q'(x) = 1
∀x,
donc a = b.
Transitivité :
si a|b et b|c, il existe q et q' dans
R1[x] tels
que b = aq et c = bq', par suite c = aqq' avec qq'∈R1[x],
donc a|c.
![]() On note
Σ
k=1,n l'opérateur de sommation pour k variant de 1 à n. Prouver par
récurrence que pour n au moins égal à 2, on a :
On note
Σ
k=1,n l'opérateur de sommation pour k variant de 1 à n. Prouver par
récurrence que pour n au moins égal à 2, on a :
n! = 1 + Σ k=1,n-1 k × k! (pn)
La relation est vérifiée pour n = 2. Supposons la formule (pn) vraie pour un entier n au moins égal à 2.
(n + 1)! = (n + 1) × n! = n + nΣ k=1,n-1 k × k! + 1 + Σ k=1,n-1 k × k!
Or, par hypothèse de récurrence : n + nΣ k=1,n-1 k × k! = n + n(n! - 1) = n × n!
Par suite : (n + 1)! = 1 + n × n! + Σ k=1,n-1 k × k! = 1 + Σ k=1,n k × k!
CQFD.
![]() Trouver un système d'inéquations minimal (le
moins d'inéquations possibles) faisant usage de la valeur absolue et dont les
solutions sont les points intérieurs à l'octogone
ci-dessous
:
Trouver un système d'inéquations minimal (le
moins d'inéquations possibles) faisant usage de la valeur absolue et dont les
solutions sont les points intérieurs à l'octogone
ci-dessous
:

Ces 4 inéquations caractérisent l'octogone : | x | < 2 , | y | < 2 , | x
- y | < 3 , | x + y | < 3.
![]() Traduire en notations modernes cet extrait de l'Ars Magna
:
Traduire en notations modernes cet extrait de l'Ars Magna
:


Réponse : 32x2 + 16 + x4 = 48 et
1x4 + 32x2 + 256 = 48x + 240.
![]() Selon une légende, l'inventeur du jeu d'échecs aurait demandé comme récompense à
son souverain, enchanté par ce jeu, de lui offrir autant de grains de blé que
l'on compte sur un échiquier en en mettant 1 sur la première case, 2 sur la
seconde, 4 sur la troisième, et ainsi de suite en doublant. Tous les greniers du
royaume furent vidés sans pour autant satisfaire notre inventeur.
Combien de tonnes de blé seraient nécessaires en admettant un PMG (Poids de
Mille Grains) de 45 g ?
Selon une légende, l'inventeur du jeu d'échecs aurait demandé comme récompense à
son souverain, enchanté par ce jeu, de lui offrir autant de grains de blé que
l'on compte sur un échiquier en en mettant 1 sur la première case, 2 sur la
seconde, 4 sur la troisième, et ainsi de suite en doublant. Tous les greniers du
royaume furent vidés sans pour autant satisfaire notre inventeur.
Combien de tonnes de blé seraient nécessaires en admettant un PMG (Poids de
Mille Grains) de 45 g ?
Le nombre de grains est 1 + 2 + 4 + 8 + 16 + ... = 20 + 21 + 22 + 23 +24 + ... + 263 = 1 × (264 - 1)/(2 - 1) = 264 - 1. C'est un nombre énorme : 18 446 744 073 709 551 615. Nous l'arrondissons à 1,845 × 1019.
Cet arrondi se retrouverait en calculant
le logarithme décimal de 264, soit 19,26592 = 19 + 0,26592 et cette mantisse
correspond à 1,84467, d'où le résultat. Divisons par 1000 et multiplions par 45
(poids en grammes) et convertissons ensuite en millions de tonnes (1 Mt = 1012
grammes), soit 830 250 000 Mt. : c'est effarant, la production mondiale de blé
étant (seulement) de l'ordre de 600 Mt en 2004 !
A B A ⇒ B B ⇒ A A
⇔ B = (A ⇒ B
et B ⇒ A) V V V V V V F F V F F V V F F F F V V V![]() Quelle est la table de vérité de A
⇔ B ?
Quelle est la table de vérité de A
⇔ B ?
![]() Définir l'inclusion des ensembles au moyen de l'ensemble
vide et de la différence d'ensembles :
Définir l'inclusion des ensembles au moyen de l'ensemble
vide et de la différence d'ensembles :
A⊂B ⇔ A - B = Ø
![]() Montrer que si B = {b1, b2, ..., bn}
⊂ A, alors A -
B = ∩[A - {bk}], intersection des A - {bk},
k = 1, 2, ..., n .
Montrer que si B = {b1, b2, ..., bn}
⊂ A, alors A -
B = ∩[A - {bk}], intersection des A - {bk},
k = 1, 2, ..., n .
Vu que B est inclus dans A, pour tout k = 1, 2, ..., n, on a A -
{bk} =
![]() A{bk},
complémentaire de {bk} dans A.
A{bk},
complémentaire de {bk} dans A.
Selon les lois de Morgan, l'intersection des complémentaires des {bk}
dans A est le complémentaire de la réunion des {bk}
dans A, c'est à dire le complémentaire de B dans A, c'est à dire A - B.
![]() Montrer que (A |
A) | (A | A) et (A ↓ A)
↓ (A
↓ A) sont équivalentes à A.
Montrer que (A |
A) | (A | A) et (A ↓ A)
↓ (A
↓ A) sont équivalentes à A.
(A | A) | (A | A) s'écrit non[(A | A) et (A | A)], soit selon de Morgan : non(A | A) ou non(A | A), c'est à dire A ou A, soit A.
(A![]() A)
↓ (A
↓ A) s'écrit
non[(A
↓ A) ou
(A
↓ A)], soit
selon de Morgan : non(A
↓ A) et
non(A
↓ A), c'est à
dire A et A, soit A.
A)
↓ (A
↓ A) s'écrit
non[(A
↓ A) ou
(A
↓ A)], soit
selon de Morgan : non(A
↓ A) et
non(A
↓ A), c'est à
dire A et A, soit A.
Comment s'écrit A et B au moyen de NOR ↓ ?
A et B s'écrit (A | A) | (A | B) ou (A ↓ A) ↓ (B ↓ B), forme dite duale du ou.
A ⇒ B s'écrit A | (A | B). Et avec ↓ ?...
A ⇒ B peut s'écrire non[non(nonA ou B)], soit non(nonA ↓ B) qui s'écrit (nonA ↓ B) ↓ (nonA ↓ B). Mais nonA c'est A ↓ A. Donc A ⇒ B peut s'écrire :
[(A ↓ A) ↓ B)] ↓[(A ↓ A) ↓ B)]
si f est une fonction numérique croissante d'un intervalle [a,b] dans lui-même, alors il existe un réel c de [a,b] tel que f(c) = c.
Si f(a) = a, le résultat est démontré... Sinon, f étant croissante, on a f(a) > a. Notons E l'ensemble des x de [a,b] tels que f(x) > x. L'ensemble E est borné et non vide, il admet donc une borne supérieure m.
Montrons que f(m) = m. Si l'on suppose m < f(m), soit x réel, m < x < f(m). L'application f étant croissante, on a f(m) ≤ f(x) et par suite x < f(x). donc x est élément de E et m < x : incompatible avec m borne supérieure de E. Si l'on suppose maintenant m > f(m), soit x réel, f(m) < x < m. On applique f, ce qui conduit cette fois à f(x) < x. Par suite x n'est pas élément de E : il n'existe aucun élément de E entre f(m) et m. Or, pour tout x de E, on x ≤ m, donc x ≤ f(m) : m n'est pas le plus petit des majorants de E ! En conclusion m = f(m) : l'application f admet c = m comme point fixe.
![]() Quelle est la négation de :
∀ε > 0,
∃
p∈N,∀n∈N
, n > p ⇒
1/n < ε ?
Quelle est la négation de :
∀ε > 0,
∃
p∈N,∀n∈N
, n > p ⇒
1/n < ε ?
La négation de « ∀ε > 0, ∃ p∈N, ∀n∈N , n > p ⇒ 1/n < ε » est :
« ∃ ε > 0, ∀p∈N, ∃ n∈N , n > p, 1/n ≥ ε »
Cette négation est fausse : si on choisit p entier tel que 1/p <
ε, alors n > p
⇒ 1/n
< ε
car 1/n < 1/p (transitivité de la relation d'ordre).
![]() Afin de justifier les insuffisances de la logique
bivalente du tiers exclu, Brouwer donna plaisamment l'exemple du voyageur qui se
retrouve prisonnier chez des cannibales d'un un pays éloigné. Ses tortionnaires
lui proposent de réfléchir à son dernier vœu; cela devra être une phrase sensée
et vérifiable par le chef de la tribu : si c'est un mensonge, il sera bouilli,
si c'est une vérité, il sera rôti. Après réflexion, notre voyageur sauva sa peau
et le chef fut banni car il prit sa place... Pourquoi ?
Afin de justifier les insuffisances de la logique
bivalente du tiers exclu, Brouwer donna plaisamment l'exemple du voyageur qui se
retrouve prisonnier chez des cannibales d'un un pays éloigné. Ses tortionnaires
lui proposent de réfléchir à son dernier vœu; cela devra être une phrase sensée
et vérifiable par le chef de la tribu : si c'est un mensonge, il sera bouilli,
si c'est une vérité, il sera rôti. Après réflexion, notre voyageur sauva sa peau
et le chef fut banni car il prit sa place... Pourquoi ?
Le subtil voyageur a pu dire « je serai bouilli » ou « je ne serai pas rôti ». En effet, s'il dit par exemple « je serai bouilli », dans la logique du tiers exclu :
ou bien les cannibales le bouillent, auquel cas, il aurait dit une vérité et il aurait fallu le rôtir.
ou bien les cannibales le rôtissent, auquel cas, il aurait dit un mensonge et il aurait fallu le bouillir.
![]() Prouver que toute isométrie du plan admettant 2 points invariants (au moins) est
soit l'identité (id : M
→
M, ∀M), soit une symétrie axiale.
Prouver que toute isométrie du plan admettant 2 points invariants (au moins) est
soit l'identité (id : M
→
M, ∀M), soit une symétrie axiale.
Soit f l'isométrie en question, A et B deux points invariants par f, C un point
du plan non situé sur [AB]. f étant affine, remarquons déjà que (AB) est une
droite de points invariants. Si C est invariant, alors f laisse invariant un
repère du plan : f est donc l'identité (application identique id). Supposons
maintenant f(C) = D, D distinct de C. f étant une isométrie, on a AC = AD et BC
= BD. Par suite, (AB) est la médiatrice de [SD] : f est la symétrie d'axe (AB).
![]() Un bibliothécaire qui classait des annuaires s'aperçut que
certains se mentionnaient eux-mêmes et d'autres pas. Il se mit en tête de créer
deux nouveaux annuaires : Ann1
→ qui se
mentionnent eux-mêmes, Ann2
→ qui ne se
mentionnent pas eux-mêmes. En feuilletant Ann2, il se demanda où cet annuaire
devait se mentionner ?...
Un bibliothécaire qui classait des annuaires s'aperçut que
certains se mentionnaient eux-mêmes et d'autres pas. Il se mit en tête de créer
deux nouveaux annuaires : Ann1
→ qui se
mentionnent eux-mêmes, Ann2
→ qui ne se
mentionnent pas eux-mêmes. En feuilletant Ann2, il se demanda où cet annuaire
devait se mentionner ?...
Si Ann2 est mentionné dans Ann2 : Ann2 est alors un annuaire qui se mentionne lui-même dans la liste des annuaires qui ne se mentionnent pas : pas possible.
Si Ann2 est mentionné dans Ann1 : Ann2 est alors un annuaire qui se mentionne lui-même. C'est contradictoire quant à sa nature d'annuaire qui ne se mentionne pas : il devrait être dans Ann2...
![]() a) Vérifier que la transformée de Fourier de x
→ f(kx)
est w
→ 1/|
k | × F(w/k).
On distinguera k > 0 et k < 0.
a) Vérifier que la transformée de Fourier de x
→ f(kx)
est w
→ 1/|
k | × F(w/k).
On distinguera k > 0 et k < 0.
b) Calculer la transformée de Fourier de la fonction x
→ e-|x|.
c)
En
déduire celle de x
→ e-k|x|,
k > 0.
Vérifier par un calcul direct.
a) En négligeant ici le rapport 1/2p, la TF de
x
→ f(kx) est
l'intégrale sur R de f(kt)e-iwt.
On
pose alors u = kt.
Si k > 0, on obtient l'intégrale sur [-∞,+∞] de 1/k × f(u)e-iwu/k, soit 1/k × F(w/k).
Si k < 0, on obtient l'intégrale sur [+∞,-∞]
de 1/k × f(u)e-iwu/k,
soit l'intégrale sur [-∞,+∞]
de
-1/k × f(u)e-iwu/k
= 1/| k | × f(u)e-iwu/k.
D'où le résultat annoncé.
b) Le calcul est
très simple et conduit, en sommant les intégrales sur [-∞,o]
et [o,+∞],
à 2/(w2
+ 1), en négligeant là encore le 1/2p.
c) en négligeant toujours 1/2p,
un calcul direct conduit facilement à (k > 0) : 1/(k - iw)
+ 1/(k + iw) = 2k/(k2
+ w2)
= 1/k × F(w/k).
![]() Au lancer d'un dé (dont les faces
sont numérotées de 1 à 6), on mise 1 euro et il est associé :
Au lancer d'un dé (dont les faces
sont numérotées de 1 à 6), on mise 1 euro et il est associé :
un gain de 1€ si le 1 ou le 2 apparaît;
un gain de 5€ si le 6 apparaît;
un gain nul si le 5 sort;
une perte de 1€ pour les autres cas. La mise n'est pas récupérée. Quelle est l'espérance mathématique de gain ?
Aux gains bruts, on doit retirer 1 euro. On a alors en gains nets :
2 chances sur 6 de gagner 1 euro : gain = + 1 - 1 = 0, probabilité 1/3;
1 chance sur 6 de ne rien gagner : gain = 0 - 1 = - 1, probabilité 1/6;
2 chances sur 6 de perdre 1 euro : gain = -1 - 1 = - 2, probabilité 1/3;
1 chance sur 6 de gagner 6 euros : gain = + 5 - 1 = +4, probabilité = 1/6.
Noter l'aspect mathématique d'un gain : il peut être négatif et est alors synonyme de perte.
L'espérance de gain est :E = 0 × 1/3 - 1 × 1/6 - 2 × 1/3 + 4 × 1/6 = -1/6
L'espérance de gain est négative, de l'ordre de 17 centimes. Cela ne signifie que, en moyenne mathématique théorique, en jouant un grand nombre de fois, votre perte sera de l'ordre de 17 centimes. Mais on peut fort bien gagner plusieurs fois de suite et quitter la table...
![]() On suppose f positive et décroissante sur I = [a,+∞[
avec lim f = 0 pour x infini; g est une fonction intégrable et bornée sur
tout intervalle fini K de I et vérifiant |
On suppose f positive et décroissante sur I = [a,+∞[
avec lim f = 0 pour x infini; g est une fonction intégrable et bornée sur
tout intervalle fini K de I et vérifiant | g(x)|
≤ M, où
M désigne un
réel positif indépendant de K. Montrer que dans ces conditions l'intégrale
sur I du produit fg est convergente.
g(x)|
≤ M, où
M désigne un
réel positif indépendant de K. Montrer que dans ces conditions l'intégrale
sur I du produit fg est convergente.
Soit K = [x,x'] un intervalle fermé quelconque de J. Selon la seconde formule de la moyenne applicable ici au vu des hypothèses, il existe u entre x et x' tel que :

soit e > 0 arbitraire, si x est suffisamment grand, on aura f(x) < e/M et le membre de gauche peut être rendu inférieur à e : c'est la condition de Cauchy pour la convergence de l'intégrale généralisée étudiée.
![]() a/ L'équation ω = ydx + xdy - xydz est-elle exacte ?
a/ L'équation ω = ydx + xdy - xydz est-elle exacte ?
b/ Montrer que l'équation ydx + xdy - xydz = 0 est intégrable et
l'intégrer. Justifier l'existence d'un facteur intégrant et le calculer.
a/ On applique la
CNS pour que la forme proposée soit la différentielle totale d'une fonction
f(x,y,z).
On a ici P(x,y,z) = y, Q(x,y,z) = x et R(x,y,z) = -xy. ∂P/∂y = 1 =
∂Q/∂x, ∂Q/∂z = 0 ≠ ∂R/∂y = -x. ω n'est donc pas une forme différentielle exacte.
b/ On peut ici (forme homogène) considérer z comme fonction de x
et y en écrivant dz = dx/x + dy/y. On a ∂z/∂x = -P/R = 1/x et ∂z/∂y = -Q/R = 1/y. La première équation
fournit z = ln| x | + α(y) : la constante
d'intégration dépend de y.
D'où ∂z/∂y = 1/y = α'(y).
Par suite z = ln| x | + ln| y | + β(x).
En redifférenciant par rapport à x, il vient β(x)
= 0.
Finalement z = ln| xy | + C, C ∈ R.
En dimension 3, l'existence d'un facteur intégrant (x,y,z) → k(x,y,z) de ω est soumis à la condition :
Elle est clairement vérifiée : y(-x - 0) + x(0 + y) + xy(1 - 1) = 0. Dès lors k doit vérifier kP = ∂f/∂x, kQ = ∂f/∂y, kR = ∂f/∂z. Il apparait que k(x,y,z) = 1/xy et ω1 = kω = dx/x + dy/y - dz apparaît comme la différentielle totale de f(x,y,z) = z - ln| xy |.
![]() Résolution de l'équation différentielle d'Euler x2y"
+ xy' + y = 0, y(1) = 0, y'(1) = 1
» Voyez aussi
exercice 3
Résolution de l'équation différentielle d'Euler x2y"
+ xy' + y = 0, y(1) = 0, y'(1) = 1
» Voyez aussi
exercice 3
On pose t = ln![]() x.
Selon la théorie relative à la résolution de
l'équation d'Euler ax2y" + bxy' + cy = 0, on est ramené à
l'équation d'inconnue y, fonction de t : ay" + (b -
a)y' + cy = 0 avec x = et. En l'occurrence, a =
b = 1, c = 1. On résout donc y" + y = 0. L'équation caractéristique est r2
+ 1 = 0. Δ < 0 :
deux solutions complexes conjuguées r = u ± iv = ±
i (u = 0, v = 1). La solution générale est : y = xu[c1cos(v×ln
x.
Selon la théorie relative à la résolution de
l'équation d'Euler ax2y" + bxy' + cy = 0, on est ramené à
l'équation d'inconnue y, fonction de t : ay" + (b -
a)y' + cy = 0 avec x = et. En l'occurrence, a =
b = 1, c = 1. On résout donc y" + y = 0. L'équation caractéristique est r2
+ 1 = 0. Δ < 0 :
deux solutions complexes conjuguées r = u ± iv = ±
i (u = 0, v = 1). La solution générale est : y = xu[c1cos(v×ln![]() x) + c2sin(v×ln
x) + c2sin(v×ln![]() x)]
= c1cos(ln
x)]
= c1cos(ln![]() x) + c2sin(ln
x) + c2sin(ln![]() x).
Les conditions initiales conduisent à c1
= 0 et c2 = 1, d'où :
x).
Les conditions initiales conduisent à c1
= 0 et c2 = 1, d'où :
y = sin(ln(x) » Résolution approchée
![]() Concernant l'équation de Kepler : Vérifier que
tan j
= (1 - e2)½cos e/(cos e-
e)
Concernant l'équation de Kepler : Vérifier que
tan j
= (1 - e2)½cos e/(cos e-
e)
On passe de P à P' par affinité de rapport a/b. On a a2 + b2 = c2 et e = c/a (excentricité). On en déduit alors que b2/a2 = 1 - e2, puis :
tanj
= tan^(FA,FP) = - tan^(FH,FP) = - HP/HF
= - (HP' × b/a)/(OF
- OH) = (asine
× b/a)/(acose-
ea)
= (b/a).sine/(cose
- e) = (1 - e2)½sine/(cose
- e).

![]() Formule de Gibbs
:
Formule de Gibbs
:
u
∧
(v ∧
w) = <u![]() ,w>
,w>![]() .v
- <u
.v
- <u![]() ,v>
,v>![]() .w
.w
Prouver ce résultat en construisant une base orthonormée judicieuse
Le résultat est trivial si un des vecteurs est nul et très facilement vérifiable si l'un est combinaison linéaire des deux autres.
Lorsque les trois vecteurs sont
linéairement indépendants (ils forment une base de l'espace), posons i
= u/||u||. Dans le plan vectoriel (u,v),
choisissons j normé orthogonal à i et soit k
tel que (i,j,k) soit orthonormée
directe. On peut écrire v = ai
+ bj et w = a'i
+ b'j + c'k. Un petit calcul, utilisant les produits
scalaires et vectoriels des vecteurs de base, montre maintenant facilement que
u
∧
(v ∧
w) et <u![]() ,w>
,w>![]() .v
- <u
.v
- <u![]() ,v>
,v>![]() .w sont
tous deux égaux à ||u||(a'b
- ab')j - ||u||ac'k.
.w sont
tous deux égaux à ||u||(a'b
- ab')j - ||u||ac'k.
➔ Rappel (» produit vectoriel , produit scalaire) :
i
∧
i = j
∧
j = k
∧
k = 0, i
∧
j = k , j
∧
k = i, k
∧
i = j.
Par anticommutativité : j
∧
i = -k , k
∧
j = -i, i
∧
k = -j
i . j = j . k = i, k . i = 0, i . i = j . j = k . k = 1.
![]() Il n'y a que 3 treillis distributifs pour un ensemble de 5
éléments. Mise à part la chaîne, quels sont les deux autres ?
Il n'y a que 3 treillis distributifs pour un ensemble de 5
éléments. Mise à part la chaîne, quels sont les deux autres ?
On n'a guère le choix ! Voici le second :

Le troisième sera obtenu en renversant toutes les flèches.
![]() Dans
un treillis de Boole, le complémenté de tout élément est unique.
Dans
un treillis de Boole, le complémenté de tout élément est unique.
Si x admet deux complémentés y et z, on aura x∧y =
x∧z
= 0 et x∨y = x∨z
= 1. On peut écrire y = y∧1 = y∧(x∨y).
Par distributivité y = (y∧x)∨(y∧z). Mais y∧x = x∧y = 0. donc y = y∧z. En écrivant z = z∧(x∨z),
on aurait de même z = z∧y = y∧z. Donc y = z.
![]() Prouver
que l'ensemble A des automorphismes intérieurs d'un groupe G est un groupe
isomorphe au groupe quotient G/C où C désigne le centre de G.
»
centre d'un magma
Prouver
que l'ensemble A des automorphismes intérieurs d'un groupe G est un groupe
isomorphe au groupe quotient G/C où C désigne le centre de G.
»
centre d'un magma
Soit
* la loi de groupe de G et e son élément neutre. Munissons A de la loi de
composition des applications. A est l'ensemble des Ig : x
→
g*x*g-1, g
∈G. Notons f
l'application qui à tout g de G associe Ig
dans A : f(g) = Ig. On a f(g*g') = Ig*g'.
Or Ig*g'(x) = (g*g')*x*(g*g')-1
= g*(g'*x*g'-1)*g-1
= Ig[Ig'(x)].
Donc Ig*g' = Ig
o Ig'.
Par suite f(g*g') = f(g) o
f(g') et on conclut que f est un homomorphisme de G dans A;
par conséquent A est un groupe isomorphe à
G/N où N est le noyau de f.
On a f(e) = Ie = id
(application identique. Par suite, N = {g∈G
/ f(g) = id } = {g∈G
/ Ig = id }.
Mais Ig
= id
⇔ g*x*g-1
= x pour tout x de G. En composant par , on voit que
N = {g∈G
/ g*x = x*g } pour tout x de G : c'est le centre de G.
![]() Vérifier que l'équation paramétrique x = cosu + v.sinu, y
= sinu - v.cosu, z = v définit un hyperboloïde à une nappe en tant que
surface réglée
pour u et v convenablement choisis. Préciser les génératrices. Trouver une
seconde génération.
Vérifier que l'équation paramétrique x = cosu + v.sinu, y
= sinu - v.cosu, z = v définit un hyperboloïde à une nappe en tant que
surface réglée
pour u et v convenablement choisis. Préciser les génératrices. Trouver une
seconde génération.
x = cosu + v.sinu, y = sinu - v.cosu, z = v. Lorsque v décrit R et u l'intervalle [0,2p], on peut écrire :
j(u,v) = f(u) + v.D(u) = (cosu, sinu, 0) + v.(sinu,-cosu,1)
Il s'agit bien d'une surface réglée s'appuyant sur la courbe u → f(u) = (cosu, sinu, 0), cercle x2 + y2 = 1 dans le plan (xOy). Les génératrices sont, pour chaque valeur de u, les droites d'équation paramétrique x = v.sinu, y = -v.cosu, z = v.
En changeant 1 en - 1 dans D(u) on obtient un vecteur directeur (sinu,-cosu,-1) linéairement indépendant de (sinu,-cosu,1) mais la surface reste manifestement inchangée : elle possède une seconde famille génératrice.
Selon l'équation initiale, on a, en élevant au carré
: x2 + y2 = 1
+ v2 = 1 + z2.
Donc x2 + y2 -
z2 = 1 : il s'agit bien de l'hyperboloïde à une
nappe.
![]() I -
Quelles sont les entiers relatifs qui, divisés par 5 et par 3 donnent
respectivement les restes 1 et 2 ?
I -
Quelles sont les entiers relatifs qui, divisés par 5 et par 3 donnent
respectivement les restes 1 et 2 ?
De tels nombres x existent car 3 et 5 sont premiers entre eux. Selon les hypothèses, il existe des entiers relatifs p et q tels que x = 5p + 1 et x= 3q + 2. On a donc 5p - 3q = 1 (e). Le systèmes est alors équivalent à (e) sous la condition x = 5p + 1 (ou x = 3q + 2). On est ramené à l'identité de Bezout et à la résolution d'une équation du 1er degré à deux variables entières p et q dont la solution générale est p = 3k + 2 et q = 5k + 3. On peut voir que p = 2 et q = 3 fournissent une solution particulière xo = 11. D'où x = 15k + 11 où k décrit Z, c'est à dire x ≡ 11 [15]. » théorème chinois
II - Quels sont les entiers n tels que 4n2 + 1 soient multiples de 5 ?
Le problème se ramène à rechercher n tel que 4n2 + 1 ≡ 0 [5], égalité équivalente à (2n + 1)2 ≡ 4n [5]; or Z/5Z est un corps et si, dans ce corps, a2 = 4b, alors b est un carré, par suite n ≡ 0, 1 ou 4. n = 5k est manifestement à rejeter; les cas n = 5k ± 1 conviennent.
![]() Déterminer les entiers naturels n tels que 52n
+ 5n soit divisible par 13.
Déterminer les entiers naturels n tels que 52n
+ 5n soit divisible par 13.
52 = 25 ≡ -1 [13], donc 54 ≡ 1 [13]. On pourrait chercher n sous la forme 4p + r mais r étant compris entre 0 et 3, ce n'est pas le plus court chemin.
Supposons n pair, n = 2k : 52n = 54k = (54)k ≡ 1 [13] et 5n = 52k = (52)k ≡ (-1)k [13]. L'équation donnée est alors équivalente à 1 + (-1)k ≡ 0 [13] qui est vérifiée si et seulement si k est impair. Donc k est de la forme 2p + 1, p entier, donc n = 4p + 2.
Supposons n impair, n = 2k+1 : 52n = 54k+2 = (54)k × 52 ≡ 1 × (-1) ≡ -1 [13] et 5n = 52k+1 = 5 × (52)k ≡ 5 × (-1)k [13]. L'équation donnée est alors équivalente à -1 + 5 × (-1)k ≡ 0 [13], donc à ±5 ≡ 1 [13], ce qui est clairement inacceptable.
La réponse est donc l'ensemble des entiers congrus à 2 modulo 4, multiples de 4 augmentés de 2. Noter que cet ensemble contient 2 car 0 est multiple de tout nombre (et diviseur d'aucun !).
➔ Une autre voie est de factoriser : 52n + 5n = 5n(5n + 1). Remarquer que les nombres 5n et 5n + 1 étant consécutifs, ils sont premiers entre eux, donc 13 doit diviser 5n ou 5n + 1. On montre alors que 13 ne peut diviser 5n, donc 13 divise 5n + 1 et on est ramené aux calculs précédents de l'alinéa 2.
![]() Déterminer
les solutions du système n∈Z,
n ≡ 13 [19] ,
n ≡ 6 [12].
Déterminer
les solutions du système n∈Z,
n ≡ 13 [19] ,
n ≡ 6 [12].
On rencontre les solutions de cet exercice de bac faisant exclusivement intervenir les congruences au prix de complications inutiles imposées par le sujet. La résolution de systèmes de ce type est pourtant très élémentaire. Par hypothèse, il existe des entiers u et v tels que n = 19u + 13 = 12v + 6. Par différence, on a 12v - 19u = 7.
Or 19 et 12 étant premiers entre eux, on utilise
l'identité
de Bezout fournissant sans difficulté 12 × 8
- 19 × 5 =
1.
Ce qui conduit à u = 35 - 12k et v = 56 - 19k et par suite n = 678 - 228k, ce
qui peut s'écrire n = 222 - 228k, puisque 678 = 222 + 2 × 228
: . Ou encore, quitte à changer k en - k :
(1) n = 228k + 222, k décrivant Z
Mais on n'a pas procédé par équivalence :
inversement si n = 228k +222 = 19 × 12k
+ 222 = 228k +222 = 19 × 12k
+ 19 × 12
- 6. On a donc n
≡
-6
≡
13 [19] et n
≡
-6
≡
6 [12]. Les solutions sont donc effectivement les n tels
que (1).
![]() Sachant
que
a
est à b ce que c est à d signifie
a/b = c/d,
traduire en langage moderne la proposition
XI, livre VII d'Euclide :
Sachant
que
a
est à b ce que c est à d signifie
a/b = c/d,
traduire en langage moderne la proposition
XI, livre VII d'Euclide :
Si le tout est au tout comme le nombre retranché
est au nombre retranché,
le nombre restant sera aussi
au nombre restant comme le
tout est au tout.
 .
Exemple 6/9 = 4/6, donc 2/3 = 6/9.
.
Exemple 6/9 = 4/6, donc 2/3 = 6/9.
![]() On
considère les trois points A, B et C ci-dessous.
Calculer les coordonnées du
point D afin que,
dans cet ordre, ABCD soit un parallélogramme.
Calculer les coordonnées du point D' afin que, dans cet ordre, ABD'C soit un
parallélogramme.
On
considère les trois points A, B et C ci-dessous.
Calculer les coordonnées du
point D afin que,
dans cet ordre, ABCD soit un parallélogramme.
Calculer les coordonnées du point D' afin que, dans cet ordre, ABD'C soit un
parallélogramme.
a/ On a A(1;1), B(4;3) et C(6;2). Dire que ABCD est un parallélogramme revient à écrire AB = DC. On a :
AB (xB - xA;yB - yA), soit : AB(3;2)
Posons D(x;y); on a DC(6 - x;2 - y)
On doit avoir :
6 - x = 3
2 - y = 2
Par conséquent : D(3;0)
b/ nous devons avoir ici AB = CD', ce qui conduit à D'(9;4)

![]() Dans un espace vectoriel
E de dimension 3 sur
R,
rapporté à la base B = (i, j,
k), on considère l'application linéaire f : E →
E
qui à tout vecteur v(x, y, z) associe le vecteur v'(x
- 2y + z, -x - y + 2z, -x + y). Donner la
matrice de f dans la base B.
Dans un espace vectoriel
E de dimension 3 sur
R,
rapporté à la base B = (i, j,
k), on considère l'application linéaire f : E →
E
qui à tout vecteur v(x, y, z) associe le vecteur v'(x
- 2y + z, -x - y + 2z, -x + y). Donner la
matrice de f dans la base B.
Dans la base B, on a i(1, 0, 0), j(0, 1, 0) et k(0, 0, 1). On calcule i' = f(i), j' = f(j) et k' = f(k) et on obtient respectivement i'(1, -2, 1) , j'(-1, -1, 2) et k'(-1, 1, 0). La matrice est alors :

![]() Dans
le cadre de la géométrie "du caoutchouc", il est clair que le polyèdre troué de
droite est homéomorphe au tore :
Dans
le cadre de la géométrie "du caoutchouc", il est clair que le polyèdre troué de
droite est homéomorphe au tore :

Après l'avoir décomposé en polygones ayant deux à deux une arête commune et une seule, dénombrer ses sommets S, ses arêtes A et faces F et montrer que dans ce cas S - A + F = 0 : c'est la caractéristique du tore.
La décomposition ci-dessous en polygones ayant en commun une arête et une seule fournit 16 sommets, 32 arêtes et 16 faces. On a donc S - A + F = 0.

![]() Exercice dans Z/6Z :Déterminer les entiers
naturels n tels que n2 + 2 soit divisible par 6
Exercice dans Z/6Z :Déterminer les entiers
naturels n tels que n2 + 2 soit divisible par 6
N étant inclus dans Z, on peut transposer le problème en termes de congruences en recherchant les entiers n tels que n2 + 2 soit congru à 0 modulo 6. en passant dans Z/6Z, on constate que :
n2 + 2 ≡ 0 [6] ⇔ n2 ≡ 4 [6]
Établissons la table des carrés :
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
x2 |
0 |
1 |
4 |
3 |
4 |
1 |
On déduit de ce tableau que les entiers
n cherchés sont de la forme 6k +2 ou
6k + 4.
Ce qui peut aussi se traduire par n = 6k
± 2.
![]() L'ensemble totalement ordonné (N,≥)
des entiers naturels n'est pas bien ordonné.
On note w* son ordinal.
Montrer qu'une condition
nécessaire et suffisante pour qu'un ensemble ordonné
soit bien ordonné est qu'il ne contienne aucune partie d'ordinal
w*.
L'ensemble totalement ordonné (N,≥)
des entiers naturels n'est pas bien ordonné.
On note w* son ordinal.
Montrer qu'une condition
nécessaire et suffisante pour qu'un ensemble ordonné
soit bien ordonné est qu'il ne contienne aucune partie d'ordinal
w*.
Soit (E,‹) un ensemble ordonné.
la condition est nécessaire :
Si A est une partie de E
d'ordinal w*, alors A n'a pas
de 1er élément : c'est contraire à la définition d'un ensemble bien ordonné.
la condition est suffisante :
nous devons montrer que si
E ne contient aucune partie A d'ordinal
w*, alors il est bien ordonné.
Prouvons la proposition contraposée : Si E est ordonné mais non bien ordonné,
alors E contient une partie d'ordinal
w* :
Par hypothèse, E contient une partie A non vide n'ayant pas de
plus petit élément. Donc si x1 est un élément de A, il existe un x2 de A,
distinct de x1, tel que x2
‹ x1.
Mais x2 ne peut pas être le 1er élément de A. Donc, il existe un x3 de A,
distinct de x2, tel que x3
‹ x2. On
construit ainsi une chaîne infinie ...
‹ x3
‹ x2
‹ x1
dont les éléments constituent une partie de E d'ordinal
w*.
![]() Résoudre dans R les inéquations :
a) | 2x + 3 | > 5
b) | x + 3 |
≤ | 2x
- 3 |
Résoudre dans R les inéquations :
a) | 2x + 3 | > 5
b) | x + 3 |
≤ | 2x
- 3 |
a) Rappelons que sur la droite numérique | A | (valeur absolue de A ) représente la distance de A à O. Par suite :
| 2x + 3 | > 5
⇔ 2x + 3 < -5
ou 2x + 3 > 5
⇔ 2x < -8
ou 2x > 2
Les solutions sont par conséquent les nombres x de l'ensemble ]-∞, -4] ∪ ]1,+∞[.
b) | x + 3 | ≤ | 2x - 3 | : l'inéquation | A(x) | ≤ | B(x) | peut se résoudre par encadrement ou au moyen d'un tableau. Voir par exemple ici un cas résolu. On donne ici la méthode par encadrement :

Si 2x - 3
≥ 0, on a
x ≥ 3/2 :
-2x + 3 ≤
x + 3 ≤ 2x
- 3. La 1ère inégalité fournit x
≥ 0 et la
seconde : x
≥ 6.
On
retient donc x
≥ 6.
Si 2x - 3
≤ 0, on a
x ≤ 3/2 :
2x - 3 ≤ x
+ 3 ≤ -2x
+ 3. La 1ère inégalité fournit x
≤ 6 et la
seconde : x
≤ 0.
On
retient donc x
≤ 0.
Les solutions sont donc les nombres x de l'ensemble ]-∞, 0] ∪ ]6,+∞[.
![]() Résoudre dans R, l'inéquation 2x/|x + 1| < x - 1
Résoudre dans R, l'inéquation 2x/|x + 1| < x - 1
On doit avoir ici x + 1 non nul puisque ce terme est en dénominateur. | x + 1| étant strictement positif, l'équation donnée est équivalente à 2x < | x + 1| (x - 1) et il s'agit de distinguer 2 cas suivant que x + 1 est positif ou négatif.
a/ x + 1 > 0, soit : x > -1. On a alors | x + 1| = x + 1,
l'inéquation devient 2x < x2 - 1, c'est à dire
x2 - 2x - 1 > 0.
On est ramené au
signe du trinôme. Les racines de x2
- 2x - 1 = 0 sont 1 ±
√2, ce
trinôme est strictement positif les intervalles ]-∞,1
-
√2[ et
]1 +
√2,
∞[. Mais nous
avons la condition x > -1; on retiendra par conséquent x∈]-
1, 1 -
√2[∪]1
+
√2,
∞[.
b/ x + 1 < 0, soit : x < -1. On a alors | x + 1| = - x - 1,
l'inéquation devient cette fois x2 + 2x - 1 <
0.
Les racines de x2 + 2x - 1 = 0 sont -1
±
√2, ce
trinôme est strictement négatif sur l'intervalle ]-1
-
√2, -1
+
√2[. Mais
nous avons la condition x < -1; on retiendra par conséquent x∈]-1
-
√2, -1[.
Finalement, les solutions sont éléments de l'ensemble ]-1 - √2, -1[∪]- 1, 1 - √2[∪]1 + √2, ∞[.
Résolution graphique approchée :
L'ordinateur a tracé (en noir) la courbe (c) d'équation y = 2x/| x + 1, en rose la droite d'équation y = x - 1 et, en rouge, la droite d'équation x = -1, asymptote verticale à (c).
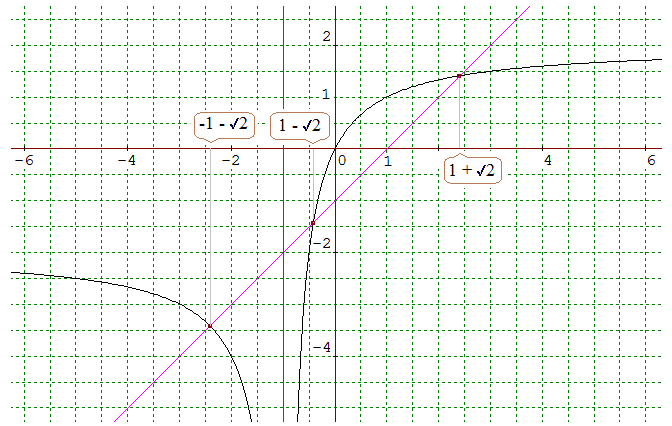
L'ensemble des solutions correspond aux valeurs de x pour
lesquelles la courbe (c) est "en-dessous" de la droite d'équation y = x -
1. On retrouve sensiblement -1 -
√2
≅ -2.4 , 1
-
√2
≅ -0.4 et
1 +
√2
≅ 2.4
![]() Théorème d'Al-Kashi (règle du
cosinus) : a2
= b2 +
c2 - 2bc.cosÂ
Théorème d'Al-Kashi (règle du
cosinus) : a2
= b2 +
c2 - 2bc.cosÂ
(CH) désignant la hauteur issue de C, dans le cas aigu on a CH = b.sin et dans le cas obtus, CH = b.sin(180° - Â) = b.sinÂ. Par application du théorème de Pythagore, on peut écrire : BC2 = BH2 + CH2.
dans le cas aigu : BC2
= a2 = (c - AH)2
+ CH2 = (c - b.cosÂ)2
+ b2.sin2Â.
On développe et on remplace sin2Â par 1 -
cos2Â, ce qui conduit au résultat cherché :
a2
= b2 +
c2 - 2bc.cosÂ.
dans le cas obtus : BC2
= a2 = (c + AH)2
+ CH2 = [c + b.cos(180°-Â)]2
+ b2.sin2Â.
Mais cos(180°-Â = -cosÂ.
Ce qui conduit au même résultat.

![]() Prouver, sans utiliser de théorèmes de convergence que la
série 1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + ... dont on déterminera
sans peine le terme général (il n'y a pas de piège...) est convergente et
préciser sa limite.
Prouver, sans utiliser de théorèmes de convergence que la
série 1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + ... dont on déterminera
sans peine le terme général (il n'y a pas de piège...) est convergente et
préciser sa limite.
Le terme général un peut s'écrire comme l'inverse de n(n + 1) pour tout n de N*. Par décomposition en éléments simples, a/n + b/(n + 1), on obtient a = -b = 1, soit un = 1/n - 1/(n + 1). D'où la somme partielle Sn = (1 - 1/2) + (1/2 - 1/3) + ... (1/n - 1/(n + 1)) = 1 - 1/(n + 1) tend vers 1 : la série converge et sa limite est 1.
En utilisant un théorème de convergence, on notera que l'on a un < 1/n2 : série de Riemann convergente, une référence en la matière !