
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Convergence : absolue , uniforme , normale , conditions & critères | Séries de fonctions, séries entières | Séries de Fourier |
Les notions de suite et de convergence d'une suite sont supposées connues. On pourra également consulter quelques définitions et résultats relatifs aux suites (progressions) arithmétiques et géométriques.
L'étude qui suit traite des séries à valeurs dans E = R ou C mais la plupart des résultats s'adaptent à des espaces métriques (resp. vectoriels normés R ou C) en remplaçant les valeurs absolues ou modules par les distances (resp. normes) correspondantes. Certains critères n'étant alors valables que si de tels espaces sont complets (espaces de Banach).
Soit (un) une suite à valeurs dans un espace F = R, C. On peut sommer, jusqu'à l'infini, les éléments de la suite (un) à partir d'un certain rang : on parle alors de série. L'élément un en sera le terme général. Une série est dite convergente si la suite (Sn) de ses sommes partielles, à savoir :
est convergente vers un point de F. La limite S de Sn est la somme de la série et on convient d'écrire :
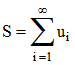
Vu que Sn - Sn-1 = un , si la série converge, alors Sn et Sn-1 ont même limite, donc un tend vers 0 :
Le terme général d'une série convergente tend nécessairement vers 0
Reste de rang n d'une série :
Pour une série de terme général un, que nous noterons dans la suite Σun, posons :
Rn = un+1 + un+2 + un+3 + ...
est appelé reste de rang n de la série Σun. On définit ainsi une suite. On prouvera aisément que :
Une série est convergente si et seulement si son reste Rn converge vers 0.
➔ Si la série converge vers S, alors Rn = S - Sn.
Série divergente :
Une série non convergente est dite divergente. C'est dire que la suite de ses sommes partielles diverge (ne converge pas). La (célèbre) série harmonique 1 + 1/2 + 1/3 + 1/4 + ... , "somme" des inverses de tous les entiers non nuls, en est un exemple. En effet :
![]()
On trouvera la preuve de ce résultat dans le calcul de la constante d'Euler.
∗∗∗
Extrait Bac S, Antilles-Guyane, juin 2005 : »
∗∗∗
1. On considère la série de premier terme u1 =
1, de terme général un = 11111...1 (n chiffres égaux à 1).
Calculer Sn = u1 + u2 + ... + un
Indications :
remarquer que 9Sn = (10 - 1) + (100 - 1) + ...
(10n - 1) = ... Rép. : Sn = 10(10n - 1)/81 - n/9
! Dire qu'une série diverge ne signifie pas que les sommes partielles tendent vers l'infini :
Par exemple, la série de terme général un = (-1)n est divergente. En effet, S2n = 1 et S2n+1 = -1, les sommes partielles reste finies mais ne convergent pas.

!
Lorsqu'une série n'est pas à termes
positifs, regrouper des termes ou modifier leur ordre est illicite !
Cela peut modifier la nature de la série (convergente ou divergente) et sa somme
éventuelle.
• Exemple : la série 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ... diverge. On peut s'en assurer en remarquant que son terme général (-1)n valant 1 ou -1 suivant la parité de n ne tend pas vers 0. On remarque que ses sommes partielles sont alternativement 1 et 0 : la suite des sommes partielles ne converge pas. En regroupant les termes sous la forme (1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + ..., on pourrait croire que la somme existe et est nulle. En écrivant maintenant 1 + (- 1 + 1) + ( - 1 + 1) + ( - 1 + 1) + (- 1 + 1) + ... , la somme serait 1 !!!
Grandi et la série 1 - 1 +1 - 1 + 1 - 1 + ... : »
➔ Une condition suffisante pour autoriser un réarrangement des termes fut prouvé par Dirichlet en 1837, à savoir la convergence en valeur absolue :
Série absolument convergente, série semi-convergente :
Une série Σun sera dite absolument convergente si Σ|un| est convergente (valeur absolue dans le cas réel, module dans le plan complexe). Par opposition, la convergence de Σun est dite simple.
En conséquence très utile dans la pratique, vu que pour tout n, | Σi=o,...,n un | ≤ Σi=o,...,n |un|, on peut énoncer :
Toute série absolument convergente est simplement convergente.
Une série simplement convergente mais non absolument convergente est dite semi-convergente.
Un cas fondamental de série semi-convergente non absolument convergente est la suite harmonique alternée évoquée pour la première fois par Leibniz : 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ... = ln 2.
La série harmonique (exemple de série divergente) : » Séries asymptotiques : »
∗∗∗
2. Prouver, sans utiliser de théorèmes de convergence que la
série 1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + ... dont on
déterminera sans peine le terme général (il n'y a pas de piège...) est
convergente et préciser sa limite. Rép. :
☼
Série commutativement convergente :
φ désignant une permutation de N (bijection de N sur N), une série numérique Σun est dite commutativement convergente pour signifier que Σuφ(n) est également convergente.
Toute série Σun
réelle ou complexe absolument convergente est commutativement convergente
et la série Σuφ(n)
l'est aussi et a même somme.
L'exemple de la série harmonique alternée par réarrangement des termes : »
On peut aussi énoncer :
i/ Dans un espace vectoriel normé complet (» Banach) toute série absolument convergente est commutativement convergente.
ii/ Si φ une permutation de N et Σun une série à termes positifs, alors Σun et Σuφ(n) sont de même nature (toutes deux convergentes ou divergentes) et, si elles convergent, elles ont même somme.
Famille sommable : »
| Conditions de convergence & critères : |
Dans le cas d'une série à termes strictement positifs (tout au moins à partir d'un certain rang), des conditions suffisantes de convergence (théorèmes de comparaison) sont énoncées ci-dessous, mais rappelons tout d'abord un résultat intéressant, conséquence immédiate du théorème selon lequel toute suite croissante majorée de nombres réels est convergente :
Pour qu'une série numérique positive soit convergente il faut et il suffit que la suite Sn
de ses sommes partielles soit majorée.
∗∗∗
3. Appliquer ce dernier résultat à la série
de Riemann de terme général 1/n2 en montrant que la suite des
sommes partielles
est inférieure à 2.- 1/n. Indications :
remarquer 1/n2 < 1/n(n - 1) = 1/(n - 1) - 1/n
☼
1a/ Série majorée :
Si la série Σvn est convergente et si, à partir d'un certain rang p on a un ≤ vn , alors Σun converge
Par exemple : la série de terme général un = 1/n! (n ≥ 0) converge car à partir du rang n = 3, on a un < 1/2n. Or, la série de terme général 1/2n (n ≥ 0) est géométrique de raison 1/2 < 1. Elle converge vers 2. Par suite, la série des un converge et sa somme est inférieure à 3 (on ajoute uo et u1) et supérieure à 2 = uo + u1. C'est le nombre e.
Le nombre e selon Euler : »
➔ A contrario, si la série Σvn est divergente et si, à partir d'un certain rang p on a un ≥ vn , alors Σun diverge.
Par exemple : la série de terme général un = 1/ln(n) (n ≥ 2) est divergente (ln = logarithme népérien) : comparer à la série harmonique.
2/ Séries de même nature :
2a. Si un et vn sont proportionnels (il existe k non nul tel que un = kvn) converge vers un réel non nul, alors les séries Σun et Σvn sont de même nature (toutes deux convergentes ou divergentes).
2b. Si la suite un /vn converge vers un réel non nul, alors les séries Σun et Σvn sont de même nature (toutes deux convergentes ou divergentes).
∗∗∗
4. Un p'tit exo d'application ?
: étude de la série de terme général 2n/(2n-1)k
2c. Si un
et vn sont des infiniment petits équivalents
pour n tendant vers l'infini, alors les séries Σun
et Σvn
sont de même nature (toutes deux
convergentes ou divergentes).
Rappel :
la
condition un
→0 est une
condition nécessaire
de convergence. Dans ces deux cas b et c, on parle de
séries équivalentes.
2d. Soit
Σun
une série à termes positifs; si la suite (un)
décroît à partir d'un certain rang, alors la série Σun
est de même nature que celle de terme général
 où k désigne un
entier naturel au moins égal à 2.
où k désigne un
entier naturel au moins égal à 2.
3/ Règles de d'Alembert :
3a. Si, à partir d'un certain rang, on a un+1 /un ≤ k < 1 alors Σun converge. Si, à partir d'un certain rang, un+1 /un ≥ 1, Σun diverge (c'est le cas si le rapport tend vers 1 par valeurs supérieures).
3b. Si, à partir d'un certain rang, on a un+1/un ≤ vn+1/vn où Σvn est une série convergente, alors Σun converge. Ce résultat conduit au critère de d'Alembert rappelé ci-dessous :
3c. Soit Σun une série à termes strictement positifs pour laquelle le rapport un+1 / un à une limite L. Dans ces conditions :
Le cas L = 1, est litigieux et demande une étude plus approfondie;
le cas un+1 / un décroissant vers 1 est divergent.

La série auxiliaire a pour terme général vn = kne-(n.ln k)². Utilisons le critère de d'Alembert : le rapport vn+1/vn peut s'écrire k/e(ln k)²(2n + 1) tendant vers 0 pour n infini. d'où la convergence de la série des vn et celle des un.
Règle de Duhamel : » Règle de Kummer : »
4/
Règle nαun :
α
désignant un réel positif, si la suite de terme
général nαun converge vers une limite finie non
nulle, alors la série Σun
converge si α > 1, diverge
sinon.
∗∗∗ Exemple d'application de cette règle
➔ Ce résultat est une conséquence de cet important cas particulier :
Les séries, 1 + 1/2p + 1/3p + 1/4p + 1/5p + 1/np + ... dites séries de Riemann, converge pour p > 1, diverge sinon.
Preuve : on regroupe les termes par groupes de 2, 4, 8, 16, ... termes (puissances successives de 2) de la façon suivante :
1 + (1/2p + 1/3p) + (1/4p + 1/5p + 1/6p + 1/7p ) + (1/8p + 1/9p + 1/10p + 1/11p + 1/12p + 1/13p + 1/14p + 1/15p ) + ...
La somme est alors inférieure à :
1 + 2/2p + 4/4p + 8/8p + 16/16p + 32/32p + ... = 1 + 2p-1 + 1/4p-1 + 1/8p-1 + 1/16p-1 + ...
On reconnaît la somme des termes de la progression géométrique (série géométrique) de 1er terme 1, de raison 1/2p-1 qui converge si cette raison est strictement inférieure à 1, donc si p > 1. Remarquer que pour p = 1, on retrouve la série harmonique.
∗∗∗
5. Prouver que la série 1 + 1/32
+ 1/52 + 1/72
+ 1/92 + 1/112
+ 1/132 + 1/152
+... est convergente.
Séries de Riemann et fonction zêta : » Cas des séries alternées (critère de Leibniz) : »
Critères de Cauchy pour les séries :
5a/ La série numérique Σun est convergente si et seulement si pour tout k, k entier : Sn+k - Sn = un+1 + ... + un+k tend vers 0 lorsque n tend vers l'infini (Sn désigne la somme partielle de rang n).
! Dans le cas plus général d'une série à valeurs dans un espace métrique ou vectoriel normé F, le critère se réduit à une condition nécessaire de convergence. La condition devient suffisante si F est complet (F = R ou C ou tout espace vectoriel normé de dimension finie) : » espace métrique , espace de Banach.
» Cas des séries de fonctions | cas des suites : suites de Cauchy
5b/ Un second critère fort utile (enseigné par Cauchy à l'École polytechnique) lorsque le terme général s'apparente à une puissance n-ème dans le cas réel ou complexe :
Soit rn
= |un| (module dans le cas complexe);
si lim (rn)1/n
= λ < 1, alors la série Σun
converge. Si lim (rn)1/n =
λ > 1,
alors la série Σun
diverge. Le cas λ = 1 est litigieux (on
ne peut rien conclure).
➔
Dans le cas d'une série à termes
strictement positifs, si lim
un+1/un (»
règle de d'Alembert)
existe finie ou non, c'est aussi la limite de (un)1/n,
la réciproque étant fausse
(»
suites numériques & exemple).
Voici un contre-exemple :
• soit (un)
définie par un = 2 + (-1)n. On a un = 3 si
n pair et un = 1 si n impair. Suivant que n est pair ou impair,
un+1/un prend alors les valeurs 1/3 et 3 : pas de limite. Mais
(un)1/n vaut 1 si n est impair et 31/n si n
pair et on conclura aisément que (un)1/n converge vers 1.
∗∗∗
6. Vérifier au moyen de ce critère que les séries de terme
général un = e1-n et wn = e-vn
avec vn = (n2+1)/(n+1) sont convergentes.
Rép : on a un
> 0 et (un)1/n = (e1-n)1/n = e(1-n)/n
tendant vers e-1 = 1/e < 1 : la série Σun converge. De
même wn
> 0 et (wn)1/n = e-vn/n;
vn/n = (n2+1)/(n2+n) converge vers 1.
D'où (wn)1/n converge là aussi vers 1/e < 1 : la série
Σwn converge.
6/ Comparaison à une intégrale (critère intégral de Cauchy) :
L'intégrale au sens de Riemann, basée sur la notion de fonction en escalier, conduit à ce résultat fort pratique :
Si un = f(n) est une fonction positive et décroissante de n, alors la série Σun est de même nature que l'intégrale de f sur [0,+∞]. Même résultat si un = f(a + n) et l'intégrale de f sur [a,+∞], a >0.
C'est ainsi que l'on peut prouver la convergence de la série de Riemann de terme général 1/np dont il est fait état ci-dessus.
∗∗∗
7. Utiliser le critère intégral afin de prouver que la série
de terme général un = 1/ln(nn) (n
≥ 2) est
divergente.
Autres exemples d'étude :
Σn!/nn
,
Σ2n/(2n - 1)k ,
développement en série
de atn x ,
autres...
Critère de Dirichlet : » Critère d'Abel : » Autres critères : » Séries de Bertrand : »
| Série produit selon Cauchy ou "produit de Cauchy" : |
Considérons deux séries Σun et Σvn et leurs sommes partielles Un = uo + u1 + u2 + ... + un et Vn = vo + v1 + v2 + ... + vn. Faire le produit des deux séries consiste à sommer tous les produits du type uivj, mais pas n'importe comment car cela peut changer la somme ou la nature de la série (» Dirichlet). Écrivons-les sous forme d'un tableau :
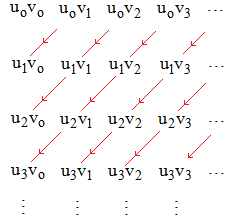
On décide de sommer suivant les diagonales "nord-est → sud-ouest" : elle s'écrit donc :
uovo + (uov1 + u1vo) + (uov2 + u1v1 + u2vo) + (uov3 + u1v2 + u2v1 + u3vo) + ...
C'est ainsi que la série de terme général
wn = Σukvn-k (0 ≤ k ≤ n)
soit :
wn = uovn + u1vn-1 + u2vn-2 + ... + un-1v1 + unvo
est appelée série produit au sens de Cauchy.
Théorème de Cauchy (1821) :
Lorsque les séries sont absolument convergentes, la série-produit l'est aussi et sa somme est le produit des sommes de Σun et Σvn.
Autrement dit :
∗∗∗
Contre exemple de Cauchy
8. Considérer la série de terme général 1 -1/√2
+ 1/√3 - 1/√4
+ 1/√5 - ... et
la série produit par elle-même.
a) Montrer que son terme terme général s'écrit :

b) En utilisant que la moyenne arithmétique (a+b)/2 de deux
nombres positifs a et b est supérieure à leur moyenne géométrique
√(ab),
montrer que la série produit diverge.
»
moyennes arith. et géom.
➔ L'usage des séries produits se rencontre couramment dans le cas des séries de fonctions étudié au paragraphe suivant. Voici, en avant-première..., une application à la fonction exponentielle lorsqu'elle est définie par :
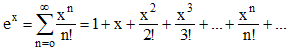
Cette série est clairement absolument convergente (utiliser le critère de d'Alembert) pour tout réel x. Étudions le produit ex x ey : c'est la série-produit de terme général :
![]()
Or n! = k!(n - k)! x Cnk , donc un = (x + y)n/n! : c'est dire que ex x ey = ex + y.
Fonction
exponentielle complexe :
» Transformation d'Abel :
»
| Séries de fonctions, séries entières, convergence simple et uniforme : » cas des suites , convergence normale |
Un exemple fondamental de séries de fonctions est donné par la série de puissances, de terme général xn, dite série géométrique de raison x. Cette série converge pour tout x réel ou complexe de module | x | < 1. En effet, eu égard à la formule que l'on établit facilement par multiplication ou par récurrence, on a :
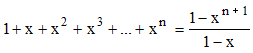
et si x ∈ ]-1,1[, la somme est1/(1 - x) car xn+1 a pour limite 0. Il est licite d'écrire et de retenir :
On parle de série de fonctions car le terme général peut s'écrire fn(x) = xn , image de x par la fonction fn : x → xn. En posant f(x) = 1/(1 - x), tout comme dans le cas des suites, nous dirons que la série de terme général (fn) converge simplement vers la fonction f pour tout x de l'intervalle ]-1,1[, ou encore que f est la limite simple de la série Σfn sur cet intervalle.
➔ Cette série de puissances est un cas particulier de série entière, c'est à dire dont le terme général est de la forme anzn, z et an réels ou complexes.
Rayon de convergence et résultats d'Abel sur les séries entières : » Fonctions entières (analyse complexe) : »
Dans le cas général, lorsque x est élément d'une partie J de R ou C, on dira que la série Σfn admet la fonction f comme limite sur J si la suite des sommes partielles de terme général Sn(x) = fo(x) + f1(x) + f2(x) + ... + fn(x) converge vers f(x) pour tout x de J.
Le reste d'ordre n de la série est le nombre Rn(x) = fn+1(x) + fn+2(x) + fn+3(x) + ... La série Σfn est convergente de somme f sur J, si la suite des Rn(x) converge vers 0 pour tout x de J.
Convergence uniforme :
La convergence d'une série signifie la convergence de la suite de ses sommes partielles Sn(x). On dit alors que la série Σfn converge uniformément sur J, ou que la convergence de la série est uniforme sur J, pour exprimer que la suite Sn(x) = fo(x) + f1(x) + f2(x) + ... + fn(x) converge uniformément. Si f est la somme de la série (limite des Sn), cela revient à exprimer que la suite des restes Rn(x) = f(x) - Sn(x) converge uniformément vers 0 :
Par conséquent :
Σfn converge uniformément vers f sur J ssi la suite Supx∈J | Rn(x)| converge vers 0
Exemple : La série définie sur [0,a], 0 < a < 1, par fn(x) = xn est uniformément convergente, de somme 1/(1 - x). En effet, dans ce cas très simple, on a Sn(x) = 1 + x + ... + xn = (1 - xn+1)/(1 - x) et par conséquent | Rn(x) | = xn+1/(1 - x) et, sur [0,a], on a | Rn(x) | < an+1/(1 - a) du fait de la croissance de x → xn+1/(1 - x) pour tout entier n et vu que 0 < a < 1, la convergence vers 0 de Rn(x) est uniforme.
Remarquer que si [0,1[ remplace [0,a], la série Σfn converge simplement mais ne converge plus uniformément
Contre-exemple : La suite de fonctions définie sur [0,1] par fn(x) = nx/(1 + nx) converge vers 0 si x = 0 et vers 1 pour tout x non nul. Cette convergence n'est pas uniforme : pour x non nul, le reste est Rn(x) = 1/(1 + nx). Il est clair que Rn(x) tend vers 0 mais pour toute valeur de n aussi grande que l'on voudra, on peut choisir un x suffisamment petit de sorte que nx soit encore très petit : Rn(x) serait alors proche de 1 et il faudra donc choisir, pour ce x là, un N "vraiment grand" pour arranger les choses...
Critère de Cauchy pour la convergence uniforme d'une série de fonctions :
La formulation du critère de Cauchy pour les séries numériques s'adapte aux séries de fonctions à valeurs dans R ou C :
La série de
fonctions Σfn
converge uniformément vers f sur J si et seulement si
pour tout k, k entier
et tout x de J : |Sn+k(x) -
Sn(x)| = |un+1(x) + ... + un+k(x)|
tend vers 0 lorsque n tend vers l'infini.
! Dans le cas plus général d'une série à valeurs dans un espace métrique ou vectoriel normé F, le critère se réduit à une condition nécessaire de convergence. La condition devient suffisante si F est complet (F = R ou C ou tout espace vectoriel normé de dimension finie) : » espace métrique , espace de Banach.
» Cauchy
Critère de Weierstrass pour la convergence uniforme d'une série de fonctions :
Soit fn(x)
le terme général d'une série de fonctions numériques et un celui d'une série numérique positive convergente.
Si, à partir d'un certain rang, on a |fn(x)|
≤ un pour tout x
d'un intervalle fermé J,
alors la série des fn converge uniformément sur J.
La série de terme général fn(x) = xn/n!, de somme partielle Sn = 1 + x/1! + x2/2! + x3/3! + ... + xn/n!, est uniformément convergente sur tout intervalle J = [a,b] car |fn(x)| ≤ |b|n/n! pour tout x de J et la série de terme général positif un = |b|n/n! est convergente; on s'en convaincra en appliquant le critère de d'Alembert : un+1/un = b/(n + 1) < 1 dès que n ≥ b. On a reconnu là le développement en série de la fonction exponentielle x → ex.
Convergence uniforme et continuité :
Si fn(x) est le terme général d'une série uniformément convergente sur J et si (toutes) les fn sont continues en un point xo de J (resp. sur J), alors la somme f de la série est continue en xo (resp. sur J).
Convergence uniforme et intégration "terme à terme" :
Si fn(x) est le terme général d'une série numérique réelle uniformément convergente sur un intervalle [a,b] et si les fn sont continues sur [a,b], alors :
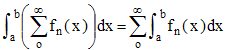 (intégration
terme à terme)
(intégration
terme à terme)Autrement dit, en notant f est la somme de la série, l'intégrale de la somme est la somme des intégrales :
Convergence uniforme et dérivation "terme à terme" :
Les conditions sont plus subtiles :
si Σfn(x) est une série de fonctions numériques continûment dérivables (les fn sont dérivables et les dérivées sont continues) sur un intervalle [a,b]; si la série Σfn converge en (au moins) un point xo de [a,b] et si la série Σf 'n des dérivées est uniformément convergente sur [a,b], alors la série des fn est uniformément convergente sur [a,b] et :
![]() (dérivation terme à terme)
(dérivation terme à terme)
» En notant f ' la somme de la série des dérivées, on peut aussi exprimer que la dérivée de la somme est la somme des dérivées :
Calcul de 1/9801, une application de ce résultat à une division très spéciale : »
| Convergence normale d'une série de fonctions : » convergence uniforme |
Une convergence plus forte que la converge uniforme est la convergence normale :
Une série de fonctions réelles ou complexes Σfn est dite normalement convergente sur J, s'il existe une série Sun convergente à termes positifs pour laquelle on a pour tous n de N et z de J : |fn(z)| ≤ un.
Toute série de fonctions normalement convergentes réelles ou complexes et plus généralement à valeurs dans un espace vectoriel normé complet (espace de Banach) est uniformément convergente.
➔
Ce qui est normale relève d'une norme, alors pourquoi ce qualificatif de normale ? dans le cas où la série des fn(z) est à valeurs dans un espace vectoriel normé F, la norme || || remplace la valeur absolue (resp. le module) qui est la norme usuelle de R (resp. C) considéré comme espace vectoriel sur lui-même. Restreignons-nous alors aux séries de fonctions bornées de J dans F. Pour de telles fonctions f, le nombre (( f )) = Supz∈J ||f(z)|| est fini et est une norme dans leur ensemble, dite norme de la convergence uniforme.• Si la série des fn converge normalement, il existe une série Σun convergente à termes positifs telle que ||fn(z)|| ≤ un pour tout n et z. On a donc (( fn )) ≤ un et la série des (( fn )) converge donc en vertu du critère 1a. Inversement, si la série Σ(( fn )) converge, en posant un = (( fn )), on a ||fn(z)|| ≤ un pour tout n et z. La série des fn converge donc normalement.
En conséquence :
Dans l'ensemble des fonctions bornées de J vers F, la convergence normale d'une série de fonctions fn équivaut ici à la convergence de la série des normes (( fn )) généralement notées || fn ||∞.
Topologie et norme de la convergence uniforme : » Convergence normale et calcul de π : »
➔ Pour en savoir plus :
Tout traité d'analyse niveau DEUG sciences. On peut citer :
Mathématiques générales, algèbre-analyse, Ch. Pisot & M. Zamansky. Ed. dunod, Paris, 1956.
Des MathÉmatiques pour les Sciences,
par Caude Aslangul (univ. Paris 6). Concepts, méthodes et techniques pour
la
modélisation.
Éd. De Boeck - Bruxelles, 2011.
Cours de mathématiques,
Tome 2, Jacqueline Lelong-Ferrand, Jean-Marie Arnaudiès
Classes préparatoires, 1er cycle universitaire - Dunod
Université - 1978 (4 volumes)
Mathématiques L2 Cours complet avec 700 tests et exercices corrigés
ouvrage collectif
sous la direction de Jean-Pierre Marco.
Éd. Pearson Education - Paris, 2007