
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 Savant
éclectique,
Brook Taylor s'adonna à la musique, à la peinture et à la
philosophie. Il fut formé aux mathématiques par John
Machin et compléta ses études à l'université de Cambridge.
Savant
éclectique,
Brook Taylor s'adonna à la musique, à la peinture et à la
philosophie. Il fut formé aux mathématiques par John
Machin et compléta ses études à l'université de Cambridge.
Admirateur de Newton, dont il adopta les idées et perfectionna sa méthode des fluxions, Taylor fut membre de la Royal Society de Londres (l'équivalent de notre Académie des sciences) dès 1712 (il n'a que 27 ans). Il en fut le secrétaire en 1714.
En dehors de certains travaux en géométrie axés sur la perspective qui servira de base à la photogrammétrie, on lui doit principalement la publication (1715-1717) de son traité sur le développement en série des fonctions : Methodus incrementorum directa et inversa, qui engendra injustement des disputes de paternité car il fut le premier à établir de tels développements dans le cas général et non pour une fonction particulière.
La photogrammétrie (IGN, Belgique) : »
| Formule de Taylor : » cas complexe , cas de plusieurs variables |
La célèbre formule est en fait l'aboutissement de travaux entamés auparavant par Gregory,
Newton,
Leibniz
et Jacques
Bernoulli. Selon
CDSB, en 1712, dans une lettre à son ancien maître, John
Machin, Taylor écrit que sa formule est née du
problème de Kepler concernant le calcul de l'anomalie excentrique d'une
planète :
Si f est une fonction de classe Cn dans un voisinage V du
réel a (i.e. admettant des dérivées
continues jusqu'à l'ordre n) et si
f(n) est dérivable sur V (existence de la
dérivée n+1-ème de f sur V) alors :
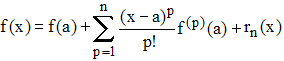 , c'est à
dire :
, c'est à
dire :
![]()
Le calcul (ou la majoration) du reste rn et par là, les conditions de convergence, n'est pas étudié rigoureusement par Taylor.
Contre-exemple de Cauchy :
Un exemple de développement de Taylor convergent, mais non vers la fonction initiale, fut donné par Cauchy au moyen de la fonction f : x →e-1/x² avec la valeur de continuité f(0) = 0. Les dérivées de f sont le produit par e-1/x² de polynômes en 1/x. En posant u = 1/x au voisinage de 0, lorsque x tend vers 0, u tend vers l'infini avec le signe de x, ce qui ramène l'expression des dérivées de f au moyen de termes de la forme uke-u², termes tendant vers 0 dans tous les cas, l'exponentielle l'emportant sur la puissance :
Par exemple, lorsque x tend vers 0+,
u = 1/x → +∞
: f '(x) = e-1/x² × 2/x3
= 2e-u² × u3
= 2u3/eu² < 2u3/eu
→ 0. Et de
même, par imparité, en 0-.
De même, f ''(x) = e-1/x² × (-6/x4
+ 4/x6)
→ 0 et on peut poser
f ''(x) = 0.
Finalement, f : x →e-1/x², pourtant non constante au voisinage de 0, admet un développement "nul"... Pour ce type de fonction prolongée par continuité, ainsi que ses dérivées, un développement de Taylor ou de Maclaurin peut s'avérer inadapté !
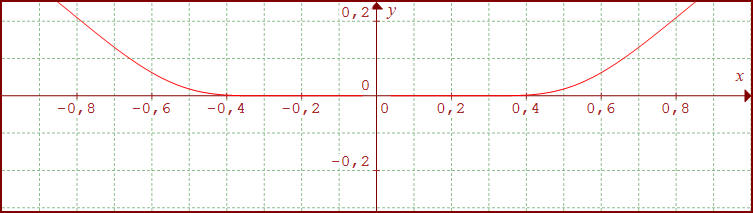
Il est vrai qu'au voisinage de 0, la fonction
e-1/x² est un peu aplatie...
C'est pourquoi, suite à des travaux ultérieurs, le développement de Taylor fut partiellement rebaptisé : formule de Taylor-Lagrange, Taylor-Young, Taylor-Laplace :
Reste de
Lagrange (1797, très pratique) :
Si f est de classe Cn+1 sur V, alors il existe un réel c de V tel
que :
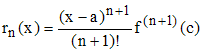
Un exemple classique : le développement en série de la fonction exponentielle ex au voisinage de zéro avec reste de Lagrange :
La fonction factorielle (n!) l'emporte sur la puissance : c'est dire que le reste rn(x) tend vers 0 pour tout x et par conséquent :
Calculs de e : »
où ε est une fonction définie dans un voisinage de a et vérifiant lim x →o ε(x) = o.
| Formule de Taylor & développement limité : |
Les formules de Taylor et de Maclaurin sont les outils privilégiés pour obtenir le développement limité d'une fonction sur un intervalle. Rappelons que f est dite posséder un développement limité à l'ordre n dans un voisinage V de zéro, si pour tout x de V, on peut écrire :
f(x) = ao + a1x + a2x2 + ... + anxn + xnε(x)
avec lim ε(x) = 0 lorsque x tend vers 0
Ce ne sont pas les seuls moyens comme le montre l'exemple suivant : on sait que (1 + x + x2 + ... + xn)(1 - x) = 1 - xn+1. D'où :
Par conséquent, 1 + x +
x2 + ... + xn est le développement
limité à l'ordre n de la fonction
![]() au voisinage de 0.
au voisinage de 0.
Les développements limités sont utilisés pour l'approximation polynomiale des fonctions, l'étude des limites à l'infini (comportement asymptotique) ou en un point de discontinuité, ainsi que le comportement local, comme la position de la courbe représentative par rapport à sa tangente.
➔ Au moyen des notations de Landau, on écrit aussi plus simplement o(xn) au lieu de xnε(x) pour signifier un reste dont le quotient par xn tend vers 0. Par exemple, dans le développement ci-dessus, au voisinage de x = 0, on peut écrire :
1/(1 - x) = 1 + x + x2 + x3 + o(x3)
car on est assuré que le reste x4 + x5 + ... admet x3 en facteur d'une quantité dont la limite en 0 est nulle.
➔ Plus généralement la fonction f est dite posséder un développement limité à l'ordre n en un point xo si, dans un voisinage de xo, on peut écrire :
f(x) = ao + a1(x - xo) + a2(x - xo)2 + ... + an(x - xo)n + (x - xo)nε(x)
avec lim ε(x) = 0 lorsque x tend vers xo
| Formule de Taylor dans le cas de plusieurs variables, point critique, condition d'extremum : |
Sans être insoluble, le problème est un peu plus compliqué... Le cas de 2 variables étudié ici se généralise cependant : en posant x = a + h, y = b + k, h et k "petits", il s'agit de développer f(a + h, b + k). Posons pour cela x = a + ht, y = b + kt, t désignant un paramètre indépendant de x et de y. On définit alors une fonction g de la variable t :
g(t) = f(x,y) = f(a + ht, b + kt),
On remarque que g(0) = f(a,b) et on peut appliquer la formule de Maclaurin à g(1) = f(a + h, b + k) :
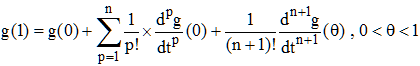
On exprime les dérivées d'ordre p, dpg/dtp, en utilisant la formule de différenciation d'ordre p de la fonction de deux variables g(t) = f(a + ht, b + kt) en remarquant que dx = h.dt et dy = k.dt :
dpg(t)/dtp = (∂/∂x × dx + ∂/∂y × dy)(p)f /dtp = (h.∂/∂x + k.∂/∂y)(p)f /dtp
Donc :
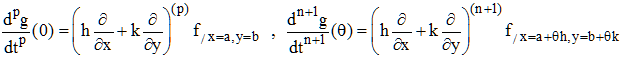
D'où la formule de Taylor pour deux variables : » convention d'écriture
∗∗∗
Donner le développement de Taylor d'ordre 2 au
point (1,1) lorsque f(x,y) = x3y2
- x2y + 2x + 1
☼
Contrôler votre développement en calculant f(1,01;1,01),
soit h = k = 1/100.
Condition d'extremum, point critique, col, selle :
Posons Δf = f(a + h, b + k) - f(a,b). Pour h et k suffisamment petits, Δf sera du signe du 1er terme du développement, de degré 1 en h et k. C'est dire que si ce premier terme n'est pas identiquement nul, la fonction f ne peut admettre au point (a,b) un maximum ou un minimum. Plus généralement, on peut énoncer :
f désignant une fonction numérique définie sur un ouvert U de Rn admettant au moins des dérivées continues d'ordre 1, une condition nécessaire d'extremum en un point a = (a1, a2, ... , an) est ∂f/∂x1 = ∂f/∂x2 = ... = ∂f/∂xn = 0 au point a. Un tel point a est appelé point critique de f.
Dans le cas de deux variables, en considérant la surface z = f(x,y), ∂f/∂x = ∂f/∂x = 0 signifie que le plan tangent en a est horizontal. f admet un maximum (resp. minimum) signifie alors que les points de la surface se situent en dessous (resp. au-dessus) de ce plan tangent, Δf ayant au voisinage de a le signe du terme du second ordre dans le développement de Taylor : Δf > 0 en cas de minimum, Δf > 0 en cas de maximum.
Lorsque Δf ne conserve pas un signe constant au voisinage de a, les points de la surface se situent de part et d'autre du plan tangent : on parle de col ou de point selle.
Extrema dans le cas de deux variables : » Extrema et déterminant de Hesse : »
Indicatrice de Dupin : »
➔ Pour en savoir plus :
Cours de mathématiques,
Tome 2, par Jean Bass, Éd. Masson et Cie - Paris, 1964.
Sur la formule de Taylor par
Marcel Brelot, Annales de l'université de Grenoble,
sur le site Numdam
:
http://archive.numdam.org/article/AUG_1945__21__91_0.pdf