ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Structure de groupe
∗∗∗
Exemples et exercices tout au long de la page et
ici »
Autres structures» Sous-groupe | Sous-groupe distingué | Action de groupe, groupe opérant sur un ensemble | Orbite | groupe à opérateurs Groupes finis | Groupe Z/nZ | Groupe quotient, groupe résoluble | Groupes libres | Soustraction & division |
Un groupe G est un ensemble muni d'une opération (loi de composition interne), notée ici T, qui à tout couple (x,y) de G associe un élément, noté xTy, de G pour laquelle les axiomes suivants sont vérifiés :
g1/ la loi T est associative : (xTy)Tz = xT(yTz) pour tout x, y et z de G
g2/ la loi T possède un élément neutre n : xTn = nTx = x pour tout x de G
g3/ tout élément x de G possède un symétrique x' pour la loi T : xTx' = x'Tx = n
Le groupe G muni de sa loi T est souvent noté (G,T).
➔ L'appellation groupe est de Galois, la structure est de Cauchy, l'axiomatisation de Cayley. Le terme fut sans doute choisi pour signifier un ensemble dont les éléments sont unis par des propriétés opératoires remarquables.
➔ Dans un groupe (G,T) tout élément x est régulier (simplifiable) :
xTa = xTb ⇒ a = b (simplification à gauche) et xTa = xTb ⇒ a = b (simplification à droite) » preuve
Groupe commutatif ou abélien :
Un groupe est dit abélien (du nom de Abel) ou commutatif si sa loi de composition est commutative : xTy = yTx pour tout x et tout y de G.
Loi de composition interne & magma : » Homomorphisme : »
Si A(R) désigne l'ensemble des fonctions affines bijectives de R sur R : fonctions de la forme x → ax + b avec a non nul, (A(R), o) est un groupe non commutatif (o : loi de composition des applications). Si f désigne x → 2x - 1 et si g désigne x → 3x , on a : f o g : x → 6x - 1 et g o f : x → 6x - 3.
Si Ao(R) est le sous-ensemble de A(R) constitué des fonctions x → ax (b = 0), alors (Ao(R), o) est un groupe commutatif, sous-groupe de A(R).
|
∗∗∗ |
|
|
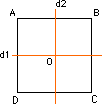
1. Dans un plan P, soit ABCD un carré de centre O,. So la symétrie centrale par rapport à O, S1 la symétrie d'axe d1 passant par les milieux de [AD] et [BC], S2 la symétrie d'axe d2 passant par les milieux de [AB] et [CD] et i l'application identique de P. Montrer que muni de la loi de composition des applications, l'ensemble : E = {i,So,S1,S2} est un groupe commutatif dont on dressera la table de Pythagore. ☼ 2. Soit (E,∗) un groupe d'élément neutre e dans lequel tout élément est involutif (c.à.d. x ∗ x = e). Prouver que ce groupe est commutatif. |
 |
Groupe additif et groupe multiplicatif :
Un groupe dont la loi de composition est commutative (groupe abélien) et possédant des caractéristiques semblables à celle de l'addition dans Z est dit additif et sa loi est notée + si cela n'entraine pas d'ambiguïté contextuelle. à l'instar de Z, dans un tel groupe, l'élément neutre, qualifié d'élément nul, est souvent noté 0 et un symétrique est qualifié d'opposé.
Un groupe dont la loi
de composition possède des
caractéristiques semblables à celle de la
multiplication dans R* = R -{0}, corps des nombres réels, ou celle de
Q* = Q -{0}, corps des fractions de Z, est dit multiplicatif
et sa loi est notée × si cela
n'entraine pas d'ambiguïté contextuelle. Dans un tel groupe, l'élément neutre
est souvent noté 1 (ou I matrice unité
neutre pour le produit matriciel, id : application
identique, neutre pour la loi de
composition des applications) et qualifié d'élément
unité. Un symétrique est qualifié d'inverse.
Il faut bien reconnaitre que ces dénominations sont floues et abusives, ce qui est contraire à l'essence, à l'esprit et à la déontologie mathématique... Mais elles ont le tort ou le mérite de se rencontrer dans la littérature et il fallait donc tenter de les définir !
En fait, on les rencontre dans la théorie des structures algébriques possédant plus d'une loi de composition (anneaux et corps, espaces vectoriels, algèbres), ce qui permet de distinguer de manière concise la loi de composition à laquelle on se réfère.
Conventionnellement, on dit que :
la loi de groupe d'un anneau est son addition, la seconde loi est sa multiplication
! Opposé et inverse :
Au collège (et au lycée...), on confond parfois (souvent ?) inverse et opposé :
l'opposé est le symétrique pour l'addition; l'opposé de 4 est - 4 car 4 + (- 4) = 0.
l'inverse est le symétrique pour la multiplication; l'inverse de 4 est 0,25 car 4 × 0,25 = 1.
l'inverse de n (non nul) pour la multiplication n'est autre que 1/n; l'inverse de 4 est 1/4 = 1 ÷ 4 = 0,25.
l'inverse de n a même signe que n; l'inverse de -12/0,6 est -0,05; en effet -12/0,6 = -120/6 = -20; l'inverse est donc -1/20 = - 0,05.
Groupe additif & Soustraction, groupe multiplicatif et division :
Depuis l'école primaire, on connaît bien la soustraction des entiers naturels, voire la division. On peut certes les qualifier d'opération mais ce ne sont généralement pas des lois de composition interne car leurs résultats n'appartiennent généralement pas à l'ensemble de nombres utilisés
La soustraction n'est pas une loi de composition interne dans N : par exemple, 2 - 3 n'est pas un entier naturel; elle en est une dans Z, ensemble des entiers relatifs. La division n'est pas une loi interne dans N* : par exemple, 2 ÷ 3 n'est pas un entier naturel, mais elle en est une dans Q*, ensemble des nombres rationnels (de la forme a/b, a et b entiers relatifs). En effet, a/b ÷ c/d = ad/bc∈Q*.
Dans les exemples ci-dessus, on constate que soustraction et division sont des lois internes à condition de se placer dans un groupe :
♦ Dans un groupe additif (G,+), tout élément admet un symétrique, généralement appelé opposé. On nomme soustraction, la loi de composition interne qui à tout (x,y) de G × G associe l'élément z = x + y' de G où y' désigne l'opposé de y dans G. Cet opposé étant généralement noté -y, on écrit z = x - y.
!
La soustraction
n'est pas commutative,
tout à l'opposé..., elle anticommutative
: y - x = - (x - y).
» le
produit
vectoriel est également anticommutatif.
•
La soustraction n'est pas
associative : (x - y) - z est distinct de x - (y - z) = (x - y) + z ; cette
non associativité est une importante source d'erreurs au collège qui ne se
tarit pas totalement au lycée. De même dans le cas de la division...
Exemple : (8
-
4) - 2 = 4 - 2 = 2 mais 8
- (4
- 2) = 8 -
2 = 6.
• L'élément nul 0 de (G,+), neutre pour son
addition n'est pas neutre pour la soustraction : x - 0 = x mais 0 - x = - x,
opposé de x. O n'est donc qu'un élément neutre à droite.
♦ Dans un groupe multiplicatif (G,×), tout élément admet un symétrique, généralement appelé inverse. On nomme division, la loi de composition interne qui à tout (x,y) de G×G associe l'élément z = x × y' de G où y' désigne l'inverse de y dans G.
Cet inverse étant généralement noté 1/y, on notera z = x × 1/y ou plus simplement z = x/y "x sur y"). A l'école primaire, on utilise aussi x ÷ y (" divisé par y), notation d'ailleurs souvent pratique. Plus rarement, on utilise x : y : ambigüe et peu convaincante.
!
La division n'est pas commutative,
tout à l'inverse..., , : y/x est l'inverse de x/y.
La division n'est pas associative
: (x ÷
y) ÷ z
est distinct de x ÷
(y ÷ z)
= (x ÷
y) × z
et comme pour la soustraction, cette non associativité est une
importante source d'erreurs au collège et au lycée.
Exemple : (8
÷
4) ÷ 2 = 2 ÷ 2 = 2 mais 8
÷ (4
÷ 2) = 8 ÷
2 = 4.
L'élément unité 1 de (G, ×),
neutre pour sa multiplication n'est pas neutre pour la division : x
÷ 1 = x mais 1
÷ x = 1/x inverse de x. 1 n'est donc qu'un élément
neutre à droite.
Opérations sur les fractions #1 et 2 : » Opérations sur les fractions #3, le piège des écritures : »
| Semi-groupe, demi-groupe ou encore monoïde : |
On appelle parfois ainsi un magma dont la loi est associative et unifère. Une telle structure peut être symétrisée (d'où son appellation). On demande parfois que la loi soit commutative ou encore que tout élément soit régulier.
En savoir plus : »
| Sous-groupe : |
On nomme ainsi une partie S d'un groupe (G,∗) qui, muni de la loi de G, est aussi un groupe. Pour qu'il en soit ainsi, il faut et il suffit que :
a/ le composé x∗y de deux éléments de S soit élément de S : on dit que S est stable pour la loi ∗.
b/ le symétrique x' dans G de tout élément x de S soit aussi élément de S.
➔ Noter que cette définition entraîne implicitement l'appartenance à S de l'élément neutre e de G en utilisant l'existence du symétrique (selon b/) et l'appartenance du composé x ∗ x' (selon a/) fournissant e.
Un résultat pratique :
(S,∗) est un sous-groupe de (G,∗) d'élément neutre e si et seulement si e
∈
Preuve : très simple, la preuve de ce résultat est un bon exercice.
∗∗∗
2. Soit n∈N
et nZ = {nx, x∈Z}.
Montrer que nZ est un sous-groupe additif de Z.
Rép. :
☼
3. Dans le groupe (C,×)
des nombres complexes, l'ensemble des nombres de module 1 est un sous-groupe
de C.
4. Dans le groupe (F,+) des fonction
numériques, l'ensemble des fonctions linéaires x
→ ax est un sous-groupe de
F.
Dans (M2,×),
groupe multiplicatif des matrices carrées réelles inversibles d'ordre 2, on
considère l'ensemble L des matrices du type
Montrer que (L,×) est un sous-groupe
commutatif de (M2,×).
»
lien analogique sur
Wikipedia
: Transformation de Lorentz
dans le cadre de la relativité restreinte
!
Dans (R*, × ),
soit F = [½,2]. Montrer que l'inverse de tout élément de F
est élément de F.
(F,×)
est-il cependant un sous-groupe de (R*,×)
?
Théorème 2 :
Tout sous groupe de (R,+) est de la
forme αZ (α∈R) ou bien est dense dans R
(comme par exemple le sous-groupe additif (Q,+) des nombres rationnels).
Preuve : on pourra se référer au devoir corrigé de Matthieu Romagny, UPMC : » réf. 10.
Théorème 3 :
Toute intersection, finie ou non, de sous-groupes d'un groupe G est un sous-groupe de G.
C'est une conséquence immédiate du théorème 1.
|
Sous-groupe engendré par une partie d'un groupe : |
Soit (G,∗) un groupe fini ou non et A une partie de G finie ou non. L'intersection ‹A› de tous les sous-groupes de G contenant A est un sous-groupe de G contenant A et c'est le plus petit sous-groupe de G contenant A (» E. H. Moore). On dit que ‹A› est le sous-groupe engendré par A. Les éléments de A constituent un système générateur ou une base de ‹A›.
! Un système générateur n'est en général pas unique. Penser à Z pouvant être engendré par {1} ou {1}. Le groupe (G,∗) lui-même est engendré par lui-même mais aussi par G - {e} s'il n'est pas réduit à son élément neutre !
On appelle rang d'un groupe le plus petit cardinal (au sens de l'inclusion) des parties qui le génèrent.
Théorème 4 :
le sous-groupe engendré par A est l'ensemble des composés d'un nombre fini d'éléments de A et de leurs inverses.
Preuve : notons H l'ensemble des composés d'un nombre fini d'éléments de A et de leurs inverses. On a H⊂‹A› et en vertu du théorème 1, H est un sous-groupe de G. Par définition de ‹A›, on a aussi H⊂‹A›, donc H = ‹A›.
Groupe monogène, groupe cyclique :
Dans un groupe (G,∗) d'élément neutre e et non réduit à {e}, on considère un élément a distinct de e dont on note a' le symétrique. Posons :
H = {..., a'(n) , ..., a'(3) , a'(2) , a', e , a, a(2), a(3) , ... , a(n), ...}
en désignant par a(n) le composé de n éléments égaux à a avec la convention a(o) = e, a(1) = a. Notation semblable concernant a'. Dans le cas multiplicatif, on note simplement an et, dans le cas additif, na. Tout élément de H admet son symétrique dans H : [a(n)]' = a'(n) et [a'(n)]' = a(n).
(H,∗) est un sous-groupe commutatif de (G,∗) : on parle de groupe monogène (racine grecque : engendré par un seul). On dit aussi que H est engendré par a et on peut le noter simplement ‹a›.
Un sous-groupe monogène peut être fini : on parle de groupe cyclique. Cela se produit, s'il existe un entier p non nul pour lequel a(p) = e et le plus petit entier non nul vérifiant cette égalité est alors l'ordre du groupe. Il est bien clair que :
Théorème 5 :
Tout groupe monogène (donc tout groupe cyclique) est commutatif.
Le groupe additif (Z,+) des entiers relatifs est monogène (engendré par 1 ou -1) mais il est infini : non cyclique.
Dans (Q,×), l'ensemble des puissances entières d'un nombre non nul a est un groupe multiplicatif monogène infini, isomorphe au groupe additif (Z,+) vu l'égalité am+n = am × an. Considérer par exemple l'ensemble des puissances de 2.
Dans le groupe multiplicatif (R-{0},×), l'ensemble H = {10n, n∈Z} des puissances de 10 est un sous-groupe monogène.
Le groupe additif Z/nZ des classes résiduelles modulo n est engendré par la classe de 1. C'est un groupe fini d'ordre n : groupe cyclique.
Dans C, les racines n-èmes de l'unité munies de la multiplication constituent un groupe cyclique. Le cas des racines 4èmes est intéressant : {1, i , -1 , -i} est engendré par i ou bien -i.
Groupes fondamentaux finis ou non : » Groupes libres : »
|
Sous-groupe normal (ou distingué) d'un groupe : |
C'est Evariste Galois qui introduisit cette structure, également appelée sous-groupe distingué : un sous-groupe H d'un groupe (G,∗) est ainsi dénommé si pour tout x de G et pour tout h de H, le produit x∗h∗x-1 est élément de H.
Étude de la notion de sous-groupe distingué : » Sous-groupes conjugués : »
|
Torsion d'un groupe, groupe de torsion : |
Un élément d'un groupe G, d'élément neutre e, est dit d'ordre fini s'il existe un entier n de N tel que g(n) = e, la notation g(n) désignant comme ci-dessus le composé de n éléments égaux à g.
On appelle torsion du groupe l'ensemble Tor(G) des éléments d'ordre fini de de G.
On dit que G est un groupe de torsion s'il coïncide avec sa torsion : G = Tor(G). Tout groupe fini, comme Z/nZ est un groupe de torsion.
∗∗∗
a/ Vérifier que si le groupe G est abélien
(commutatif), alors Tor(G) est un sous-groupe de G.
b/ Montrer que le groupe quotient Q/Z est un groupe de torsion
infini, sous-groupe de torsion de R/Z.
Groupe quotient d'un groupe par un de ses sous-groupes distingués : »
| Groupe quotient : |
Lorsque H est un sous-groupe de (G,∗), la relation définie dans G par x ~ y ssi x∗y'∈H, y' désignant le symétrique de y, est une relation d'équivalence (vérifiez-le !). L'ensemble quotient (ensemble des classes d'équivalence) G/H, muni de la loi induite par G, est un groupe (commutatif si G l'est).
Dans l'étude d'un groupe abstrait, l'existence et l'étude d'un groupe quotient ayant (beaucoup) "moins" d'éléments permet d'étudier plus aisément le groupe G par le biais de H et G/H. Dans le cas arithmétique des classes résiduelles modulo n, on passe d'un infinité d'éléments à n éléments !
Le concept de groupe quotient permet la construction du groupe (Z,+) des entiers relatifs par symétrisation ainsi que celle du groupe multiplicatif (Q*,×) des nombres rationnels (fractions) non nuls.
Étude et exemples de structures quotients : »
| Groupe opérant sur un ensemble (action de groupe) : |
Introduction :
Lorsque (K, +, ×) est un corps commutatif d'élément unité noté 1, sa multiplication (a,b) →a × b confère à K-{0} la structure de groupe multiplicatif et si E un espace vectoriel sur K, la loi externe de E (multiplication scalaire), notée ici ♦ , vérifie a ♦ (b ♦ x) = (a × b) ♦ x ainsi que 1 ♦ x = x pour tous a et b de K et tout x de E.
On dit que K est un domaine d'opérateurs et les propriétés ci-dessus expriment que le groupe K-{0} des scalaires non nuls opère (ou agit) sur E. On dit aussi que la multiplication scalaire de E est une action du groupe K-{0} sur E.
Cas général :
Plus généralement, E désignant un ensemble non vide, on dit qu'un groupe (G,∗), d'élément neutre e, opère (ou agit) sur E, pour exprimer qu'il existe une application de G × E dans E, s'interprétant comme une loi de composition externe dans E, qui à tout a de G et tout x de E associe l'élément de E noté ici a ♦ x, vérifiant pour tout b de G :
1. a
♦
(b
♦
x)
=
(a∗b)
♦
x (associativité
mixte)
2. e
♦
x = x
On parle d'action du groupe G sur l'ensemble E. On dit aussi que G est un groupe d'opérateurs sur E.
Stabilisateur :
Avec les notations précédentes, (G,∗) opérant sur E de loi externe ♦ , soit x un élément de E. Le sous-ensemble des éléments a de G tels que a ♦ x = x est un sous-groupe de G appelé stabilisateur de x.
Groupe opérant fidèlement :
Avec les notations précédentes, (G,∗) opérant sur E, (a,b)∈G × G, on dit que G opère fidèlement lorsque a ♦ x = b ♦ x pour tout x de E n'a lieu que si a = b.
Théorème 6 :
G opère fidèlement sur E si et seulement si son élément neutre e est
l'unique élément tel que e
♦
x = x pour tout x de E.
Autrement dit : ∀ x
∈ E, a
♦
x = x
⇒ a = e
(et inversement, selon 2)
Preuve : i/ Supposons a
♦ x = b
♦ x
⇒ a
= b et que a
♦ x = x pour
tout x de E.
Soit a' le symétrique de a dans G. On a d'une part a'
♦ (a
♦ x) = a
♦ x et d'autre
part, selon 2, a'
♦ (a
♦ x) = (a'∗a)
♦ x = e
♦ x. C'est dire
que pour tout x, on a a
♦ x = e
♦ x, d'où, par
hypothèse a = e.
ii/ Supposons a
♦ x = x
⇒ a = e
et que a
♦ x = b
♦ x.
Selon 2, en désignant par b' le symétrique de b
dans G, on a successivement : (b'∗a)
♦ x =
b'
♦ (a
♦ x) =
b'
♦ (b
♦ x) = (b'∗b)
♦ x = e
♦ x = x.
On a donc (b'∗a)
♦ x = x,
ce qui implique (par hypothèse) b'∗a
= e : par conséquent, en composant cette égalité à gauche par b dans G,
on a l'égalité cherchée a = b.
|
Orbite (ou trajectoire) d'un élément, groupe opérant transitivement : |
Avec les notations précédentes, (G,∗) opérant sur E, soit x un élément de E. Soit R la relation binaire définie dans E par :
x R y ⇔ il existe a dans G tel que y = a ♦ x
Selon 2 , R est réflexive. Si y = a ♦ x, soit a' le symétrique de a dans G, selon 1 , on peut écrire a' ♦ (a ♦ x) = (a'∗a) ♦ x, c'est à dire a' ♦ y = x : la relation R est symétrique. Supposons enfin y = a ♦ x et z = b ♦ y. On a alors, encore selon 1 : z = b ♦ (a ♦ x) = (b∗a) ♦ x. La relation R est transitive. Il s'agit donc d'une relation d'équivalence.
L'orbite (ou la trajectoire) de x dans E est sa classe d'équivalence x = {y∈E, y = a ♦ x, ∀a∈G}. Les orbites forment ainsi une partition de l'ensemble E.
E désignant l'ensemble des vecteurs du plan (ou tout autre espace vectoriel réel de dimension 2) identifié à R2, considérons le groupe (H, o) des homothéties vectorielles h de E (du type v → kv, k réel) agissant sur E par (h,v) → h ♦ v = h(v). Soit u un vecteur non nul de E. L'orbite de u est l'ensemble des vecteurs colinéaires à u, c'est à dire la droite vectorielle engendrée par u.
E désignant ici le plan (resp. l'espace) euclidien identifié à R2 (resp. R3), considérons le groupe des isométries affines f de E laissant O invariant, sous-groupe de Iso(E), agissant sur E par (f,M) → f ♦ M = f(M). L'orbite M d'un point M de E est l'ensemble des points N de E tels que N = f(M), f décrivant Iso(E). Vu que f(O) = O, N = f(M) ⇔ ON = φf(OM) où φf est l'isométrie vectorielle associée à f. Par suite M = {N∈E / ||ON|| = ||OM||}, orbite s'identifiant dans R2 (resp. R3) au cercle (resp. à la sphère) de centre O, de rayon OM.
Le groupe G est dit opérer transitivement lorsque, pour tout x de E, l'application φx : G → E, φx(a) = a ♦ x est surjective. Autrement dit, l'orbite de tout x n'est autre que E. Si, de surcroit, φxest bijective pour tout x de E, on dira que G agit simplement transitivement.
Groupe à opérateurs :
On parle de groupe à opérateurs pour qualifier un groupe (G,∗) muni d'une action T : E × G → G distributive par rapport à la loi de groupe :
Pour tout k de E (ensemble des opérateurs) et tout (a,b) de G2 : k T (a∗b) = (k T a)∗(k T b)
Dans tout groupe commutatif (G,∗), d'élément neutre e, l'action "n-ème itéré", (n,x) → nTx = x(n) est définie par la relation de récurrence :
n∈N, x(o) = ε et x(n+1) = x ∗ x(n)
E est ici N. Cette action est distributive par rapport à la loi ∗ : (x ∗ y)n =xn ∗ yn. Dans le cas additif, par exemple dans (Z,+) : x(n) = x + x + ... + x est simplement noté nx et n(x + y) = nx + ny; on retrouve la distributivité de la multiplication sur l'addition. Dans le cas multiplicatif, par exemple dans (Q,×), nous aurions nTa = a(n) = a × a × ... × a est simplement noté an, puissance n-ème de a, et kT(a ∗ b) = (kTa) ∗ (kTb) s'écrirait (a x b)n = an x bn : la puissance n-ème d'un produit est le produit des puissances n-èmes.
∗∗∗
Vérifier que l'on peut généraliser l'action
précédente à n∈Z
en posant x-1 = x', x' désignant le symétrique de x pour la loi de
groupe
|
Groupe opérant simplement transitivement et construction formelle d'un espace affine : |
Soit V un espace vectoriel sur un corps commutatif K et ε un ensemble non vide dont les éléments, appelés points, sont notés ici au moyen de lettres majuscules (afin de "coller" à la notion élémentaires du plan et de l'espace de la géométrie euclidienne). Les éléments de V (vecteurs) sont notés en minuscules gras italique : u, v, OM, AB, etc. Le vecteur nul, élément neutre de (V,+) est noté 0. La définition abstraite qui suit est basée sur la notion intuitive de translation rencontrée élémentairement dès le collège en géométrie plane.
Définition :
On dit que ε est un espace affine associé (ou attaché) à l'espace vectoriel V s'il existe une action du groupe additif (V,+) sur ε, loi de composition externe V × ε→ε, notée provisoirement T, opérant simplement transitivement sur ε.
Les relations de définition du groupe (V,+) agissant sur ε s'écrivent ici :
Pour tout u et v de V et tout M de ε : uT(vTM) = (u + v)TM
Pour tout M de ε : 0 TM = M
Dire que (V,+) agit simplement transitivement signifie que pour tout point M de ε, les applications φM : V → ε, φM(v) = v T M sont bijectives :
Quel que soit le couple de points (M,N) de ε × ε, il existe un unique vecteur v de V tel que v T M = N
On dira que N est le translaté de M dans la translation de vecteur v et on pose conventionnellement v = MN.
En particulier, étant donné un point O dans ε, pour tout point M de ε, il existe un unique vecteur v de V que φO(v) = M. On dit que O est un point origine de ε. Avec la notation vectorielle précédente, on a alors : φO(v) = M ⇔ v = OM.
La correspondance M→OM qui à tout point M associe le vecteur OM est donc une une application bijective de ε sur V, ce qui permet d'identifier le couple (ε,O) à l'espace vectoriel E et on convient d'écrire N = v T M = v + M ou encore : ON = v + OM.
Le couple (T,v) s'interprète comme la translation de vecteur v notée tv. Les relations 1. et 2. de définition s'écrivent maintenant :
Pour tout M de ε : tu(tv(M) = tu + v(M), soit, de manière fonctionnelle : tu o tv = tu + v.
t0(M) = M.
N.B. Les conventions d'écriture v = MN et ON = v + OM, conduisent à MN = ON - OM.
Notion élémentaire d'espace affines, applications affines, transformations affines élémentaires : »
|
Groupe opérant simplement transitivement et preuve du théorème de Cayley : |
Théorème 7 :
Tout groupe fini d'ordre n est isomorphe à
un sous-groupe du groupe symétrique Sn
pour mémoire, Sn est de cardinal n!
(factorielle n)
Lemme :
Soit (B,o) le groupe des bijections de E muni de la loi de composition des applications. Le groupe (G,∗), d'élément neutre e, opère sur E si et seulement s'il existe un homomorphisme de G sur B, c'est à dire une application Φ de G sur B tel que Φ(a∗b) = Φ(a) o Φ(b).
Preuve :
i/ Si (G,∗), d'élément neutre e,
opère sur E au moyen de la loi
♦, soit g
∈G. Posons pour tout
x de E, φg(x) = g
♦ x. On définit
ainsi une application φg de E dans E. Pour tous a et b de G, on a φa*b(x)
= (a∗b)
♦ x et, par
distributivité mixte : φa*b(x) = a
♦ (b
♦ x) = a
♦ φb(x)
= φa(φb(x)) = (φa o
φb)(x). Si on note
A l'ensemble
des applications de E dans lui-même, l'application Φ : g
→ φg
vérifie donc φa*b = (φa
o
φb) : homomorphisme de (G,∗)
dans (A,o).
Montrons maintenant que les φg sont bijectives : pour tout g de G,
notons g' son inverse pour la loi ∗de
G. Pour tout x de E, on a φg
o
φg' (x) = φg'*g(x) = φe(x) = g
♦ x = x. Donc φg
o
φg' = φg'*g(x) = idE. Selon
fonctions, théorème2,
φg
est bijective et (φg)-1 = φg'
: φg est donc une bijection de E. Ce qu'il fallait démontrer.
ii/ Inversement, supposons qu'il existe un homomorphisme de G sur
B, c'est à dire
une application Φ de G sur B
tel que Φ(a∗b) = Φ(a)
o Φ(b). Définissons la loi externe de E par Φ(g)(x) = g
♦ x. On a : a ♦
(b
♦ x) =
Φ(a)(Φ(b)(x)) = (Φ(a) o
Φ(b))(x) = Φ(a∗b)
♦ x = (a∗b)
♦ x. Enfin,
e
♦ x = Φ(e)(x) =
idE(x) = x car dans un homomorphisme de
groupe, l'image de l'élément neutre de départ est l'élément neutre du groupe
image.
Ce lemme permet de prouver le théorème de Cayley :
Preuve :
il suffit de choisir le cas particulier E = G. Dans ce
cas, pour tout x de G, φg(x) = g
♦ x = g∗x.
L'homomorphisme Φ : g
→ φg
est injectif, est donc bijectif de G sur le sous-groupe Φ(G). G étant de
cardinal fini, il en est de même de Φ(G) isomorphe à G. Les bijections φg
(appelées translations à gauche par identification aux translations g + x
du cas additif) sont des permutations de G. D'où le résultat.
Par exemple : reprenons le cas de cet exercice. Posons F = {1,2,3,4}. Il y a 4! = 24 permutations des éléments de F constituant S4. Identifions A, B, C, D à 1, 2, 3, 4. On vérifiera que les 4 symétries i, So, S1 et S2 étudiées s'identifient respectivement à id : (1,2,3,4) → (1,2,3,4), p1 : (1,2,3,4) → (3,4,1,2), p2 : (1,2,3,4) → (4,3,2,1), p3 :(1,2,3,4) → (2,1,4,3) et que ces permutations involutives constituent un sous-groupe commutatif d'ordre 4 de S4.
Les groupes finis et le groupe symétrique Sn : » Groupe de Lie (groupe topologique) : »
∗∗∗
Les exercices suivants sont indépendants
1.
Montrer que dans (Z,∗) avec a∗b = |a - b| , 0 est
neutre et tout élément est son propre et unique symétrique.
(Z,∗) est-il un
groupe ?
2. On considère sur l'intervalle réel J = [1,+∞[, le magma (J,*) défini par :
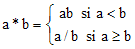
Montrer que 1 est neutre dans (J,*) et que tout élément
est son propre et unique symétrique. (J,*) est-il un groupe ?
3. Montrer que le magma (N,∗) défini par :
est associatif et unifère. (N,∗) est-il un groupe ?
4. Montrer qu'un magma associatif (J,∗) admettant un élément neutre à droite (resp. à gauche) et dans lequel tout élément possède un symétrique à droite (resp. à gauche) est un groupe.
6. Dans un groupe abélien (G,T), appelons loi inverse de T, la loi notée ⊥ définie dans G par : a ⊥ b = aTb' où b' désigne le symétrique de b dans (G,T).
➔ Pour en savoir plus :