ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 VIETE François,
français, 1540-1603 |
Natif
de Fontenay le Comte (Vendée), François
Viète étudia le droit à l'université de Poitiers. C'est ainsi qu'il fut un avocat
renommé auprès de cours princières européennes, puis conseiller, dès 1571, au parlement de
Paris (cour de justice) sous Henri
III et Henri IV.
Viète, de par sa passion pour l'astronomie, découvre les mathématiques. C'est ainsi qu'il développera la trigonométrie plane et sphérique en usant du système décimal. Selon certains historiens, il aurait perçu avant Kepler la nature elliptique des orbites planétaires dans son Harmonicon Coeleste, écrit vers 1597, mais ce traité est hélas perdu.
Son traité d'algèbre (In Artem Analyticam Isagoge, 1591) est d'une remarquable modernité. En tant que conseiller, sa notoriété s'accrut par ses capacités à déchiffrer les codes secrets des puissances étrangères, en particulier lors de la guerre entre la France et l'Espagne. Notoriété qui lui valut des accusations de sorcellerie... En géométrie, on lui doit de nombreuses publications relatives aux coniques, aux problèmes de construction hérités de l'antiquité comme celui de la trisection de l'angle, de la quadrature du cercle et principalement ceux d'Apollonius (Apollonius Gallus, 1600), dont le problème des trois cercles, disponibles (en latin) sur le site Gallica de la BnF :
Ces problèmes de construction sont fort intéressants et certains, quitte à choisir des cas particuliers, sont accessibles au niveau collège et lycée. On trouvera à la page Apollonius de Perge, le descriptif de ces problèmes et des renvois en pages d'exercices corrigés.
| L'apport du système décimal positionnel : |
Dans un important ouvrage, Canon mathematicus, seu ad triangula cum appendicibus, publié à Paris en 1579 et commencé en 1571, Viète développe la trigonométrie plane et sphérique, et, dans un addendum, tend à imposer le calcul décimal au détriment du système sexagésimal (base 60) en usage depuis l'Antiquité :
"En mathématiques les soixantièmes et les soixantaines (c'est à dire la base 60 qu'utilisèrent les mathématiciens babyloniens puis grecs) doivent être d’un usage rare ou nul. Au contraire les millièmes et les mille, les centièmes et les centaines, les dixièmes et les dizaines doivent être d’un usage fréquent ou constant". Source : Mathématiques et mathématiciens, J. Itaard & P. Dedron, 1972.
Canon Mathematicus sur Gallica (en latin) : » Les systèmes de numération : »
➔ L'écriture actuelle n,dcm... d'un nombre décimal, préconisée par Viète, distinguant les parties entière et décimale (d=dixièmes, c=centièmes, m=millièmes,...) est sans doute antérieure et due à l'astronome hollandais Snellius. Viète utilisa une écriture proche en collant la partie fractionnaire à la partie entière comme dans :
L'œuvre principale de Viète sera In Artem Analyticam Isagoge (1591), publié à Tours, premier grand traité d'algèbre symbolique. Viète est considéré, en France, comme étant à l'origine du calcul algébrique "moderne". Il écrit encore en latin, à la façon de Bombelli, mais en utilisant les signes opératoires actuels + et - pour la somme et la différence, hérités de l'allemand Widmann, ce qui allège sensiblement la lecture.
Dans une équation, les consonnes (resp. les voyelles) sont les paramètres connus (resp. les inconnues). Il utilisa le terme actuel de coefficient dans une équation. Un demi-siècle plus tard, Descartes adoptera cet usage qui se répandra dans toute l'Europe.
Précision :
On note généralement D l'ensemble des nombres décimaux, c'est à dire l'ensemble des nombres admettant un représentant de la forme x = a × 10n avec (a,n)∈Z2. C'est dire que l'écriture de x est limité : ses décimales sont nulles à partir d'un certain rang
1,675 = 1675 × 10-2 est décimal;
2 774 563 000 (deux milliards sept cent soixante quatorze millions cinq cent soixante trois mille) est décimal, on peut l'écrire 2 774 563 × 103.
5/13 = 0,38461538461538461538... n'est pas décimal : son écriture décimale est illimité et périodique de "période" 461538. On parle de nombre rationnel (fraction) non décimal.
» Stifel
3/8 = 0,375 est décimal. On peut tout aussi bien l'écrire 0,375000000000.... mais c'est inutilement compliqué... : à partir des dix-millièmes, ses décimales sont toutes nulles, on ne les écrit donc pas (on parle parfois à l'école et au collège de décimales inutiles).
le nombre π = 3,14159265359... possède une infinité de décimales non nulles et non périodiques. Cette absence de périodicité montre que π n'est pas rationnel : ce n'est pas une fraction.
➔ Pour qu'une fraction irréductible a/b non nulle soit le représentant d'un nombre décimal, il faut et il suffit que les seuls diviseurs premiers de b soient 2 ou 5 (le "ou" n'étant pas exclusif).
7/8 est décimal car 8 = 23; de même 39/150 = 13/50 car 50 = 2 × 52.
379/150 n'est pas décimal : cette fraction est irréductible et 150 = 2 × 3 × 52 ne vérifie pas la condition énoncée.
On remarquera que (D,+,×) est un anneau unitaire intègre, sous anneau de (Q, +,×). Ce n'est pas un corps : 3 est décimal mais non pas son inverse 1/3.
| Les équations ax2 + bx = c et x3+ ax = b |
Viète résolut complètement l'équation du second degré ax2 + bx = c. Il affirma pouvoir ramener les problèmes de son époque à la résolution d'équations et émet, à juste titre, la conjecture selon laquelle la trisection de l'angle est liée à l'équation du 3è degré qu'il résolut dans sa forme x3 + ax = b lorsque a et b sont des nombres positifs.
Les racines négatives d'une équation sont considérées comme fausses et il évite toute discussion sur le sujet ! Mais les racines imaginaires sont déjà "inventées" grâce au génie de Bombelli et Viète sera aussi l'un des premiers à pressentir, suivi par Girard et Descartes, le théorème fondamental de l'algèbre que d'Alembert puis Gauss démontreront.
| Relations (ou fonctions) symétriques des racines : |
Viète remarque, tout comme Harriot, les relations, dites parfois aujourd'hui de Viète, existant entre les solutions et les coefficients d'une équation algébrique : en ramenant à 1 le coefficient du terme de plus haut degré, notons x1, x2, ..., xn les solutions (éventuellement multiples). On a :
x1 + x2 = -p
x1x2 = q
x1 + x2 + x3 = -p
x1x2 + x2x3 + x3x1 = q
x1x2x3 = -r
☼ Par exemple, pour l'équation
du 3ème degré : x3 + 3x2 - 2x - 6
= 0, en notant simplement a, b et c les racines (réelles ou
complexes), on aura : a + b + c =
-3 , ab + ac + bc =
-2 , abc = 6
x1 +
x2 + ... + xn =
-an-1
x1x2
+ x1x3 + ... + xn-1xn
= an-2
(somme de
tous les produits 2 à 2)
x1x2x3
+ x1x2x4 + ... +
xn-2xn-1xn =
-an-3 (somme de tous les
produits 3 à 3)
...
x1x2...xk
+ x1x2...xk+1+ ... +
xn-kxn--k+1...xn =
(-1)kan-k (somme
de tous les produits k à k)
...
x1x2...xn
= (-1)nao.
➔ Les racines peuvent être éventuellement multiples et sont ici considérées réelles ou complexes.
Ces relations seront étudiées par Girard et Descartes, puis Lagrange et Cauchy, lesquels perçoivent leur rôle dans la résolution générale des équations algébriques. Mais ce sera Galois qui montrera au 19è siècle, au moyen de la théorie (naissante) des groupes finis, que les équations de degré supérieur à 4 ne sont généralement pas résolubles par radicaux (i.e. les solutions ne peuvent s'exprimer au moyen de combinaisons de racines carrées, cubiques, ..., n-èmes des coefficients).
∗∗∗
1°/ En application de ces formules, montrer que deux équations algébriques de même degré ont les mêmes racines si
et seulement si leurs
coefficients sont proportionnels (l'un étant nul, l'autre
devra aussi l'être).
2°/ Pour quelles valeurs de m l'équation x4 - 6x3 + mx2 - 11x + 6 = 0 a-t-elle
deux racines de somme 2 ?
| La trigonométrie et le calcul de π : |
Viète précise et développe la trigonométrie de Regiomontanus et donne, ce qui est tout à fait impressionnant pour l'époque (1593), une expression de π sous la forme d'un produit infini d'irrationnels simples :
∗∗∗
On note un le terme général de ce produit
infini contenant n radicaux. En particulier u1 = 2/√2
= √2. Exprimer un
en fonction de un-1.
Justifier que cette suite est croissante,
majorée par 2. En déduire sa convergence et calculer sa limite.
» prolongement
: exercice niveau sup/spé
Suite croissante majorée ou décroissante minorée : »
| Formule de Viète ou théorème de Pythagore généralisé ou encore théorème d'Al Kashi : |
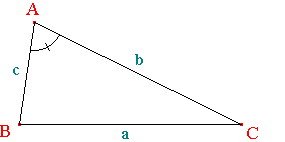Viète étudia aussi la résolution des
triangles et la formule, dite
de
Viète, généralisant
le théorème de Pythagore
pour un triangle ABC dont les côtés mesurent a, b et c,
remonte en fait à des temps plus anciens. On la doit en effet
au mathématicien arabe Al
Kashi :
➔ Notons cependant que sous une forme purement géométrique, avec l'introduction d'une hauteur convenable, ce résultat était déjà présent au livre II des Éléments d'Euclide :
Stevin