ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 PYTHAGORE de Samos,
grec,
-560?/-480?
exercices :
série 1, série 2 |
Astronome, philosophe, musicologue, ce célèbre savant, disciple de Thalès,
nous est connu par ses disciples et successeurs, les
Pythagoriciens (également dits Pythagoréens ou Pythagoristes).
Aucun écrit ne nous est parvenu. Pour plus d'objectivité, on doit se fier principalement aux historiens de l'Antiquité tels Hérodote, Proclus, Diogène Laërce. Personnage mythique (il laisse se propager la rumeur selon laquelle il serait le fils d'Apollon), Pythagore créa son école à Crotone, laquelle devint rapidement une secte aux règles de vie très sévères. Devenant alors dérangeant, persona non grata, il mourra assassiné dans des conditions obscures, certains historiens avançant l'incendie de son école.
Notes et gamme musicale :
On attribue à Pythagore, en son école, l'origine du terme
mathématiques au sens grec de
mathematikos = celui qui veut apprendre (scientifiquement), forgé sur
mathêma = ce qui est enseigné, la connaissance.
Pythagore est le premier théoricien de la technique des nombres, en un mot : l'arithmétique, sur laquelle il fonda sa philosophie : l'harmonie du Monde est régie par les nombres entiers, le pair, l'impair et la décade : la dizaine.
Les Pythagoriciens annoncent là une rupture avec le système sexagésimal des Chaldéens dont l'usage se perpétuera cependant en astronomie.
| Cosmogonie : |
Selon certains auteurs (
ci-après), Pythagore, ou plus certainement ses
disciples de l'école de Crotone, auraient affirmé la
sphéricité de la Terre tournant, ainsi que les autres
astres (soleil compris), autour d'un feu central invisible (Hestia = le Foyer).
Cette vision pyrocentrique de l'univers fut en fait introduite par Philolaos de Crotone, philosophe et disciple direct de Pythagore, et annonce la théorie héliocentrique (le Soleil est au centre de notre système planétaire) hélas mise à l'écart par Eudoxe et Aristote. Bien que défendue par le grand astronome Aristarque un siècle et demi plus tard, le non moins célèbre Ptolémée prôna le géocentrisme (la Terre est au centre de l'Univers, le Soleil tourne autour) et plongea le monde dans l'erreur pendant 2000 ans jusqu'à l'entrée en scène de Galilée et de Copernic.
Pythagore et les Pythagoriciens (que
sais-je n° 2732) de J.-F.- Mattei (1993) :
"Nous pouvons admirer cet étrange système de Philolaos qui eut peu
de succès en son temps et dont les trois hardiesses prophétiques attendront 2000
ans avant de se réaliser : 1) la Terre et tous les astres sont sphériques 2) la
Terre est un corps céleste de second plan 3) la Terre n'est pas en repos et
n'occupe pas le centre du monde, comme ce sera le cas chez Platon et Aristote."
Nouveau Larousse illustré en 7 volumes (1906, sous la dir. de Paul Augé), vol.
1, au titre Astronomie :
"Pythagore enseignait les deux mouvements de
la Terre sur elle-même et autour du Soleil; il avait des vues élevées
sur les systèmes planétaires mais elles manquaient de preuve, et leur vérité
fut complètement méconnue."
Dictionnaire Hachette encyclopédique
(1997) :
"il entrevit le mouvement de la
Terre sur elle-même et enseigna qu'elle était sphérique".
Astronomie moderne de R. Tocquet,
préface de Louis Leprince-Ringuet (1965) :
"(...) il est difficile
de préciser parmi les doctrines pythagoriciennes, celles qui appartiennent en
propre au Maître? Quoi qu'il en soit, les
Pythagoriciens enseignaient que la Terre et le Soleil sont sphériques, que le
Soleil décrit sur la sphère céleste un grand cercle, l'écliptique, dont le plan
est incliné sur celui de l'équateur et il y a tout lieu de penser qu'ils
enseignaient également que les planètes et les comètes tournent autour du
Soleil."
Pythagore et les Pythagoriciens (que
sais-je n° 2732) de J.-F.- Mattei (1993) :
"Pythagore
enseignait la sphéricité de la Terre et du Monde non pour des raisons
empiriques (comme les contours de l'ombre durant les éclipses) mais pour des
raisons théoriques d'ordre harmonique, le plus beau des solides étant la sphère." :
Pythagore parlait de la musique des sphères (les astres) que nous
n'entendions pas car notre oreille, trop habituée, ne parvenait pas à les
discerner...
|
Le célèbre théorème de Pythagore et les relations métriques dans le triangle rectangle : |
Il affirme que dans un triangle
ABC rectangle en A, le carré du côté qui
sous-tend l'angle droit
(hypoténuse)
est égal à la somme des carrés des deux autres
côtés :
cliquer sur la tablette pour l'agrandir
Ce
résultat, que Pythagore ne semble pas avoir prouvé, est en fait antérieur au
célèbre philosophe : on le retrouve 2000 ans avant J.-C. dans une tablette
babylonienne cunéiforme (Plimpton 322,
Université de Columbia, New York, USA).
Réciproquement :
Si, dans un triangle ABC, le carré d'un côté est égal à la somme des carrés des deux autres, alors ce triangle est rectangle (en le sommet opposé au plus grand côté qui est alors son hypoténuse).
Le plus beau triangle de l'histoire des mathématiques est,
sans conteste, le triangle de côtés 3, 4 et 5 : il est rectangle et est parfois nommé
triangle d'or mais cette appellation est plutôt réservée à
ceci... Pour ce triangle 3,
4, 5, on parle plutôt de triangle égyptien :
Le triangle égyptien
Voûte égyptienne :
Les démonstrations du célèbre théorème, et de sa réciproque, sont présentes dans les Eléments d'Euclide et font l'objet des deux dernières propositions 47 et 48, du livre I. Selon certains auteurs, Pythagore aurait sacrifié, pour fêter sa découverte, entre 1 boeuf et tout un troupeau de 100 bœufs (soit une hécatombe, du grec hékaton = cent et boûs = boeuf) selon une tradition festive et religieuse de l'époque. Curieux cependant pour une secte végétarienne dont Pythagore était le gourou...
1. Le triangle ABC est rectangle en C. AB = 20
et BC = 10. Calculer AC. Rép :
10
3
2. Le triangle isocèle en A vérifiant AB = 9,99 et BC = 14,14 est-il rectangle ?
Rép : non.
on ne dira pas qu'il est presque
rectangle ou qu'il est rectangle à 0,01 près !!! Il n'est pas rectangle. Point
!..
3. Le triangle ABC vérifie BC = 7 cm, AC = 6 cm et
ACB = 31°. Construire avec soin ce triangle. Est-il rectangle ?
Rép : non car si ABC est rectangle, on doit avoir cos31° = 6/7,
or...
| Autres relations métriques dans le triangle rectangle : |
De cette relation fondamentale découle d'autres égalités fort
utiles, dites relations métriques dans le triangle rectangle comme (H désignant
le pied de la hauteur issue de l'angle droit) :
AB2 = BH x BC
Preuves : la première relation (donc aussi la seconde) peut être exprimée au moyen de la propriété de Thalès en remarquant que les triangles rectangles ABC et ABH sont semblables (mêmes mesures d'angles), donc quitte à modifier la figure en remplaçant ABH par AB'A' (ci-dessus) afin d'obtenir une configuration de Thalès avec AB' = BH et (B'A')//(BC), on a :
AB'/AB = B'A'/BC, soit BH/AB = AB/BC, soit AB2 = BH x BC.
La troisième relation indiquée AH x BC = AB x AC, est évidente si on la considère en tant qu'égalité d'aires : ABC est un triangle d'aire (AH x BC)/2 mais aussi la "moitié d'un rectangle d'aire (AB x AC)/2.
La quatrième relation s'obtient en élevant au carré la 3ème et en utilisant la 1ère et la seconde pour remplacer AB2 et AB2. La dernière est conséquence de AH x BC = AB x AC : réduire au même dénominateur le membre de droite, utiliser ensuite que AB2 + AC2 = BC2...
Théorème de la médiane dû à Apollonius de Perge :
Collégiens :
un seul h à
hypoténuse! Ne pas confondre avec hypothèse
qui a deux h... : du grec hypothesis
avec un sens étymologique proche, il est vrai :
hypoténuse : du grec hupo = sous et teinein = tendre : côté qui sous-tend l'angle droit.
hypothèse : du grec hupo = sous et theînai = poser , thesis = action de poser, dans le sens d'un propos que l'on place à la base de son discours et sur lequel on développe sa pensée (thèse).
Une
preuve élémentaire utilisant les aires se comprend aisément par
la figure de gauche : on considère un carré de
côté a + b; on prouve facilement que le
quadrilatère intérieur (en vert) est un carré de
côté noté c. Dans ces conditions :
Cette preuve n'est pas sans rappeler celle du mathématicien indien Bhaskara:
selon Euclide :
selon Bhaskara
:
|
Rue Jeanne et Darc aire élémentaire, théorème de Pythagore |
|
Calcul d'aire par différence cercles tangents, losange, théorème de Pythagore |
| Cinq cercles inscrits dans un carrés facile |
| Pyramide de disques assez facile |
| Pyramide de boules plus subtil.. |
| Cube inscrit mesure du côté du cube inscrit dans une sphère |
| Ligne d'horizon théorème de Pythagore |
| Le triangle égyptien unique triangle rectangle de mesures consécutives |
|
Relations métriques dans le triangle rectangle en conséquence de la propriété de Thalès |
| Divisibilité et premiers résultats sur les nombres premiers : |
Outre une claire distinction
entre le pair (forme 2
n) et
l'impair (forme 2n+1),
on doit aux Pythagoriciens
d'importants résultats d'arithmétique sur :
les nombres premiers (n'ayant pas de diviseurs autres que 1 et eux-mêmes) qu'Euclide étudiera tout particulièrement dans ses Éléments;
la notion de nombre parfait : entier égal à la somme de ses diviseurs autres que lui-même. Ces nombres sont "rares" et intriguent encore de nos jours les mathématiciens. En deçà de 10000, il n'y en a que 4 :
6 , 28 , 496 , 8128
On ne sait toujours pas aujourd'hui s'il existe des nombres parfaits impairs. Euclide établit que ces nombres sont de la forme 2n-1(2n - 1) avec la condition 2n - 1 est premier : nombre de Mersenne.
En savoir plus sur les nombres parfaits :
Nicomaque et les nombres polygonaux :
|
Triplets pythagoriciens ou triades : |
Les triplets (a,b,c) d'entiers naturels non nuls, tels que a2 + b2 = c2 , comme (3,4,5), furent étudiés par Euclide (encore lui !) et Diophante, lequel fut le premier grand spécialiste des équations en nombres entiers. Il en existe une infinité que l'on peut caractériser facilement ou calculer au moyen de l'ordinateur. Les Pythagoriciens trouvèrent ceux de la forme :
a = 2n + 1 , b = 2n2 + 2n , c = 2n2 + 2n + 1
Un triangle rectangle dont les côtés constituent un triplet pythagoricien est aussi qualifié de pythagorique et le triangle correspondant au cas a = 3, b = 4, c = 5 se rencontre parfois sous le nom de triangle d'or mais le qualificatif est plutôt réservé aux triangles de Penrose : on parle plutôt ici de triangle égyptien : les arpenteurs de l'Antiquité connaissaient bien la propriété d'une corde à nœuds de 12 éléments (3 + 4 + 5) pouvant jouer le rôle d'équerre.
Le rectangle de côtés 3 sur 4 est aussi appelé rectangle pythagoricien : ses côtés et ses diagonales sont des nombres entiers, ce qui n'est pas vraiment courant... :
Précisons, à la gloire des babyloniens, que la tablette Plimpton 322 dresse une liste de nombres écrits en base 60 qui s'avèrent de la forme
a = n2 - p2 , b = 2np , c = n2 + p2
vérifiant donc bien :
a2 + b2 = c2 car (n2 - p2)2 + (2np)2 = n4 - 2n2p2 + p4 + 4n2p2 = (n2 + p2)2 = c2
Étude et recherche des triades
(programmation)
:
Une autre forme pour ces triplets, que l'on pourra étudier à titre d'exercice,
est la suivante : a = 2n + p, b = 2n + q, c = 2n + p
+ q avec pq = 2n2.
Et si p et q sont premiers entre eux, il en est de même de a, b et c.
Pour les petits curieux, si on remplace les carrés par des cubes, on pénètre
dans le célèbre problème de Fermat : ne cherchez
pas, il n'y a pas d'exemple ! Et si, au lieu d'une somme de deux termes, on en
écrit 3, on a un joli cas de quadruplet cubique... :
33 + 43 +53 = 63.
| Table de Pythagore : |
On nomme ainsi un tableau à double entrée indiquant à l'intersection d'une ligne et d'une colonne le résultat d'un opération comme, à gauche, la table de multiplication des chiffres décimaux.
Attribuée à Pythagore (avec les chiffres et nombres de son époque), son procédé de formation est le suivant : on écrit les chiffres de 1 à 9 en 1ère ligne et les doubles en seconde ligne. Puis, pour chaque ligne suivante, la ligne du dessus augmentée de la 1ère : c'est une méthode additive.
On voit se former en 1ère colonne les chiffres de 1 à 9 et le résultat d'une
multiplication comme 67
est lu à l'intersection de la ligne 6 et de la colonne 7 ou vice versa.
On trouve encore souvent ces tables, au dos des cahiers de brouillon des élèves de l'école primaire sous la forme ci-dessous. On les utilise aussi afin de visualiser les composés de deux éléments dans un groupe fini : c'est alors un carré latin.
| Moyenne arithmétique, géométrique et harmonique : |
Les Pythagoriciens améliorèrent les calculs fractionnaire et décimal, hérités des égyptiens, en s'appuyant sur les propriétés des proportions et des diverses notions de moyenne. Pour deux nombres, il s'agit des moyennes :
arithmétique :
(a + b)/2, géométrique
: 
=
(ab)1/2 ,
harmonique : (1/a + 1/b)/2
trapèze & segment médian ,
casse-tête moyen... ,
trapèze & diagonales
Pourquoi cette appellation
géométrique ? si x
est la racine carré de ab, alors x2 = ab ou x/a = y/b : on dit
aussi que x est la moyenne proportionnelle
de a et b. Géométriquement, on se ramène à une quadrature (aire d'un
carré) chère aux grecs de l'Antiquité : x est le côté du carré qui aurait
même aire que le rectangle de mesures a et b.
Pourquoi cette appellation
harmonique ? allusion
à la musique, également chère au musicologue qu'était Pythagore : Il s'agit
de la moyenne arithmétique des inverses, c'est à dire musicalement de la
moyenne arithmétique des fréquences, inverses
de la période.
En savoir plus :
Série harmonique : Division harmonique :
| La découverte des nombres irrationnels, notion de racine carrée et distinguo rationnel, irrationnel : |
Le théorème de Pythagore appliqué au triangle rectangle ABC construit dans un carré ABCD de côté a, conduit à écrire : AC2 = a2 + a2 = 2a2
La diagonale du carré apparaît donc comme le produit
de a par un nombre dont le carré est 2 : il s'agit de la
racine carrée
de 2, notée
2 : 2
x
2 = (2)2
= 2. La diagonale
[AC] mesure a2.
2 =
1,414213562...
La diagonale AE du cube s'obtient en utilisant le
théorème de Pythagore dans le triangle AEF,
rectangle en F : AE2 = FE2
+ AF2 = (a2)2
+ a2 = 3a2.
Par suite AE = a3 : la racine
carrée de 3 est le nombre dont le carré est 3.
3 =
1,732050808...
Rudolff et le signe
:
Un rectangle a exactement pour mesures 3 +
3 (longueur) et 3 -
3 (largeur).
Calculer les valeurs exactes de son périmètre p, de son
aire a
et de ses diagonales d.
Rép. :
p = 12, a = 6, d =
24 = 26
racine carrée : auto-évaluation niveau 3ème
La philosophie de Pythagore, transmise par les Pythagoriciens (disciples de Pythagore qui propagèrent sa pensée dans tout l'empire grec) reposait sur l'explication harmonieuse de toute chose par les nombres entiers. Dans leur science des nombres, les Pythagoriciens incluaient les fractions : quotients non effectués de deux entiers. Cette vision du Monde fut alors sérieusement ébranlée lorsqu'ils ne purent trouver d'entiers m et n tels que m2 = 2n2 afin d'évaluer rationnellement la diagonale du carré.
L'incommensurabilité
de la diagonale d'un carré (et d'un cube) avec son côté, sera
prouvée
par Aristote et donnera naissance aux
nombres dits
irrationnels,
s'opposant à rationnel (étymologiquement que
l'on ne peut pas compter, du latin ratio signifiant compte).
Ainsi commence la longue construction des
nombres réels.
Les
mathématiciens grecs et arabes ont dès lors cherché à mettre en œuvre des
algorithmes de calcul approché d'une racine carrée. Parmi les plus connus, on
peut citer Théon de Smyrne,
Théon d'Alexandrie,
Aryabhata, Al-Khwarizmi
et, tout particulièrement car sa méthode basée sur le
système décimal positionnel (notre système
actuel) et l'identité (a + b)2 = a2
+ 2ab + b2 fut employée jusque dans les années
1950, Ibn al-Banna al Marraqshi (1256-1321) qui vécut à Marrakech (Maroc).
Algorithme d'extraction selon Al-Banna :
Racine carrée, cubique, n-ème dans ChronoMath :
Nombre rationnel :
Rappelons qu'un nombre est
dit
rationnel
s'il peut s'écrire sous la forme a/b (fraction)
où a et b sont des nombres entiers relatifs (b positif non
nul).
2/3, -3/4 sont rationnels. 2/3 n'est pas décimal car il possède une infinité de décimales. 0,666 ou 0,6667 ne sont que des approximations décimales (et rationnelles 0,666 = 666/1000) de 2/3. -3/4 est décimal : on peut l'écrire -0,75.
L'ensemble des nombres rationnels, noté Q (Q comme quotient)
constitue un corps commutatif.
Construction du corps des nombres
rationnels : Peano et les notations ensemblistes :
Dedekind , Meray
, Weierstrass ,
Cantor
Pour qu'un nombre possédant une infinité de décimales soit rationnel, il faut et il suffit que la suite de ses décimales soit périodique car, pour un nombre rationnel a/b, dans la division de a par b, les restes ne peuvent excéder b - 1. On obtient la même suite de décimales au bout d'au plus b divisions (si tous les restes sont différents).
1/7 = 0,14285714285714285714285714285714... : la période est de longueur 6 = 7 - 1
2/9 = 0,222222222... : la période est de longueur 1.
On considère le nombre x =
0,538461538461538461... développement décimal illimité de longueur
6.
Donner l'expression rationnelle (fractionnaire) de x.
Indication :
calculer 1000000x - x. Remarquer ensuite que 59289 est divisible par
9, puis que 37037 est divisible par 37. Noter aussi que 1001 est
divisible par 7, puis... Rép :
x = 7/13
Théodore de Cyrène ,
Al-Biruni ,
Galilée, Cauchy, Weierstrass ,
Méray , Dedekind , Cantor
| Notion d'angles alternes-internes, somme des angles d'un triangle, angles correspondants : |
Selon Proclus, la notion d'angles alternes-internes, mise clairement en place par Euclide dans ses Éléments (Livre I, proposition 27 à 29) fut utilisée auparavant par les Pythagoriciens qui énoncèrent :
la somme des angles d'un triangle égale deux angles droits (angle plat)
Il suffit de tracer la droite (d) passant par A et parallèle à (BC).
Les parallèles (d) et (BC) sont coupées par la sécante (AB) : elles déterminent donc des angles alternes-internes de même mesure : ^A1 = ^B1. De même ^A3 = ^B3, d'où le résultat.
Cette propriété fondamentale fera l'objet de la proposition 32 du livre I des Éléments d'Euclide. Depuis Hipparque, on peut aussi énoncer :
Dans tout triangle la somme des mesures des angles égale 180°
preuve élémentaire (niveau 6ème)
Rappel
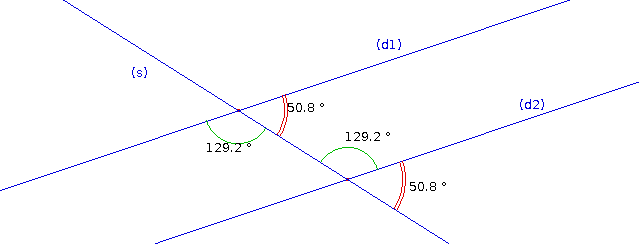
: Deux droites (d1) et (d2) coupées par une sécante (s) déterminent des
angles dits alternes-internes (en vert). Ainsi
appelés car ils ils sont de part et d'autre de la sécantes (ils alternent)
et ils sont à l'intérieur (internes) de la bande formée par les droites
(d1) et (d2). Les angles marqués en rouge sont dits
correspondants. On a le résultat suivant :
Pour que (d1) et (d2) soient parallèles, il faut et il suffit que les angles alternes-internes ou correspondants formés avec une sécante quelconque (s) soient de même mesure.
Vous pouvez faire pivoter
(d1) ou (d2)
Somme des angles au sommet d'une
pyramide :
|
|
| L'étude des polygones et polyèdres réguliers : |
Les Pythagoriciens
connaissaient parfaitement les polygones
réguliers. Ils furent les premiers à
s'intéresser aux polyèdres
réguliers, dits aussi
communément polyèdres de Platon
: ils construisirent le cube (6 faces), le tétraèdre (4
faces) et le dodécaèdre (12 faces); on sait depuis
Descartes
qu'il n'y en a que cinq, avec l'octaèdre (8 faces) et
l'icosaèdre (20 faces).
Le symbole de la secte pythagoricienne était le pentagramme, pentagone étoilé constitué des diagonales du pentagone régulier, également appelé pentacle, lequel possède de nombreuses propriétés géométriques et numériques : le rapport de la diagonale au côté est le célèbre nombre d'or Φ :
Petit exercice sur le pentagramme
(niveau 6ème) , et niveau
1ère (plus dur...)
La forme pentagonale régulière
semble avoir fasciné penseurs, architectes, constructeurs, depuis l'antiquité.
Il est vrai, de surcroît, qu'elle se rattache aux fameux nombre d'or...
On peut évoquer la représentation symbolique des étoiles du ciel, les symboles
religieux, de très nombreux drapeaux, la plupart des distinctions honorifiques,
le constructeur Chrysler, le Pentagone (ministère américain de la
défense), ...
Considérations sur le nombre d'or et la
section dorée :
A
gauche, la médaille de la Légion d'honneur. A droite, le drapeau turc, le croissant,
rappelle la période de début du Ramadan : premier croissant qui suit la nouvelle
Lune, 9ème mois (lunaire) de l'année musulmane.
L'étoile à 5 branches rappelle les 5 prières quotidiennes et les 5 piliers (commandements) de l'Islam : il n'y a de dieu que Dieu et Muhammad est son prophète, la prière, le jeûne pendant le mois de Ramadan, l'aumône, le pèlerinage à la Mecque.
Vidéos sur Pythagore (et bien d'autres) sur
YouTube
(en français) :
Zénon
