
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Appl. affine (déf.) | Affinité | Dilatation | Homothétie | Projection | Symétrie centrale | Symétrie /une droite ou plan | Translation | Transvection Isométries du plan et de l'espace (déplacements et antidéplacements) | Similitudes | Interprétation complexe des similitudes du plan |
 La
plupart des paragraphes de cette
page nécessite généralement la connaissance des
espaces vectoriels et des
applications linéaires et, dans une moindre mesure,
des matrices et des
déterminants.
On trouvera toutefois tout au long de cette page des exercices et des exemples de niveau collège
et lycée (fonctions linéaires et affines, transformations affines élémentaires).
La
plupart des paragraphes de cette
page nécessite généralement la connaissance des
espaces vectoriels et des
applications linéaires et, dans une moindre mesure,
des matrices et des
déterminants.
On trouvera toutefois tout au long de cette page des exercices et des exemples de niveau collège
et lycée (fonctions linéaires et affines, transformations affines élémentaires).
Le terme affine nous vient du latin affinis, adjectif signifiant voisin, lié, associé : penser au mot affinité, du latin affinitas = alliance, ressemblance, sympathie envers une personne. Ce qualificatif se rencontre en biologie pour désigner des espèces proches.
Au sens mathématique, les applications affines, ou transformations affines, sont celles qui conservent certaines propriétés géométriques comme le milieu d'un segment, l'alignement, le barycentre d'un système de points (propriété caractéristique qui nous servira pour leur définition), le parallélisme, le rapport des aires, le rapport des distances et des mesures algébriques, les contacts, le birapport de quatre points alignés.
La conservation des distances et des angles n'est généralement pas assurée. Ce sera cependant le cas des isométries, bijections affines conservant les distances, l'orientation étant conservé dans le cas des déplacements, rotation par exemple. Plus généralement, une transformation conservant les angles est dite conforme : c'est le cas de la similitude (bijection affine) et de la projection Lambert (projection conique, non affine).
i Certains auteurs réservent le terme transformation affine aux applications affines bijectives. Une projection n'est pas bijective mais elle transforme cependant une figure géométrique en une figure géométrique. Mieux vaut parler de bijection affine.
Dès le collège, en classe de 3ème, on rencontre la notion de fonction affine en tant que fonction numérique f : x → mx + b dont la représentation graphique est une droite du plan. à cette fonction on associe la fonction linéaire φ : x → mx, dont la représentation graphique lui est parallèle et passe par l'origine.
Cette fonction numérique φ vérifie φ(x + y) = φ(x) + φ(y) et φ(k.x) = k.φ(x) : c'est la première application linéaire rencontrée dans l'enseignement secondaire. Cette notion se généralise au plan (dimension 2) et à l'espace (dimension 3), voire à des espaces "affines" de dimension n quelconque.
Notion élémentaire de fonction : » Fonctions affines et droites du plan (niveau collège) : »
∗∗∗
Exercices sur fonctions linéaires et affines - Exercices niveau 3ème/2nde
|
Dialogue affine fonctions affine et linéaire, détermination, vérification graphique |
|
Degrés Fahrenheit et degrés Celsius fonction affine |
|
Abonnement fonction linéaire et fonction affine, représentation graphique |
| Gaine électrique fonction affine par intervalles, valeur absolue |
|
Autres nombreux exercices tout au long de cette page |
Dans toute la suite, afin de simplifier les notations vectorielles, une écriture en italique gras, comme OM, indiquera systématiquement un vecteur et pour tout point, comme A, B, M, ..., les notations A', B', M' désigneront les images de ces points par une application (affine) précisée par le contexte. Rappelons ici que l'on peut construire les vecteurs du plan ou de l'espace à partir du concept de bipoints équipollents défini par Bellavitis.
| Notion d'espace affine, repère affine, sous-espace affine : |
♦ Les notions exposées font appel à une conception élémentaire d'un espace affine : espaces de points ε associés (on dit aussi attachés) à un espace vectoriel E sur R (parfois qualifié sous-jacent) lié à ε par les propriétés (axiomes) suivantes :
Pour tout vecteur v de E, pour tout point O de ε, il existe un unique point M tel que OM = v.
Pour tout triplet A, B, C de ε, on a (relation de Chasles) : AB + BC = AC.
➔ Pour une définition générale abstraite basée sur le concept de groupe opérant sur un ensemble, voyez cette page.
♦ Un repère affine d'une droite, d'un plan, de l'espace est la donnée, respectivement, d'un couple (A,B) de points distincts, d'un triplet (A,B,C) de points non alignés, d'un quadruplet (A,B,C,D) de points non coplanaires.
Par exemple, dans le plan,
la donnée de trois points O, I et J non alignés permet de définir le repère (O,I,J)
d'origine O, de
base (OI,OJ). Les points I et J
sont les points unités.
En posant OI = i et OJ = j,
le repère (O,I,J) peut également se noter (O,i,j).
Comme dit en introduction, on s'intéresse ici au plan (dimension 2) et à l'espace (dimension 3) mais on peut aisément généraliser à toute dimension finie : les points de ε sont étudiés (repérés) dans un repère (O,i,j) en dimension 2 et (O,i,j,k) pour la dimension 3.
➔ On notera qu'un singleton {A}, ensemble réduit à un point, peut être considéré comme un espace affine associé à l'espace vectoriel {0} réduit au vecteur nul. Un tel espace ne possède pas de repère. On peut décider que sa dimension est nulle.
Repère orthonormé : »
La notation M(x,y,z) désigne un point d'abscisse x, d'ordonnée y, de cote z. Les nombres x, y et z sont aussi les coordonnées du vecteur OM; on notera encore OM(x,y,z).
♦ Soit Φ un sous-ensemble non vide d'un espace affine ε, A un point de Φ et F un sous-espace vectoriel de E. Φ est qualifié de sous-espace affine de direction F passant par A pour exprimer que pour tout point M de Φ on a AM ∈ F. Si F est de dimension p (p ≤ n), on dit également que p est la dimension de Φ.
Cette définition ne dépend pas du point A choisi dans Φ pour le définir : si B est un point de distinct de A, on a BA = -AB ∈ F, par conséquent BM = BA + AM ∈ F ⇔ AM ∈ F.
Une droite (resp. plan) affine est un sous-espace affine de dimension 1 (resp. 2) dans un espace affine de dimension 3.
Deux points A et B d'un espace affine ε définissent une unique droite notée (AB) passant par A et B, de direction AB (ou de vecteur directeur AB).
Droites du plan et de l'espace : »
Trois points non alignés d'un espace affine ε de dimension 3 définissent un unique plan noté (ABC) passant par A, B et C, de direction le plan vectoriel dont une base est (AB, AC).
| Droite affine, équations d'une droite : |
Dans le plan ou l'espace, une droite (d) est un sous-espace affine de dimension 1. Elle est définie par un des ses points A et un vecteur directeur u (non nul). La droite vectorielle engendrée par u constitue sa direction : tout vecteur non nul colinéaire à u est un vecteur directeur de (d). On parle de droite passant par A dirigée par u.
M est un point de (d) ⇔ il existe un réel α tel que AM = αu
Exemple : dans l'espace, α désignant un nombre réel quelconque, l'ensemble des points M(1,0,α) est la droite passant par A(1,0,0) et dirigée par k. En effet, OM = i + αk; posons OA = i; on a : OM - OA = AM = αk
! si, dans le plan, deux droites sans point commun sont parallèles, il n'en est
pas de même dans l'espace :
deux droites disjointes ne sont pas nécessairement
parallèles !
Dans un plan affine, toute droite possède une équation cartésienne de la forme :
ax + by + c = 0 , (a,b) ≠ (0,0)
pouvant se ramener à la forme y = a'x + b' si b est non nul, mais dans l'espace, une telle forme serait celle d'un plan (voir ci-dessous).
➔ Dans l'espace, la droite ne possède pas d'équation cartésienne mais seulement une équation paramétrique que fournit les coordonnées du vecteur AM = αu : soit, en notant A(xA, yA, zA), M(x, y, z) et u(a,b,c) :
x = xA + αa , y = yA + αb, z = zA + αc , α paramètre décrivant R.
∗∗∗
Cosinus directeurs d'une droite de l'espace
Comme on le verra ci-dessous, on peut cependant caractériser une droite de l'espace par deux équations cartésiennes de plans dont elle sera l'intersection :
| Plan affine, équations d'un plan affine de l'espace 3D, hyperplan : |
Dans l'espace 3D, un plan (P) est un sous-espace affine de dimension 2. Il est défini par un des ses points A et un couple (u,v) de vecteurs linéairement indépendants précisant sa direction : plan vectoriel directeur de (P), engendré par u et v que nous notons (π) :
M est un point de (P) ⇔ il existe deux réels α et β tels que AM = αu + βv
On dira que (A,u,v) est un repère du plan (P). L'espace étant rapporté à un repère (O,i,j,k), en posant M(x,y,z), l'équivalence ci-dessus se ramène à l'équation paramétrique du plan avec A(a, a', a") u(b, b', b"), v(c, c', c") et :
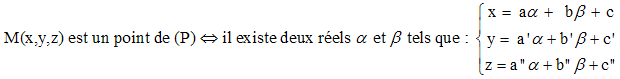

Équation cartésienne du plan :
Les égalités ci-dessus se résument à la forme équivalente ci-dessous, unique à un coefficient multiplicatif près :
mx + ny + pz + q = 0 (eqp)
Preuve : la preuve la plus simple consiste à munir l'espace 3D de la structure d'espace euclidien usuel (niveau 1èreS/TerS) et utiliser la notion élémentaire de produit scalaire en écrivant que si w(m,n,p) désigne un vecteur orthogonal au plan (π), plan vectoriel directeur de (P), M est un point de (P) si et seulement si le vecteur AM de coordonnées (x - a, y - a', z - a") est orthogonal à w, c'est à dire m(x - a) + n(y - a') + p( z - a") = 0, ce qui peut s'écrire mx + ny + pz + q = 0 en posant q = - ma - na' - pa".

➔ Une équation cartésienne de (π) est ainsi mx + ny + pz = 0 et toute droite (d) orthogonale à (P) a pour direction w(m,n,p).
La notion d'hyperplan :
La notion de plan dans l'espace, sous-espace affine de dimension 2 = 3 - 1, se généralise en dimension n > 2 avec la notion d'hyperplan, sous-espace de dimension n - 1. On démontre qu'un hyperplan possède une équation cartésienne généralisant celle du plan donnée ci-dessus en (eqp).
∗∗∗
Vérifier que dans l'espace 3D, l'ensemble (P) des points M(x,y,z) tels que x - 2y + z = 1 est un
plan passant
par A(3,1,0) de direction (u,v) = (i - k, j + 2k).
➔ On parle parfois de système d'équations cartésiennes d'une droite de l'espace en considérant celle-ci comme l'intersection de deux plans. Exemple :
∗∗∗
Déterminer la droite (D) de l'espace, intersection des plans d'équations
respectives x - y + z = 2
et x + y = 3z.
Rép :
en exprimant x et y en fonction de z on trouvera que (D) est la droite passant par A(1,-1,0)
dirigée par u(1,2,1)
| Application affine : |
Soit ε un espace affine associé à un espace vectoriel E. Dans toute la suite idε (resp. idE) désignera l'application identique qui à tout point (resp. vecteur) associe ce même point (resp. vecteur). Autrement dit, idε : M → M et idE : v → v. D'une façon générale on utilisera la notation « ' » (prime) pour désigner l'image d'un point M de ou d'un vecteur v par une application.
Définition :
On qualifie d'affine toute application f de ε dans lui même conservant le barycentre de tout couple de points pondérés. En d'autres termes : soit {(A,α) , (B,β)} un couple de points pondérés pour lequel α + β ≠ 0; il existe alors un unique point G de ε tel que αGA + βGB = 0.
f : ε →
ε est dite affine
⇔def
αG'A'
+ βG'B'
= 0
» On peut
résumer en exprimant que
l'image d'un barycentre est le barycentre des
images.
La propriété
d'associativité du barycentre
permet d'affirmer :
Soit (Ai)i = 1,2,...n un système pondéré de points de ε tel que Σαi est non nulle, il existe alors un unique point G de ε tel que :
α1GA1 + α2GA2+ ... αnGAn = 0
f : ε → ε est affine si et seulement si α1G'A'1 + α2G'A'2+ ... αnG'A'n = 0
Théorème fondamental :
Soit O un point quelconque de ε. Une application f de ε dans lui même est affine, si et seulement s'il existe une application linéaire φ (endomorphisme) de L(E) tel que pour tout M de ε :
M' = f(M) ⇔ O'M' = φ(OM) avec O' image de O par f (r1)
On dit que φ est l'endomorphisme associé à f ou que φ est la partie linéaire de f.On peut écrire (r1) sous la forme :
M' = f(M) ⇔ OM' = φ(OM) + OO' avec O' image de O par f (r2)
La condition
est nécessaire :
Supposons f affine; fixons O dans
ε. Soit V un vecteur
quelconque de E; il existe un unique point M de
ε tel que V
= OM; posons φ(V) = O'M'.
Montrons que φ est linéaire : pour tout α réel, f conserve le barycentre G de {(M,α) , (O,1-α)} : si α.GM + (1-α)GO = 0 alors αG'M' + (1-α)G'O' = 0. C'est dire que si OG = αOM, alors O'G' = αO'M'. Ainsi :
φ(α.V) = φ(αOM) = φ(OG) =def O'G' = αO'M' = αφ(V)
Maintenant, si V et W sont deux vecteurs quelconques de E, il existe un unique couple de points M et P de ε tels que V = OM et W = OP. Puisque f conserve le barycentre, elle conserve l'isobarycentre G de {(M,1) , (P,1)}. C'est dire que si GM + GP = 0 alors G'M' + G'P' = 0 ou encore si 2OG = OM + OP, alors 2O'G' = O'M' + O'P'. Ainsi :
φ(V + W) = φ(OM + OP) = φ(2OG) = 2φ(OG) =def 2O'G' = O'M' + O'P'
soit φ(V + W) =def φ(OM) + φ(OP) = φ(V) + φ(W) : l'application φ est donc bien linéaire.
La condition
est suffisante :
Soit G le barycentre de {(A,a) , (B,b); on a la
relation a.GA + bGB =
0;
par linéarité de φ : aφ(GA)
+ bφ(GB)
=
0,
soit aG'A' + bG'B' =
0;
ce qu'il fallait démontrer.
φ
ne dépend que de f :
Il
est important de vérifier que φ ne dépend pas du point O
choisi. Or, si A et B
sont deux points de ε
avec A' = f(A), B' = f(B), alors, selon la
formule de Chasles, AB =
OB - OA
et on a : A'B' = φ(AB).
♦ Lorsque E = R, noter
le lien entre applications linéaire φ(x) = ax et affine f(x) = ax + b avec u = b.
| Expression analytique d'une application affine et de sa partie linéaire : |
Lorsque l'espace affine ε est de dimension finie n et rapporté à un repère (O,e1, ..., en), on note M(x,y,z,...), M'(x',y',z',...) l'image de M par f et O'(α, β, γ, ...) celle de O dans ce repère. Eu égard à la linéarité de l'endomorphisme φ associé à f, la relation OM' = φ(OM) + OO' peut s'écrire matriciellement OM' = A × OM + OO' ou plus simplement M' = A × M + u :

où A est la matrice de φ dans la base (e1, ..., en) et une telle écriture caractérise une application affine. Comme dans le cas linéaire, on appelle expression analytique de f, la donnée des coordonnées x', y', z', ... de f(M) en fonction de celles de M.
Des coordonnées x', y', z', ... de M' = f(M) polynomiales de degré 1 en x, y, z, ... caractérisent une application affine f : ε → ε.
Partie linaire d'une application affine :
Les nombres x', y', z', ... sont des combinaisons linéaires de x, y, z, ... éventuellement augmentées d'un scalaire et ces formes caractérisent les applications affines. Lorsque tous les scalaires sont nuls (u = 0), c'est que l'origine O du repère (O,e1, ..., en) de ε est invariante et une telle application affine s'identifie à son endomorphisme associé φ :

Tout comme son endomorphisme, et dans ce contexte, cette partie de l'expression analytique de f est qualifiée de partie linéaire.
|
Propriétés générales des applications affines, groupe affine : |
♦ Convention d'écriture pratique :
Une origine quelconque O étant choisie dans ε, se donner un point M revient à se donner le vecteur OM. La relation (r2) OM' = φ(OM) + OO' peut alors s'écrire M' = φ(M) + O' ou bien M' - O' = φ(M) exprimant O'M' = φ(OM).
Une écriture comme M + u caractérisera l'image M' du point M par la translation de vecteur u : OM' = OM + u.
Écrire M' = f(M + u) revient à exprimer le vecteur φ(OM + u) = φ(OM) + φ(u); donc f(M + u) = f(M) + φ(u).
Soit f une application affine de l'espace affine de ε, d'espace vectoriel sous-jacent E, d'endomorphisme associé φ.
♦ p0/ la relation (r2), OM' = φ(OM) + u , avec u = OO' montre que l'application affine f est entièrement déterminée par son endomorphisme et l'image d'un point quelconque du plan.
♦ p1/ Si A est un point de ε, l'application constante f : M → A est une application affine dont l'endomorphisme associé est l'application linéaire nulle θ : v → 0. En effet, on a pour tout M, OM' = θ(OM) + u avec u = OO' = OA.
♦ p2/ L'application affine f est entièrement déterminée par l'image d'un repère affine de ε.
♦ p3/ Si f et g sont affines d'endomorphismes associés respectifs φ et ψ, il en est de même de la composée g o f dont l'endomorphisme associé est alors ψ o φ. Ce résultat permet de décomposer une application affine en un produit de composition.
♦ p4/ Si f et g sont affines toute combinaison linéaire de f et g est affine. En ce sens que dans un repère de ε, M → M' = (f + g)(M) signifie que les coordonnées de M' sont celles de f(M) augmentées de celles de g(M) et M → M' = αf(M) signifie que les coordonnées de M' sont celles de f(M) multipliées par α. Avec les notations précédentes, l'endomorphisme associé à αf + βg est αφ + βψ.
Soit f définie par M(x,y) →
M'(x + y, 2y-1) et g par M(x,y) → M'( y, 1 - x); alors :
f + g : M(x,y) → M'(x + 2y, 2y-x) , 2f - 3g : M(x,y) → M'(2x -
y, 3x + 4y - 5)
Si s est une symétrie (s o s = idε), alors p : M → M' = ½(M + s(M)) est une projection (p o p = p).
Si p est une projection (p o p = p), alors αidε + (1 - α)p : M → M' = αM + (1 - α)p(M) est une affinité.
Exemples usuels de décomposition : »
♦ p5.1/ Pour qu'une application affine f soit bijective il faut et il suffit que sa partie linéaire φ le soit. Pour qu'il en soit ainsi, il faut et il suffit que le noyau de φ soit réduit à {0}
Preuve : soit φ l'endomorphisme associé à f. L'expression analytique de f s'écrit symboliquement M' = A×M + u où A est la matrice de sa partie linéaire. On peut ainsi décomposer f sous la forme f = tu o φ : M → A×M → A×M + u, tu désignant la translation de vecteur u. La translation étant une bijection, si φ est bijective, f l'est aussi en tant que composée de deux bijections. Inversement si f est bijective, en composant par la translation réciproque de vecteur -u, on peut écrire t-u o f = φ et conclure.
♦ p5.2/ Si f est une application affine bijective d'endomorphisme associé φ, sa réciproque f-1 est également affine.
Preuve : On a f = tu
o φ et M' = f(M) ⇔ M =
f![]() -1(M'). f
-1(M'). f![]() -1
= (tu o φ)-1
= φ-1 o t-u , d'où :
f
-1
= (tu o φ)-1
= φ-1 o t-u , d'où :
f![]() -1(M')
= A-1
-1(M')
= A-1![]() ×
×![]() (M' - u) =
A-1
(M' - u) =
A-1![]() ×
×![]() M' - A-1
M' - A-1![]() u. L'application réciproque de f est donc affine,
d'endomorphisme associé φ-1 (de
matrice A-1), l'image de
l'origine est fournie par A-1
u. L'application réciproque de f est donc affine,
d'endomorphisme associé φ-1 (de
matrice A-1), l'image de
l'origine est fournie par A-1![]() u.
u.
Considérons l'application affine
f définie par x' = 2x + y + 1 , y' = 7x + 4y - 1.
φ
a pour matrice
A =
 , son déterminant est 1 ≠ 0;
φ
est donc bijective et il en est donc de même de f (selon p5).
La matrice inverse de
φ, à savoir celle de φ-1,
est A-1 =
, son déterminant est 1 ≠ 0;
φ
est donc bijective et il en est donc de même de f (selon p5).
La matrice inverse de
φ, à savoir celle de φ-1,
est A-1 =
 ; on l'applique
à u(1,-1), ce qui nous conduit à l'expression analytique de f
; on l'applique
à u(1,-1), ce qui nous conduit à l'expression analytique de f![]() -1
: M' → M
:
-1
: M' → M
:  , soit : x =
4x' - y' - 5 , y = -7x' + 2y' + 9. Vérifions ce résultat en recherchant à
exprimer x et y en fonction de x' et y' à partir de l'expression analytique
de f : on est conduit au système 2x + y = x' - 1 , 7x + 4y = y' + 1. On
trouvera aisément x = 4x' - y' - 5 , y = -7x + 2y' + 9.
, soit : x =
4x' - y' - 5 , y = -7x' + 2y' + 9. Vérifions ce résultat en recherchant à
exprimer x et y en fonction de x' et y' à partir de l'expression analytique
de f : on est conduit au système 2x + y = x' - 1 , 7x + 4y = y' + 1. On
trouvera aisément x = 4x' - y' - 5 , y = -7x + 2y' + 9.
Groupe affine :
L'ensemble des applications affines bijectives de
ε est un
groupe (non commutatif) pour la loi de composition des applications
noté
GA(ε) et l'application f → φ est un
morphisme de GA(ε)
dans le groupe linéaire GL(E).
♦ p6/ Si l'application affine f admet deux points invariants A et B, alors tous les points de la droite (AB) sont invariants par f.
Preuve : soit K un point quelconque de (AB) autre que A et B. K s'écrit comme barycentre de A et B : il existe deux réels a et b tels que aKA + bKB = 0. On a alors, avec K' = f(K) : φ(aKA + bKB) = φ(0), c'est à dire aK'A + bK'B = 0 et l'unicité du barycentre prouve que K' = K.
♦ p7/ la conservation du barycentre permet d'affirmer qu'une application affine bijective transforme :
♦ p8/ Si U est un sous-espace vectoriel de E ({0}, droite vectorielle, plan vectoriel, E lui-même), l'image par f du sous-espace affine (singleton, droite affine, plan affine, ε lui-même ) passant par A et dirigé par U est le sous-espace affine passant par A' = f(A), dirigé par φ(U) et de même dimension que ce dernier.
♦ p9/ l'ensemble U des points invariants par l'application affine f, à savoir les points M tels que f(M) = M, est soit vide, soit un point, soit un sous-espace affine propre (droite, plan) passant par un tel point et dirigé par le sous-espace vectoriel V des vecteurs invariants par φ.
Preuve : M = f(M) ⇔ OM = φ(OM) : rechercher l'ensemble U des points invariants par f revient donc à rechercher le sous-espace vectoriel V des vecteurs invariants par son endomorphisme associé φ. Le cas U vide ou réduit à un point (singleton) correspond à V = {0}.
♦ p10/ Une application affine conserve les rapports des mesures algébriques de trois points alignés et, par conséquent, le birapport de quatre points alignés.
Preuve : soit trois points alignés A, B et C et considérons par exemple AB et AC : il existe un réel k tel que AB = kAC. Avec les notations précédentes, φ(AB) = A'B' = kφ(AC) = kA'C' : c'est dire que si AB/AC = k, il en est de même de A'B'/A'C'. Si on considère maintenant un birapport [A,B,I,J] = IA/IB : JA/JB, les deux rapports IA/IB et JA/JB sont conservés, donc également leur rapport.
|
Un contre-exemple d'application affine : la projection centrale |
Dans le plan ou l'espace, la projection centrale n'est pas une application affine; ci-dessous est illustrée la projection de centre (ou sommet) O sur un plan (P).

! Une droite (AB) se projette sur (P) en (A'B'). Une telle transformation ne conserve pas les milieux (isobarycentre) car si J est le milieu de [AB], J' n'est généralement pas le milieu de [A'B'] : ce n'est donc pas une application affine.
Notion de géométrie projective
:
»
|
La translation : |
a/ Soit u un vecteur du plan (ou de l'espace) et t l'application qui à tout point M associe M' tel que MM' = u. On dit que t est la translation de vecteur u. M' est l'image de M (on dit souvent aussi translaté de M) dans la translation de vecteur u :

b/ Si t(A) = B et t(C) = D alors AB = CD = u et le quadrilatère ABDC (dans cet ordre !) est un parallélogramme. Inversement, si ABCD (dans cet ordre !) est un parallélogramme, alors AB = DC et AD = BC. On peut dire, par exemple, que B est l'image de A dans la translation de vecteur DC.

c/ Considérons une translation t de vecteur u lorsque le plan (ou l'espace) est rapporté à un repère d'origine O (figure ci-dessous). Selon la formule de Chasles, si M' = t(M) alors MM' = u peut s'écrire OM' - OM = u ou encore OM' = OM + u . Si u est non nul, t(M) = M ne peut avoir lieu :

♦ Une translation est une application affine dont l'endomorphisme associé est l'application identique
idE : v → v; la translation de vecteur non nul n'admet aucun point invariant. C'est une bijection dont la réciproque est la translation de vecteur -u.♦ Inversement, une application affine de partie linéaire idE est une translation.
Remarque : Sans utiliser une origine O, pour tout M et N du plan (ou de l'espace), on a M'N' = M'M + MN + NN' = -u + MN + u = MN = idE(MN), donc t est l'application affine d'endomorphisme associé idE.

Translation & addition vectorielle, composée de deux
translations (exposé élémentaire) :
»
La translation en tant qu'isométrie :
»
Proposition :
Muni de la loi de composition des applications, l'ensemble T(ε) des translations dans ε constitue
un sous-groupe distingué du groupe affine GA(ε).
Preuve : T(ε)
est un sous-groupe de GA(ε)
: l'application composée de deux translations tu et tv
est la translation tu + v = tv + u :
T(ε) est stable pour la loi o.
Le symétrique d'une translation tu est la translation t-u.
Soit maintenant f une application affine de GA(ε)
de partie linéaire φ. Le sous-groupe des translations est
distingué dans GA(ε)
si, pour tout tu de T(ε), t
= f o tu o f-1 est une translation. La partie linéaire de
t est φ o idE o φ-1 = φ o φ-1
= idE : t est une
translation.
Pour tout M de
ε
: t(M) = (f o tu o f-1)(M)
= f(f-1(M) + u) = M + φ(u) :
t = f o tu o f-1
est la translation de vecteur φ(u).
![]() »
»
![]() voir
convention d'écriture.
voir
convention d'écriture.
Autre preuve : »
| L'homothétie : |
Soit A un point du plan (ou de l'espace) et h l'application qui à tout point M associe M' tel que AM' = kAM, k réel non nul (ci-contre, k = 2). On parlera d'homothétie de centre A, de rapport k. Si O est un point du plan (ou de l'espace), on peut écrire OM' = kOM + u avec u = - OA. Ce qui conduit immédiatement à l'expression analytique d'une homothétie (» ci-après)

à l'exception du cas trivial k = 1, on notera que le point A est l'unique point invariant par h.
Si N' = h(N), on aura M'N' = AN' - AM ' = kAN - kAM = kMN, pour tous M et N du plan :
♦ Une homothétie de rapport k est une application affine dont l'endomorphisme associé est l'application linéaire φ : v→ kv, homothétie vectorielle de rapport k. Pour k distinct de 1, elle admet son centre comme unique point invariant.
La matrice d'une homothétie vectorielle
est celle de k.idE![]() .
Soit, lorsque n = 2 et n = 3 :
.
Soit, lorsque n = 2 et n = 3 :
![]() Comme toute application affine, l'homothétie
conserve les contacts
: si deux courbes (c) et (c') sont tangentes en un point I, les images de (c) et (c') par toute homothétie seront tangentes en
l'image de I. »
Chasles
Comme toute application affine, l'homothétie
conserve les contacts
: si deux courbes (c) et (c') sont tangentes en un point I, les images de (c) et (c') par toute homothétie seront tangentes en
l'image de I. »
Chasles
♦ p11/ Les applications affines autres que l'identité, transformant une droite en une droite parallèle sont les translations ou les homothéties
(preuve : ☼).Dilatation et groupe des homothéties-translations : »
∗∗∗
2.
Construction d'un cercle tangent à
deux demi-droites et passant par un point donné
3.
Homothétie centre de gravité et
orthocentre (droite d'Euler)
4.
A, B et C étant trois points du plan, on considère l'application f qui à
tout point M associe M' tel que MM' = MA - 2MB + 4MC
Prouver que f admet un unique point invariant I. Exprimer IM' en fonction de IM; en déduire la nature précise de f.
|
La symétrie centrale ou symétrie par rapport à un point : |
Dans le plan affine ou euclidien de dimension 2, on considère un point A. Soit f l'application qui à tout point M du plan associe le point M' défini par A est le milieu de [MM']. On parle de symétrie par rapport A ou de symétrie (centrale) de centre A, lequel est l'unique point invariant dans cette symétrie.

f : M→M' est une symétrie centrale ssi il existe un point A tel que pour tous M et N, AM + AM' = 0 .
La symétrie de centre A est une application affine car on peut écrire pour tout M, en choisissant A comme origine : AM' = - AM. Son endomorphisme associé est donc - idE : v → -v.
Quels que soient M et N, on a M'N' = -id(MN) = NM : la symétrie centrale conserve les distances, c'est donc une isométrie. Par exemple, elle transforme un cercle (c) de centre K en un cercle (c') de même rayon dont le centre est le symétrique de K. On remarque que f o f = id : M→M. Pour cette raison, on dit que f est une involution, cela revient à exprimer que f est une bijection coïncidant avec sa réciproque.
En savoir plus sur la symétrie centrale : »
|
La symétrie par rapport à une droite : » cas vectoriel |
Dans un plan affine ε de dimension 2, on considère une droite (d) et une direction de droite (δ) définie par un vecteur u. Soit f l'application qui à tout point M du plan associe le point M' défini par (MM') // (δ) et H milieu de [MM'], H désignant l'intersection de (MM') avec (d). On parle de symétrie par rapport à (d) parallèlement à (δ) ou suivant la direction u. La droite
(d) est l'ensemble des points invariants dans cette symétrie et le symétrique de M' est M : f o f = id. La symétrie par rapport à une droite est donc involutive, autrement dit une bijection coïncidant avec sa réciproque.Un exemple illustré :
Considérons dans le plan, rapporté à un repère (O,i,j), l'application f qui à tout point M(x,y) associe M'(2x - y + 1, 3x - 2y + 3). On peut écrire OM' = φ(OM) + u où φ est l'endomorphisme défini par v(x,y) → v'(2x - y, 3x - 2y) et u(1;3). f est donc une application affine.
MM' = (x - y + 1).u garde donc une direction fixe, ce qui montre que la droite (d) d'équation x - y + 1 = 0 est l'ensemble des points invariants par f.
Pour tout point M, le milieu de [MM'] de coordonnées α = (3x - y +1)/2 , β = (3x - y + 3)/2 appartient à (d).
f est involutive : on peut le vérifier par le calcul de f o f :
M(x,y) →M'(2x - y + 1, 3x - 2y +3) →M"(2(2x - y + 1) - (3x - 2y +3) +1, 3(2x - y + 1) - 2(3x - 2y + 3) + 3) = M(x,y)


Si votre navigateur accepte les applets
Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déplacer M, la direction u et la droite (d)
♦ p12a/ Si f est une application affine involutive , il en est de même de son endomorphisme associé φ.
Preuve : il suffit, pour s'en convaincre, d'appliquer φ à la relation fondamentale OM' = φ(OM) + OO'
♦ p12b/
Pour toute application affine involutive f et tout point A d'image A', le milieu I de [AA'] est invariant par fPreuve : A" = f(A') = f(f(A)) = (f o f)(A) = A. I le milieu de [AA'] ⇔ IA + IA' = 0. Appliquons φ : I'A' + I'A" = 0 , c'est à dire I'A' + I'A = 0. I est donc le milieu de [AA']. C'est dire que I' = I.
♦ p12c/ Toute involution affine plane f autre que l'identité est une symétrie centrale ou une symétrie par rapport à une droite.
Preuve : Soit J l'ensemble J des points invariants par f. J n'est pas vide car selon p12b, l'ensemble des milieux de [MM'] lorsque M décrit ε en fait partie. J est donc un sous-espace affine (p8) : singleton, droite ou plan lui-même. J n'est pas le plan puisque f n'est pas l'identité. Si J est réduit à un point I, alors I est le milieu de [MM'] pour tout point M du plan : f est la symétrie centrale de centre I. Si J est une droite (d), sa direction est celle de la droite vectorielle des vecteurs invariants par son endomorphisme associé φ (» p6); soit w un représentant de cette direction; on peut définir (d) en tant que droite passant par le milieu de [OO'] (ou par tout autre segment [AA'], A' = f(A) et dirigée par w. L'endomorphisme φ étant involutif, le vecteur MM' vérifie φ(MM') = M'M = - MM' : le vecteur MM' garde une direction fixe, il appartient à la droite vectorielle δ des vecteurs changés par φ en leur opposé. » symétrie vectorielle. f est la symétrie par rapport à (d) de direction δ.
♦ La symétrie par rapport à une droite (d) suivant une direction donnée δ, est une bijection affine involutive M → M' admettant (d) comme ensemble de points invariants, le vecteur MM' gardant la direction δ. Son endomorphisme associé φ est une symétrie vectorielle.
 ! Une application
affine dont l'endomorphisme associé est une symétrie vectorielle (endomorphisme
involutif) n'est pas toujours une symétrie affine :
! Une application
affine dont l'endomorphisme associé est une symétrie vectorielle (endomorphisme
involutif) n'est pas toujours une symétrie affine :
♦ p13/ Une application affine f : M→M', définie par OM' = φ(OM) + u est une symétrie ssi φ o φ= id et φ(u) = -u
La condition est nécessaire car selon la relation fondamentale, on a u = OO', vecteur qui doit donc appartenir à la direction de la symétrie, tant vectorielle que affine. Elle est suffisante, si OM' = φ(OM) + u et φ(u) = - u
, alors, en appliquant φ : φ(OM') = O'M" = (φ o φ)(OM) + φ(u), c'est à dire + OM" = OM - OO', donc M" = M et on applique p12.f définie par x' = 3x - 2y + 1, y' = 4x - 3y est-elle une symétrie affine ? Réponse : non. L'endomorphisme associé φ a pour matrice :
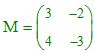
M2 = I (matrice unité), donc φ est involutive : c'est une symétrie vectorielle. Mais on a ici OM' = φ(OM) + u avec u(1,0), donc -u(-1,0). Or :
La direction de la symétrie vectorielle est obtenue en recherchant v(x,y) tel que φ(v) = -v, système fournissant y = 2x.
|
La symétrie orthogonale par rapport à une droite ou symétrie "axiale" et symétrie glissée : » cas vectoriel |
Dans le plan euclidien, on appelle symétrie axiale la symétrie orthogonale par rapport à une droite : le vecteur MM' est perpendiculaire à (d). Cette symétrie conserve les distances : il s'agit d'une isométrie. Les angles géométriques sont conservés mais elle change les angles orientés en leur opposé.
En savoir plus sur la symétrie axiale : »
![]() Dans l'espace euclidien à 3 dimensions, la symétrie orthogonale
par rapport à une droite est une
rotation d'angle π.
Les angles
géométriques sont conservés ainsi que les angles orientés.
Dans l'espace euclidien à 3 dimensions, la symétrie orthogonale
par rapport à une droite est une
rotation d'angle π.
Les angles
géométriques sont conservés ainsi que les angles orientés.
Dans le plan (resp. l'espace), on parle symétrie glissée pour exprimer la composée commutative s o t = t o s d'une symétrie axiale (resp. d'une symétrie par rapport à un plan) de direction (δ) et d'une translation t de vecteur appartenant à (δ). Il s'agit là encore d'une isométrie.
En savoir plus sur la symétrie glissée : »
|
La projection affine : » cas vectoriel (projecteur) |
♦ I - Généralités :
Dans le plan ou l'espace affine ε
(dimension 2 ou 3), on appelle projection une application affine f vérifiant f o f = f. Il s'agit donc d'une application affine idempotente.♦ p14/ L'endomorphisme associé à une projection affine est un projecteur.
Preuve : notons π l'endomorphisme associé à la projection f et soit u un vecteur de E, espace vectoriel sous-jacent à ε, dont un représentant est AB. Notons A' (resp. B'), l'mage de A (resp. B) par f et A" (resp. B") l'image de A' (resp. B') par f. On a A" = A' et B" = B' car f est une projection, et π(u) = π(AB) = A'B'. Or(π o π)(u) = π[π(u)] = π(A'B') = A"B" = A'B' = π(u) : c'est dire que π o π = π; π est un projecteur.
♦ p15/ Toute application affine idempotente (projection) f admet au moins un point invariant et son image coïncide avec l'ensemble de ses points invariants (sous-espace affine de ε). » p8-p9
Preuve : Soit J l'ensemble des points invariants par f et F l'image de ε par f. Puisque f o f = f, on a f(f(M)) = f(M) pour tout point M : J contient F et n'est donc pas vide. Inversement, si M est invariant, alors f(M) = M, donc F contient J. Finalement J = F.
Dans toute la suite, on élimine deux cas triviaux de projection :
a) f = idε : M → M, application identique de ε b) f = cte, application constante qui à tout M de ε associe un même point A.
! Réciproquement, une application affine dont l'endomorphisme associé est un projecteur peut ne pas être une projection. Considérer ce contre-exemple :
Dans un plan affine (P) soit f l'application affine définie par x' = 3x - 6y + 1 , y' = x - 2y - 1. Vérifier que son endomorphisme π est un projecteur mais que f n'admet aucun point invariant : ce n'est pas une projection du plan.
Dans le cas général, selon le théorème fondamental, si A est un point quelconque d'image A' par f, tout point M d'image M' = f(M) vérifie A'M' = π(AM). Notons A" et M", les images respectives de A' et M' par f. On a A"M" = π(A'M') = π(π(AM)) = π(AM). Donc M"= M ⇔ A" = A'.
♦ p16-1/ Une application affine f dont l'endomorphisme associé est un projecteur est une projection sous la condition d'admettre (au moins) un point invariant, auquel cas l'ensemble de ses points invariants n'est autre que son image (selon p15).
♦ p16-2/ Une application affine f : M→M', définie par OM' = φ(OM) + u est une projection ssi φ o φ= φ et φ(u) = 0.
Preuve : la condition est nécessaire car en notant M" = f(M'), la relation fondamentale s'exprime par OM' = φ(OM) + u et conduit, en appliquant φ, à : O'M" = O'M' + φ(u), c'est à dire M'M" = φ(u). Par suite f o f = f ssi φ(u) = 0 : u doit appartenir au noyau de φ, c'est à dire à la direction de cette projection vectorielle. Elle est suffisante, car si OM' = φ(OM) + u et φ(u) = 0, alors, en appliquant φ : φ(OM') = (φ o φ)(OM) = φ(OM) , c'est à dire O'M" = O'M' , donc M" = M'. Par conséquent f o f = f.
♦ p17 (corollaire)/ Pour toute projection affine f d'endomorphisme associé π, le vecteur MM', où M' désigne l'image de M par f, garde une direction fixe, à savoir le noyau de π, sous-espace vectoriel des vecteurs de E dont l'image par π est nulle.
♦ II -
Concrètement (projection plane
sur une droite) :
Dans un plan affine on considère une droite (D) dont un vecteur directeur est u et une
droite ou une direction de droite (δ) définie par un
vecteur v non colinéaire à u. Soit p l'application qui à tout
point M de l'espace associe le point M' = p(M) défini par MM'![]() ∈(δ) et M'∈(D).
Autrement dit, M' est le point d'intersection de (D) avec la
droite (affine) de direction (δ) passant par M. On parle de
projection sur (D) de direction (δ)
ou parallèlement
à (δ).
∈(δ) et M'∈(D).
Autrement dit, M' est le point d'intersection de (D) avec la
droite (affine) de direction (δ) passant par M. On parle de
projection sur (D) de direction (δ)
ou parallèlement
à (δ).

➔
Si u et v sont orthogonaux, c'est à
dire (MM')![]() ⊥
⊥![]() (D) pour tout point M du plan, la projection est dite
orthogonale.
(D) pour tout point M du plan, la projection est dite
orthogonale.
♦
p18/
La projection
p sur une droite (D) suivant la direction - ou parallèlement à - (δ), est une application affine
M
→
M'∈(D)
admettant (D), base de la projection, comme
ensemble de points invariants, (MM') gardant
la direction (δ) pour tout M du plan.
Si u est un vecteur directeur
de (D), l'endomorphisme
associé à p est le
projecteur
de direction (δ) sur la droite vectorielle
engendrée par
u.
∗∗∗
Dans le plan affine 2D,
on considère l'application
f définie par M(x,y) → M'(x',y') = (3x
- y + 1, 6x - 2y +3).
a) Justifier brièvement que f est une application affine.
b) Vérifier sans utiliser l'endomorphisme associé que
f o f = f. c) Préciser les caractéristiques géométriques de cette application.
☼
♦ III - Concrètement (projection de l'espace 3D sur un plan parallèlement à une droite) :
Dans l'espace de dimension 3, on considère un plan (P) et une droite ou une direction de droite (δ). Soit p l'application qui à tout point M de l'espace associe le point M' défini par (MM') // (δ) et M'∈(P) : on peut exprimer M' comme le point d'intersection de (P) avec la droite (affine) de direction (δ) passant par M. On parle de projection sur (P) de direction (δ) ou parallèlement à (δ).

➔
En dimension 3, une projection parallèlement à une droite est parfois qualifiée de cylindrique.
∗∗∗
Dans l'espace affine euclidien
ε
de
dimension 3 rapporté au repère orthonormé (O,i,j,k),
on considère l'application affine f : M → M' définie par
3x' = 2x - y + z + 1 , 3y' = -x + 2y + z + 1 , 3z' = x + y + 2z - 1.
a)
Montrer que f est la projection sur un plan (P) parallèlement à une
droite (δ) en précisant ces deux sous-espaces.
b) Quelle est la particularité de cette projection ?
☼
♦ IV - Concrètement (projection de l'espace 3D sur une droite parallèlement à un plan) :
Dans l'espace de dimension 3, on considère un plan (P) et une droite (D). Soit p l'application qui à tout point M de l'espace associe le point M' défini par (MM') // (P) et M'∈(D) : on peut exprimer M' comme le point d'intersection de (D) avec la droite parallèle à (P) passant par M. On parle de projection sur (P) de direction (δ) ou parallèlement à (δ).

∗∗∗
Dans l'espace affine 3D rapporté à un repère (O, i, j,
k), on considère la droite (D) passant le point A(1,0,1), dirigée par
u(1,2,1)
et le plan (P) d'équation x - 2y + z - 1 = 0. Donner l'expression analytique de
la projection affine sur (D) parallèlement à (P)
☼
|
L'affinité : |
Cette transformation prit naissance avec Euler dans son Introductio in Analysin infinitorum de 1748, écrit en latin. Considérant les courbes semblables, c'est à dire images l'une de l'autre par une similitude (composée d'une homothétie et d'une isométrie) pour lesquelles les rapports des abscisses et des ordonnées est le même, Euler s'intéresse au cas où ces rapports pourraient être distincts. La courbe image présentant alors une certaine affinité avec la courbe initiale (du larin affinitas = alliance, ressemblance). L'avènement de Bourbaki a semé une certaine confusion de vocabulaire en substituant l'appellation dilatation à celle d'affinité. ChronoMath fait le choix de conserver le vocabulaire historique en conservant à la dilatation son ancienne acception étudiée au paragraphe suivant.
Lorsque ε est de dimension n (n ≥ 2), considérons une droite (δ), un hyperplan Φ de ε (sous-espace affine de dimension n - 1, plan dans le cas n = 3) ne contenant pas (δ) et un réel non nul k :
L'affinité de base Φ
parallèlement à (δ), de rapport k, est
l'application qui à tout point M de
ε associe le point M'
défini par
(MM') // (δ) et HM' = k![]() .HM
avec H = p(M), projection de M sur (Φ)
parallèlement à (δ).
.HM
avec H = p(M), projection de M sur (Φ)
parallèlement à (δ).
Appelons f l'affinité définie ci-dessus :
Si k = 1, f est l'application identique de ε : M → M.
Si k = -1, f est la symétrie par rapport à Φ, parallèlement à (δ).

Illustration dans le cas de l'espace 3D (n = 3)
Montrons que f est une application affine :
plaçons-nous dans un repère de
ε
d'origine O situé sur (d). On a alors O' = p(O) = O. L'égalité
HM' = k![]() .HM
peut s'écrire OM' - OH = k.(OM
-
OH) ou encore : OM' = k
.HM
peut s'écrire OM' - OH = k.(OM
-
OH) ou encore : OM' = k![]() .OM
+ (1 - k).OH. Si π
désigne le
projecteur
associé à p, on a π(OM) =
p(O)p(M) = OH. En notant hk l'homothétie vectorielle
de rapport k, on a
:
.OM
+ (1 - k).OH. Si π
désigne le
projecteur
associé à p, on a π(OM) =
p(O)p(M) = OH. En notant hk l'homothétie vectorielle
de rapport k, on a
:
OM' = hk(OM) + (1 - k).π(OM) = [hk + (1 - k)π](OM)
♦ p19a/ Avec les notations ci-dessus, l'affinité est une bijection affine d'endomorphisme associé hk + (1 - k)π = k.idE + (1 - k)π (affinité vectorielle) et dont les points invariants sont ceux de sa base.
Preuve : Selon la proposition p5, il nous faut montrer que φ = k.idE + (1 - k)π est un automorphisme de E (k ≠ 0). Le cas k = 1 étant trivial, on suppose k ≠ 1. L'espace E étant de dimension finie, il suffit de montrer que le noyau de φ est réduit à {0}. Notons Δ l'hyperplan vectoriel dirigeant Φ et supposons k.v + (1 - k).π(v) = 0. Si v ∈ Δ, on a π(v) = v, on en déduit v - k.v = - k.v, donc v = 0. Sinon v peut s'écrire u ⊕ w, u dirigeant (δ) et w ∈ Δ car Φ ne contenant pas (δ), E est somme directe de Δ et de la droite vectorielle dirigeant (δ). On a alors π(v) = w, d'où (1 - k).w = -k.v et k n'étant ni 0, ni 1, v serait un vecteur de Δ, ce qui est contraire à l'hypothèse : v ne peut être que nul.
♦ p19b/ L'affinité réciproque possède les mêmes bases et direction et sa partie linéaire est h1/k + (1 - 1/k)π.
Preuve : ce résultat est géométriquement intuitif. Vu que h1/k o hk = idE et π o π = π, on peut vérifier que [h1/k + (1 - 1/k)π] o [hk + (1 - k)π] = idE.
♦ p20/ Choisissons une base de E comme réunion d'une base de Δ (l'hyperplan vectoriel dirigeant Φ) et d'un vecteur directeur u de (δ). En plaçant en dernière position le vecteur u, La matrice d'une affinité vectorielle est de la forme :
➔ L'affinité plane (n = 2) :
Dans ce cas l'hyperplan Φ est une droite : on considère une droite (d), une direction de
droite (δ) distincte de celle de (d) et un réel non nul k.
L'affinité de base (d), de
direction (δ),
de rapport k
est l'application qui à tout
point M du plan associe le point M' défini par (MM') // (δ)
et HM' = k![]() .HM
où H = p(M), projection de M sur (d)
parallèlement à (δ).
.HM
où H = p(M), projection de M sur (d)
parallèlement à (δ).
i Plutôt que de direction (δ), on dit parfois, voire souvent, parallèlement à (δ) bien que ce soit limite illicite puisqu'il s'agit ici d'une direction de droite caractérisée par un vecteur et non pas par une droite.

affinité de base (d), de direction (δ), de rapport 2
![]() Lorsque la direction (δ) est orthogonale à celle de (d), on
parle d'affinité orthogonale :
Lorsque la direction (δ) est orthogonale à celle de (d), on
parle d'affinité orthogonale :

L'ellipse, image de son cercle principal par affinité orthogonale : »
∗∗∗
1.
Dans le plan euclidien usuel
ε de
dimension 2 rapporté au repère orthonormé (O,i,j), on considère la droite (D)
d'équation 2x - 3y + 1 = 0 et une direction (δ)
définie par le vecteur u(1,1). Donner l'expression analytique de
l'affinité f d'axe (D) de rapport 2, parallèlement à (δ).
2.
Dans le plan euclidien usuel
ε de dimension 2 rapporté au repère
orthonormé (O,i,j), on considère l'application affine f laissant O invariant
et dont l'endomorphisme associé φ vérifie :
φ(i) = 3i , φ(j) = 2j. Montrer que f est la composée de deux affinités.
Théorème :
On démontre que dans le cas d'un espace de dimension finie :
Toute
bijection affine peut se décomposer en un produit d'au plus
trois affinités
(au sens de la composition des applications)
|
La dilatation : |
On appelle dilatation une application affine transformant une droite en une droite parallèle. La caractérisation d'une telle application est étudiée sur cette page : il s'agit d'une homothétie ou d'une translation. Ce résultat conduit à cette définition :
On appelle
dilatation tout composé t o
h d'une homothétie h par une translation t : si A est un point de
ε, k un réel non nul et u un vecteur
de E, à tout point M on associe M' tel que AM' = k![]() AM + u. On parle de dilatation
de centre A, de rapport k, de vecteur u.
AM + u. On parle de dilatation
de centre A, de rapport k, de vecteur u.
Si u = 0, k ≠ 0, la dilatation est l'homothétie de centre A, de rapport k;
Si k = 1, u ≠ 0, la dilatation est la translation de vecteur u.
♦ r1/ On remarquera que t o h est distinct de h o t pour tout k distinct de 1. Cette dernière transformation correspond à OM' = k(OM + u) = kOM + ku : dilatation de centre O, de rapport k de vecteur ku. Ci-dessous :
le "chemin bleu" illustre la dilatation t o h : M → M1 = h(M) → M' = t(M1).
le "chemin vert" correspond à h o t : M → M2 = t(M) → M" = h(M2).
➔ On remarque globalement une configuration triangulaire de Thalès : [M1M"] est l'image de [MM2] par h.

♦ r2/ Le plan (ou l'espace) étant rapporté à un
repère d'origine O, on peut ramener la dilatation de centre A à une dilatation
de centre O : AM' = kAM + u
⇔ OM' - OA = k.(OM -
OA) + u
⇔ OM' = k.![]() OM
+ v avec v = u + (1 - k).OA.
OM
+ v avec v = u + (1 - k).OA.
♦ p21/ Muni de la loi de composition des application, l'ensemble des dilatations constituent le groupe des homothéties-translations, souvent note HT(ε) et f ∈ HT(ε) si et seulement si son endomorphisme associé φ est une homothétie vectorielle v → kv, k ≠ 0. Les translations sont caractérisées par k = 1, c'est à dire φ = idE.
∗∗∗
Vérifier que HT(ε) est un
sous-groupe distingué
du groupe affine GA(ε)
☼
| La transvection : |
Lorsque ε est de dimension n (n ≥ 2), considérons un hyperplan Φ de ε (sous-espace affine de dimension n - 1, plan dans le cas n = 3) de direction Δ (plan vectoriel dans le cas n = 3) et un vecteur u de Δ. Munissons ε d'un repère affine d'origine O. Une équation cartésienne de Φ est de la forme h(M) = 0 où M symbolise l'usage de l'équation appliqué à ses coordonnées; h(M) est un scalaire nul si et seulement si M est un point de Φ. Le choix de l'équation h étant fixé :
La transvection
T de base Φ, de
vecteur u ∈ Δ, est l'application qui à tout point M de
ε associe
le point M' = T(M) défini par MM' = h(M).u
• r1. MM' = h(M).u revient à exprimer OM' = OM + (ax + by + cz + ... + k).u où ax + by + cz + ... + k = 0 est une équation de Φ.
♦ p22/ Avec les notations ci-dessus, la transvection est une bijection affine d'endomorphisme associé φ : v → v + h(v).u (transvection vectorielle) où h(v) représente l'équation cartésienne de Δ appliquée à v, c'est à dire celle de Φ privée de son terme constant k, et ses points invariants sont ceux de sa base Φ.
♦ p23/ La transvection réciproque possède les mêmes base et direction et sa transvection vectorielle associée est v → v - h(v).u.
Preuve : pas de preuve ! ce résultat est géométriquement est bien évident.
Preuve : soit O un point choisi comme origine des coordonnées, O' son image par T, M un point de ε d'image M'. O'M' = O'O + OM + MM' = -h(O).u + OM + h(M).u = OM + [h(M) - h(O)].u. Or, h(M) = ax + by + cz + ... + k et h(O) = k, donc h = h(M) - h(O) = ax + by + cz + ... est une forme linéaire des coordonnées de M correspondant à l'équation de Δ : T est affine d'endomorphisme associé φ = idE + h.u. Montrons que T est une bijection : l''espace E étant de dimension finie, il suffit de montrer que le noyau de φ est réduit à {0}. Soit v ∈ E tel que φ(v) = 0. Supposons donc que v + h(v).u = 0. Si v ∈ Δ, alors h(v) = 0 donc v = 0, sinon h(v) ≠ 0 et v = - h(v).u ; v serait donc colinéaire à u : contradictoire, cette hypothèse n'est pas envisageable.
♦ p24/ Choisissons une base de E comme réunion d'un vecteur w n'appartenant pas à Δ, placé en première position, et d'une base de Δ (l'hyperplan vectoriel dirigeant Φ) dont le premier vecteur est u. En notant h la valeur de la forme linéaire sur les coordonnées d'un vecteur de E (correspondant à l'équation de Δ), La matrice d'une transvection vectorielle est alors de la forme :

Preuve : φ est la somme de l'application identique et de φ : v → h(v).u. Avec la convention adoptée, dans le cas n = 2 on a φ(w) = h(w).u , de coordonnées (0,h) et φ(u) = h(u).u = 0 car u vérifie la forme linéaire h. Lorsque n = 3 : φ(w) a pour coordonnées (0, h,0). Les deux autres vecteurs ont pour image 0 par φ puisqu'ils sont élément de Δ.
➔ La permutation des rôles des vecteurs w et u permettent d'écrire 2 matrices élémentaires dans le cas n = 2 et 6 dans le cas n = 3 en remarquant que ne peut appartenir à la diagonale principale. Ces matrices de transvection sont qualifiées d'élémentaires. On notera aussi que leur déterminant est 1.

➔ Par définition de la transvection T, M et N désignant deux points de ε, d'images M' et N' par T :
• r2. MM' = 0 ⇔
h(M) = 0 : les points invariants par T sont les points de Φ.
• r3. a) (MM') // Φ;
b) Les vecteurs MM' et
NN' sont colinéaires et éléments de Δ, autrement dit
(MM') // (NN')
c) MM' = NN' ⇔
h(M) = h(N) ⇔ MN = M'N' ⇔ (MN) // Φ;
(M et N
appartiennent à un même plan parallèle à Φ)
Lorsque n = 3, considérons le plan Φ d'équation x + y + z = 1; son plan directeur Δ a pour équation x + y + z = 0. Soit M(a,b,c) vérifiant a + b + c = α et N(d,e,f), vérifiant d + e + f = β. Les coordonnées de MN vérifient alors (a - d) + (b - e) + (c - f) = α - β qui est un vecteur de Δ si α = β, auquel cas h(M) = h(N) et (MN) // Φ.
• r4. Les remarques 2 et 3 précédentes permettent la construction géométrique de l'image d'un point quelconque M connaissant celle d'un autre point. Ci-dessus, cas de gauche, (MN) est parallèle à Φ; selon r2, connaissant M', on obtient N' comme image de N par la translation de vecteur MM'. Ci-dessus, à droite, (MN) coupe Φ en K qui, selon r3, est invariant par T. La transvection étant une bijection affine, l'image de la droite (KM) est la droite (KM') contenant N', et le parallélisme de (MM') et (NN') fournit N'.
| Décompositions usuelles d'applications affines : |
1) La symétrie centrale plane de centre O est une rotation d'angle π (180°) et peut aussi s'interpréter comme la composée de deux symétries axiales d'axes perpendiculaires sécants en O (la 1ère étant arbitraire) :

2) Toute translation de vecteur v peut s'interpréter comme la composée de deux symétries orthogonales d'axes parallèles, la première étant arbitraire. Ci-dessus : (d) // (d'), (d) ⊥ v, 2HH' = v.

3) Dans le plan, la composée de deux symétries axiales d'axes respectifs concourants d et d' est une rotation dont l'angle orienté est égal au double de l'angle ^(d,d'). Inversement toute rotation peut se décomposer sous cette forme, la première symétrie étant arbitraire.

» Application au triangle orthique
4)
s et idε désignant respectivement une symétrie affine et l'application identique, l'application définie par p = ½(idε + s) est une projection affine (» combinaison linéaire d'applications affines). En effet p o p = ¼(idε + s) o (idε + s) = ¼(2idε + 2s) = ½(idε + s) = p. Le schéma ci-dessous illustre cette propriété : M' désignant s(M), p(M) est le milieu de [MM'].