
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
 Philosophe
et savant universel, René Descartes, sieur du Perron, naquit en Touraine à la Haye, à la limite du
Poitou, aujourd'hui appelée La Haye-Descartes. Il sera élevé par sa grand-mère
maternelle (à qui il doit le titre de Seigneur du Perron,
»
réf. 3), car sa mère mourut (1597) à la naissance de son cinquième enfant.
Philosophe
et savant universel, René Descartes, sieur du Perron, naquit en Touraine à la Haye, à la limite du
Poitou, aujourd'hui appelée La Haye-Descartes. Il sera élevé par sa grand-mère
maternelle (à qui il doit le titre de Seigneur du Perron,
»
réf. 3), car sa mère mourut (1597) à la naissance de son cinquième enfant.
Descartes fit ses études au collège de la Flèche (Sarthe) fondé par Henry IV en 1607 (tenu par les Jésuites, l'établissement deviendra école militaire dès 1764). En cette école, il se lia d'amitié avec Mersenne. Après des études de droit, Descartes fit de nombreux voyages en Europe. Sa rencontre et son amitié avec le physicien hollandais Isaac Beeckman (1588-1637) fut sans doute décisive dans la suite de sa vie et de sa pensée scientifique et philosophique. Renonçant à publier "Le Monde", œuvre plus audacieuse encore que celle de Galilée qui venait d'être condamné par l'inquisition pour avoir prétendu, suivant en cela Copernic, que la Terre tournait sur elle-même et autour du Soleil, il publie, en 1637, son célèbre Discours de la méthode pour conduire correctement la Raison et chercher la Vérité dans les Sciences et en application, trois essais scientifiques novateurs : Dioptrique (lois de la réfraction), Météores, Géométrie.
Descartes développa une philosophie basée sur la science et le raisonnement déductif. Il affirma son célèbre "cogito, ergo sum" (je pense, donc je suis) et estima pouvoir démontrer scientifiquement l'existence de Dieu, ce qui lui vaudra quelques déboires avec l'Église.
| Travaux en algèbre, mise en place de nos notations modernes : |
Ses écrits sont en français. Dès cette époque, les mathématiciens commencent à abandonner le latin au profit des langues nationales au détriment, dans une certaine mesure, de la portée universelle des mathématiques dont le latin était la langue véhiculaire chez tous les mathématiciens européens. Son intérêt pour l'algèbre pourrait être né de la lecture des œuvres en la matière de François Viète, Stifel et Clavius, ces deux derniers publiant en latin.
Initié par Viète, l'usage de lettres pour désigner des quantités numériques est adopté par Descartes qui utilisa nos notations actuelles, comme, par exemple :
x, y, z, ...pour les inconnues dans la résolution d'équations.
a, b, c pour les paramètres (quantités connues).
l'exposant pour les puissances : comme x3 plutôt que xxx. » Chuquet , Wallis
Une expression comme 2x3 - 5x2 = 6x - 3 est écrite :
2x3 - - 5xx
![]() 6x - - 3
6x - - 3
On voit que le carré garde encore curieusement un statut particulier : xx et non pas x2. La persistance de cette notation se trouvera d'ailleurs encore chez d'Alembert.
Le signe
![]() , en forme de alpha renversé, signifie
est égal
à : notre notation d'aujourd'hui (=), due à
Recorde
n'est pas encore en usage.
, en forme de alpha renversé, signifie
est égal
à : notre notation d'aujourd'hui (=), due à
Recorde
n'est pas encore en usage.
La soustraction est notée au moyen de deux tirets successifs.
➔ Descartes utilisa l'expression nombre imaginaire (1637) pour désigner les nombres complexes (ainsi qualifiés par Gauss) et énoncera le théorème fondamental de l'algèbre : une équation polynomiale de degré n admet n solutions -si l'on tient compte des solutions complexes et fausses (négatives).

On voit là que Descartes n'accorde pas aux quantités
négatives le statut de nombre
Ci-dessus, x + 5 = 0 signifie que x désigne une grandeur dont le défaut de quantité est 5. L'équation x4 - 4x3 - 19x2 + 106x - 120 = 0 possède 3 vraies solutions : 2, 3, 4 et une fausse qui est 5.
| La naissance de la géométrie analytique et l'usage des coordonnées : |
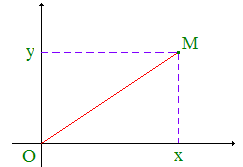 Dans
sa Géométrie (1637,
Dans
sa Géométrie (1637,
Le concept (non le terme) de coordonnées, dont la paternité revient sans doute à Léonard de Vinci, va révolutionner l'étude des lignes courbes ou courbes géométriques (que Leibniz rebaptisera algébriques) : courbes dont l'équation peut se ramener à une forme polynomiale, comme par exemple la parabole dont une équation cartésienne peut se ramener à la forme simple y = x2.
La notion de coordonnées selon d4alembert et de nos jours : »
L'étude des "touchantes" (tangentes) aux courbes et de leurs extremums devient un des problèmes majeurs des mathématiques. Elle conduira au calcul différentiel de Newton et Leibniz.
Les termes d'abscisse, d'ordonnée et de coordonnées n'est pas encore utilisé. Pascal qui utilisa avec brio ce nouvel outil dans l'étude de sa roulette, ne parla que d'ordonnée. Il faudra attendre Leibniz (1692) puis d'Alembert et son encyclopédie.
Les nombres négatifs n'ont toujours pas le statut de nombre :
Tout comme en algèbre, Descartes ne considérait que des "coordonnées" positives en raisonnant sur les mesures de segments d'une figure donnée et s'arrangeant à choisir son repère (droites sécantes jouant le rôle d'axes) de sorte que les coordonnées restent positives : selon l'héritage euclidien la géométrie traite de grandeurs, non de nombres.
D'ailleurs, à propos des équations, Descartes parle de « racines fausses ou moindres que rien » pour désigner celles qui s'avéreraient négatives. Ce qualificatif semble apparaître pour la première fois un an plus tard, en 1638, dans une lettre de Jean de Beaugrand à Mersenne, sous forme de pamphlet contre Descartes.
i Jean de Beaugrand (1584?-1640) : mathématicien français, ami de Fermat mais ennemi de Desargues et de Descartes qu'il accusait de plagier Viète. Membre de l'Académie parisienne de Mersenne, Beaugrand se fit de nombreux ennemis et fut lui-même soupçonné de nombreux plagiats.
➔ Négatif est emprunté au latin negarer = nier, negativus = qui nie, pour exprimer le refus de tels nombres et s'opposant à positif, terme utilisé en philosophie à la même époque pour signifier un caractère d'existence objective, posé comme vérité, du latin posere = poser, positivus = qui exprime une qualité (Correspondances, » réf.2)
Et, ci-dessous, où le Méthodique Impertinent (M.I.) désigne Descartes, accusé d'avoir plagié Viète sans le comprendre... (voir la suite sur le site Gallica, Correspondances, » réf.2) :
C'est avec les nombres complexes, dits alors imaginaires et s'opposant aux nombres réels, que les nombres négatifs s'imposeront avec le fameux i2 = - 1. Les notions d'axe et de mesure algébrique d'un segment ne sont pas encore nées.

» Bombelli , Carnot , Gauss (forme a + bi) , Dedekind , Cantor
Étonnamment, d'Alembert, plus d'un siècle plus tard, considère les nombres négatifs avec circonspection. Il écrit :
« dire que la quantité négative est au-dessous du rien (c'est à dire zéro), c'est avancer une chose qui ne se peut pas concevoir ».
| Repère cartésien : |
Sur le nom de Descartes, on a construit l'épithète cartésien : un esprit cartésien est un esprit méthodique, qui a le sens de l'analyse, de la rigueur.
Dans le plan, un repère cartésien est un triplet (O,u,v), où O est le point origine des coordonnées (cartésiennes), les vecteurs u et v sont non colinéaires (donc non nuls) et constituent une base du plan. Cette appellation est cependant anachronique : les vecteurs n'étaient pas encore "inventés". Mieux vaudrait appeler repère cartésien un repère affine (O,I,J), triplet de points tels que OI et OJ sont non colinéaires. Le produit cartésien de deux ensembles E et F désigne l'ensemble des couples (x,y) où x est élément de E et y élément de F.
Les vecteurs (le terme est d'Hamilton) apparaissent progressivement dans une longue et complexe genèse à la fin du 18è siècle. C'est un concept né des sciences physiques (force, vitesse et accélération) dans le grand renouveau de la géométrie lié à l'introduction des nombres négatifs (géométrie analytique) et l'usage des nombres complexes. On parle alors de segments orientés ou de lignes dirigées (sur une droite) avec Argand , Carnot , Chasles , Möbius. La formalisation dans le plan et l'espace apparaîtra avec Bellavitis, puis Hamilton, Gibbs et Grassmann.
Vecteurs du plan (exposé élémentaire) : »
| Équation cartésienne : |
Relative à une courbe ou une surface, il s'agit dans le plan (resp. dans l'espace) d'une relation de la forme f(x,y) = 0 (resp. f(x,y,z) = 0).
Pour la droite passant par A(1,3), d'ordonnée à l'origine -4, une équation cartésienne est y = 7x - 4.
Pour le plan de l'espace passant par A(1,1,2), B(1,0,1) et C(0,2,1), une équation cartésienne est : 2x + y - z = 1
Pour la sphère de rayon 1, centrée à l'origine des coordonnées (surface de R3), de point générique M(x,y,z), une équation cartésienne est x2 + y2 + z2 - 1 = 0.
» Descartes énonça, sans doute le premier, que toute équation du second degré en x et y est celle d'une conique.
Les coniques selon John Wallis : »
| Un théorème de Descartes sur les équations polynomiales : |
En appelant variation d'un polynôme P, tout changement de signe entre deux termes consécutifs de P, alors :
Le nombre de solutions positives de
l'équation P(x) = 0 ne peut excéder le nombre de
variations.
Quant aux solutions négatives, elle ne peuvent
excéder, en nombre, celui des variations de l'équation
P(-x) = 0.
C'est un résultat fort important concernant l'existence et la séparation des racines d'une équation algébrique qu'étudieront les français Rolle, Lagrange, Budan de boislaurent, Fourier et Sturm.
| Folium de Descartes : |
Cette courbe (du latin folium = feuille, ) fut "inventée" par Descartes (1638, dans une correspondance à Mersenne) afin de mettre en évidence la faiblesse de la méthode de Fermat dans la recherche des extremums d'une courbe algébrique.
C'est une cubique dont une équation cartésienne est :
x3 + y3 = 3kxy (k est un paramètre réel)
Étude de la courbe : » » Folium simple , bifolium , trifolium , quadrifolium
|
Ovales de Descartes : |
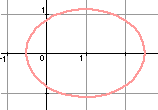 Ce
sont des courbes
définies en coordonnées
bipolaires que Descartes fut
amené à étudier dans ses recherches sur la
réfraction des rayons lumineux et publiées dans Dioptrique (1637). Le limaçon
de Pascal, les
coniques,
à l'exception de la parabole,
en font partie :
Ce
sont des courbes
définies en coordonnées
bipolaires que Descartes fut
amené à étudier dans ses recherches sur la
réfraction des rayons lumineux et publiées dans Dioptrique (1637). Le limaçon
de Pascal, les
coniques,
à l'exception de la parabole,
en font partie :
| Formule de Descartes-Euler : |
Cette célèbre formule lie les nombres de (F)aces, (S)ommets et (A)rêtes d'un polyèdre convexe :
F + S - A = 2 » la preuve d'Édouard Lucas

Polyèdres réguliers : »
Notion de topologie combinatoire : »
| Relation de Descartes : |
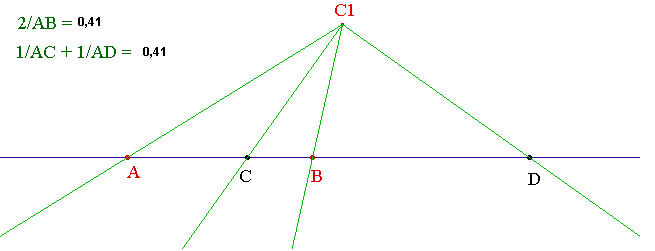
Il s'agit de la formule de géométrie relative à quatre points en division harmonique : pour que les points C et D soient conjugués harmoniques de A et B, il faut et il suffit que :
![]()
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déplacer A et B. Déplacer C1,
déplacera C et D : justifier !
➔ Pour en savoir plus :
La Géométrie sur Gallica, pages 297 et
suivantes de la pagination :
https://gallica.bnf.fr/ark:/12148/btv1b86069594/f381.image.r=La+G%C3%A9om%C3%A9trie+Descartes+1637.langFR
Les Correspondances sur Gallica, publiées sous la direction de Darboux par
Charles Adam et Paul Tannery (frère de Jules
Tannery).
http://gallica.bnf.fr/ark:/12148/bpt6k20744x/f510.image.r=Oeuvres+Descartes.langFR
L’oeuvre mathématique de Descartes dans La
Géométrie, par André Warusfel
http://philosophie.ac-creteil.fr/IMG/pdf/Geometrie.pdf
Le Monde de Mr Descartes ou le Traité de la
Lumière et des autres principaux objets des sens, sur Gallica :
http://gallica.bnf.fr/ark:/12148/bpt6k5534491g/f4.item.r=.zoom
Quelques réflexions sur Descartes et les mathématiques
:
http://www.erudit.org/revue/philoso/1995/v22/n2/027339ar.pdf
René Descartes, Seigneur du Perron, explications sur
le site de l'hôtel Le Pigeonnier du Perron :
http://www.lepigeonnierduperron.com/fr/page/l-historique-de-la-batisse