ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

LÉVY Paul Pierre, français, 1886-1971

Après des études secondaires au lycée Saint-Louis, Paul Lévy intégrera l'École Polytechnique. Il en sort major (1904). Trois plus tard, il est ingénieur des Mines (ENS des Mines de Paris). Tout en enseignant aux Mines de Saint-Étienne, il prépare sa thèse de doctorat qu'il soutiendra (1912) devant Hadamard, Picard et Poincaré.

Lévy enseigna à l'École des Mines de Paris jusqu'en 1951 ainsi qu'à l'École Polytechnique (de 1920 jusqu'à sa retraite). Il fut récipiendaire du prix Poncelet de l'Académie des sciences (1936) et sera élu à ladite Académie en 1964, succédant ainsi à Hadamard.

Pour la petite histoire, Lévy épousa la fille d'Hadamard et la fille de Lévy, Marie-Hélène, épousa Laurent Schwartz (cf. la 1ère référence ci-dessous).

Ses travaux porteront sur l'analyse fonctionnelle (on lui doit ce terme,1922) après les travaux novateurs de Fredholm, Volterra et Fréchet sur ce sujet initié par Euler et, essentiellement, suite à ses recherches sur la théorie des erreurs, sur le calcul des probabilités dans la théorie des variables et processus aléatoires ( processus markoviens) comparées à celle, toute récente en physique, du mouvement brownien (on lui doit aussi cette appellation).

Lévy est, avec le mathématicien américain Doob, à l'origine du concept de martingale intervenant en théorie du potentiel et, avec Poincaré, de la fonction caractéristique d'une variable aléatoire.

  Markov , Kolmogorov , Bachelier , Malliavin

Fonction caractéristique d'une variable aléatoire :

Ce sujet relève, dans son cas général, de la théorie de la mesure. Dans le cas simple d'une variable numérique continue X de densité f, sa fonction caractéristique est l'intégrale de Fourier :

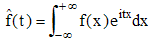
Il s'agit donc de l'espérance mathématique E(eitX) = E(cos tX) + iE(sin tX) de la variable t eitX. Dans le cas de la loi normale, centrée et réduite, un calcul (un peu difficile : intégrale complexe) fournit :

On démontre que les coefficients ak du développement en série entière de la fonction caractéristique sont les moments de X (espérances mathématiques de Xk).

Transformation de Fourier :                  Intégrale de Gauss :

Notion de martingale :

Le concept de martingale, prend sa source dans les jeux d'argent. Sur le plan étymologique, une martingale était une chaussure du 15è siècle (chausses à la martingale) de forme aberrante. Depuis le 18è siècle, dans les jeux d'argent, jouer une martingale consiste à jouer le double de la mise précédente tant que l'on a perdu.

Aussi aberrant que cela paraisse, on est sûr de récupérer sa mise, à condition d'avoir une fortune illimitée ! En effet, si la première mise m est perdue, on joue 2m. Si on gagne, tant mieux, sinon, on joue 4m et ainsi de suite. Si on gagne au n-ème jeu, la dernière mise n'est pas perdue (la perte de mise au coup k est 2k-1 x m), le gain relatif est alors :

2n-1m - (m + 2m + ... + 2n-2m) = 2n-1m - (1 + 2 + ... + 2n-2)m = m

Vous récupérez ainsi votre mise et le gain associé au coup. Mais si vous n'êtes pas imposé à l'ISF, le pari reste très risqué... D'une façon générale, une martingale est une stratégie permettant d'augmenter ses gains dans un jeu de hasard.

Concept de martingale dans la théorie des processus stochastiques :

Il n'est pas possible de développer le concept de martingale dans le cadre de cette chronologie. Ce sujet demande des connaissances préalables solides en théorie de la mesure (algèbres de Borel) et du calcul intégral au sens de Borel-Stieltjes. Pour les initiés, rappelons cependant brièvement quelques notions :

  Considérons un espace probabilisé (W,,p), un processus stochastique (Xt), famille de variables aléatoires de paramètre t positif (le temps par exemple) et une famille croissante (au sens de l'inclusion) (t) de sous-tribus de . Le processus (Xt) est dit adapté à (t) si Xt est t-mesurable pour tout t.

Concrètement, si t est le temps, les t correspondent aux événements antérieurs à l'instant t. Les Xt mesurables sont les variables dont l'état ne dépendent que de l'état de W dans la période antérieure à t. La croissance des t s'interprète comme un apport d'information sur le processus au cours du temps.

  Soit une sous-tribu de . Si X est une variable aléatoire admettant une espérance mathématique E(X), c'est à dire intégrable sur W au sens de p, on démontre qu'il existe une unique variable aléatoire -mesurable Y (à une égalité presque sûre près) telle que pour tout F de , on ait :

On parle d'espérance conditionnelle de X sachant : Y est une variable aléatoire, non un nombre comme dans le cas de l'espérance mathématique. On note généralement E(X|) la variable Y.

  Ceci étant, on dira qu'un processus stochastique numérique (Xt) adapté à (t) est une martingale (resp. sous-martingale, sur-martingale) si les Xt sont intégrables et pour tout (s,t) : Xs = E(Xt|s) presque sûrement   (resp. , ).

Très (très) grossièrement et (un peu) concrètement... : Lorsque s < t, s s représente l'évolution de W dans la période antérieure à s. La valeur moyenne estimée des Xt (dans le futur t) connaissant l'état de W dans la période antérieure à s, n'est autre que Xs.

Pour en savoir plus :

Ford  Riesz Marcel
© Serge Mehl - www.chronomath.com