ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 CHASLES Michel,
français, 1793-1880 |
Polytechnicien,
Michel Chasles obtient son doctorat sous la houlette de Poisson (1814). Officier du génie, cet illustre géomètre professa la mécanique
et la géodésie à l'École
polytechnique puis obtint une chaire de géométrie "supérieure"
créée (1846) à son intention à la
Sorbonne (université de Paris).
Parallèlement aux travaux de Möbius, Plücker et von Staudt en Allemagne, il complète, par une approche synthétique (non analytique, usant des transformations projectives, dualité, principe de continuité) la géométrie projective que Poncelet et Gergonne avaient déjà rénovée, une trentaine d'années auparavant, en reprenant les travaux de Desargues.
Le principal de son œuvre sera publié dans son Traité de géométrie supérieure (1852). Chasles publia également nombre de ses travaux dans les Annales de Gergonne et dans le journal de Liouville (sections coniques, courbes gauches).
Élu à l'Académie des sciences en 1851, Chasles fut le premier président de la Société mathématique de France, dès sa fondation en 1872, aujourd'hui association loi 1901 pour l'avancement et la propagation des études de Mathématiques pures et appliquées.
Il fut également membre à titre étranger de la Royal Society dès 1854 et reçut la déjà convoitée médaille Copley de ladite société en 1865 pour ses travaux innovants en géométrie, un prix pourtant en principe octroyé aux physiciens et biologistes.
| Les transformations homographiques : |
Cherchant à généraliser les résultats de
Poncelet sur l'homologie
dans le cadre de la géométrie projective, Chasles,
indépendamment de
Möbius, recherche les transformations (Chasles parlait
de déformation) du plan et de
l'espace susceptibles de transformer un point (resp. une droite, un plan) en un
point (resp. une droite, un plan) tout en conservant ce
qu'il appela
le
rapport anharmonique (ou
birapport, de quatre points alignés (»
réf. 1,
page 695 et suivantes).
L'objectif étant, connaissant les propriétés d'une figure, d'en déduire celle de son image homographique. Par exemple, comme l'écrit Chasles (» réf. 1, mot clé = homographie) , « étant données certaines propriétés du cercle ou de la sphère, en conclure les propriétés correspondantes des sections coniques ou des surfaces du second degré », ou encore « connaissant quelques cas particuliers d'une certaine propriété générale d'une figure, en déduire cette propriété générale».
Il leur donne le nom d'homographies (1837), forgé à partir du grec (homos = semblable et graphikos = action d'écrire ou dessiner). Möbius les qualifia de transformations projectives.
Dans l'espace euclidien ε à trois dimensions, les transformations géométriques de ε (bijections) conservant le birapport, dites transformations homographiques ont pour expression cartésienne (tous les coefficients étant réels) :
On notera que les dénominateurs de X, Y et Z sont les mêmes. Dans le cas du plan, on aura :
La perspective (projection centrale), l'homologie (dans le cas de l'existence d'une droite invariante point par point) en sont des cas particuliers. L'inversion géométrique n'en est pas une : il s'agit d'une transformation de Möbius.
Dans leur généralité, les transformations homographiques ne sont pas des applications affines : elles ne conservent pas le barycentre, ni le parallélisme.
➔ Inversement, les transformations affines (applications affines bijectives) conservent le birapport et peuvent s'interpréter comme transformation homographique dans le cas trivial m = n = p = 0.
∗∗∗
Un cas simple de transformation homographique :
étude
analytique d'une perspective plane
A cette époque, celle de Chasles et de Möbius, la distinction entre la géométrie euclidienne et la géométrie projective restait cependant floue. Il manquait à cette dernière une mise en place indépendante passant donc par une définition axiomatique et une claire distinction entre propriétés métriques et projectives. Ce sera une des taches de l'allemand Von Staudt. Klein parachèvera l'ensemble de ces recherches en 1872, avec son célèbre programme d'Erlangen et la théorie des groupes de transformations.
| La géométrie algébrique : |
Les travaux géométriques de Chasles sur les figures homographiques et la notion d'invariant d'un groupe de transformations initiée par Klein évoqués ci-dessus, marqueront la naissance d'une nouvelle théorie susceptible de s'affranchir du contexte projectif : la géométrie algébrique, unissant l'étude des objets géométriques et l'algèbre, au sens usuel et au sens des structures algébriques de ces objets géométriques, avec un noyau central : la topologie.
Le souci premier était la classification des courbes et des surfaces algébriques de l'espace R3 (définies par des équations polynomiales), auquel s'attacha Hesse, en Allemagne, et plus généralement (ultérieurement) celle des variétés, avec la recherche de propriétés invariantes par transformations bicontinues (invariants topologiques) et l'étude de leurs intersections, donc l'étude de polynômes et de leurs racines communes. En remplaçant le corps des réels par celui des complexes, les mathématiciens ont pu obtenir des résultats plus généraux (eu égard au théorème de d'Alembert).
Développée en Italie, en particulier par Véronèse, Cremona (et ses fonctions birationnelles), Castelnuovo, Enriques et en Allemagne par Clebsch, Hesse et Max Noether d'un point de vue projectif dans les cas réel et complexe, la géométrie algébrique subit une refondation au moyen de l'algèbre commutative (anneaux, théorie des idéaux) par Zariski (États-Unis), van der Waerden en Hollande, Grothendieck, Weil, Serre et Samuel en France, dans laquelle on s'affranchit du contexte projectif au profit de variétés abstraites de dimension finie définies sur des corps commutatifs quelconques.
La géométrie algébrique actuelle peut empiéter sur la géométrie différentielle dans la mesure où les variétés étudiées peuvent posséder des propriétés différentielles facilitant leur étude et leur classification. Les travaux de S. Novikov ou la théorie de la déformation de Kodaira-Spencer est un exemple d'une telle immixtion.
➔ On pourra s'initier à la géométrie algébrique contemporaine en étudiant les références 8 à 11 in fine.
Cette branche très féconde des mathématiques actuelles rejoint également l'arithmétique (théorie algébrique des nombres) en s'intéressant à la recherche des points à coordonnées rationnelles sur une courbe ou une surface et une application des plus retentissantes de cette nouvelle et puissante branche des mathématiques sera la démonstration du grand théorème de Fermat par le mathématicien anglais Andrew Wiles en 1995.
»
Max Noether , Lefschetz
,
Langlands
, Zariski , Grothendieck
,
Atiyah , Hodge
van der Waerden ,
Mumford ,
Kontsevich ,
Kodaira , Voisin ,
Birkar...
| Homothétie & figures semblables : |
Les termes homothétie, homothétique sont également dus à Chasles (on lit omotéssi mais omotétique..., du grec homos = semblable et thesis = position). Formellement, on appelle homothétie de centre O, de rapport k (k réel non nul), l'application qui à tout point M du plan ou de l'espace associe le point M' tel que :
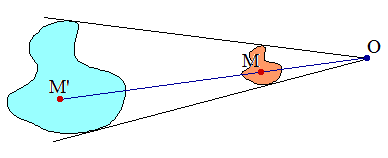
Deux figures F et F' sont homothétiques s'il existe une homothétie transformant l'une en l'autre. Si |k| > 1, on parle d'agrandissement; si |k| < 1, c'est une réduction.
Homothétie en tant qu'application affine : »
! Tout dépend du "sens" de la transformation... Si F' est l'image de F par une homothétie de rapport k > 1, alors F' est un agrandissement de F et, dans ce cas, F est une réduction de F' par l'homothétie inverse (réciproque) de rapport 1/k. D'autre part, ne pas confondre avec le signe de k. Ci-dessous F' est un agrandissement de facteur (ou de coefficient) 3 = |-3|.
Plus généralement, deux figures sont semblables si elles peuvent se correspondent par la composée d'une homothétie et d'une rotation (similitude directe) ou d'une homothétie et d'une symétrie axiale -ou par rapport à un plan dans le cas de l'espace- (similitude indirecte).
| La célèbre formule de Chasles et les mesures algébriques : |
Soit A et B deux points d'un axe Δ, droite graduée munie d'une origine et d'un sens positif de parcours; la mesure algébrique du segment [AB], notée aujourd'hui AB, est le nombre algébrique xB - xA où xA et xB désignent les abscisses respectives de A et B sur Δ :
AB = xB - xA = OB - OA
La notation AB apparut dans les années 1920-1930 pour désigner un vecteur d'origine A, d'extrémité B, également appelé à l'époque segment dirigé. On parle aujourd'hui de segment orienté ou de bipoint. Chasles notait ab le segment orienté d'origine a, d'extrémité b et posait ba = -ab en énonçant, pour trois points a, b et c d'une même droite, la relation : ab + bc + ca = 0. » ci-dessous le texte original
i Un bipoint est un couple de points généralement noté (A,B). Il est toujours "orienté" en ce sens qu'il est à distinguer de (B,A). Si l'ordre d'écriture des points n'intervient pas dans le contexte, on parle alors d'une paire de points : c'est un ensemble de deux éléments noté {A,B}
Premières notions de vecteur : » Calcul vectoriel élémentaire dans le plan : »
La formule de Chasles peut ainsi s'exprimer :
Pour tous points A, B et C : AB = AC + CB ou encore : AB = CB - CA
La formule est aussi attribuée à Möbius mais fut utilisée par Wessel et Argand bien auparavant dans la construction du plan complexe. Elle se généralise aux vecteurs (du plan ou de l'espace) que Bellavitis (avec sa théorie des équipollences), Hamilton, Grassmann et Gibbs mettront bientôt en place : en utilisant la notation italique gras pour les vecteurs, elle exprime que pour tous points A, B et C de la droite, du plan ou de l'espace, on a la relation :
AB = AC + CB ou encore : AB = CB - CA
|
➔ Pour en savoir plus :
Michel Chasles par Eugène Rouché, sur le site SABIX de l'École polytechnique : http://www.sabix.org/bulletin/b5/chasles.html
Aperçu historique sur l'origine
et le développement des méthodes en géométries (1837) :
http://books.google.fr/ebooks/reader?id=SZIKAAAAYAAJ
Traité de géométrie supérieure de
Michel Chasles (1852) :
http://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-99637
Les Géométries, par Lucien Godeaux, Éd. Armand Colin - Paris, 1937.
Géométries affine, projective et euclidienne
Collection formation des enseignants et formation
continue -Ed. Hermann - Paris, 1983.
Géométrie
Rapport sur les progrès de la géométrie, par
Michel Chasles (1870) sur le site Gallica de la BnF :
http://gallica.bnf.fr/ark:/12148/bpt6k5790435r/f6
Géométrie algébrique in
Dictionnaire des mathematiques
: algèbre, analyse, géométrie, pages 473-495
ENCYCLOPÆDIA UNIVERSALIS, tome1, Éd. Albin
Michel, Paris - 1998.
La géométrie algébrique, par Roger Apéry : http://www.numdam.org/article/BSMF_1943__71__46_0.pdf
Introduction à la géométrie algébrique, par
Olivier Debarre
(univ. Paris), spécialiste en géométrie algébrique :
http://www.math.ens.fr/~debarre/DEA99.pdf
Introduction à la géométrie algébrique, par Rafael Guglielmetti, École polytech.
Lausanne
(variétés algébriques, topologie de Zariski) :
http://rgug.ch/medias/math/geometrie_algebrique.pdf
Géométrie algébrique par Daniel
Perrin (univ. Orsay-Paris Sud), CNRS Éditions, 2001
Ce livre est proposé en accès limité sur Google Livres à l'adresse
https://books.google.fr/books?id=ZKFxGOkUT8sC
Green
