
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Ce docteur en médecine écrivit en 1484 un traité, Triparty en la science des nombres, portant sur les équations polynomiales, les radicaux et l'arithmétique commerciale, remarquable par la précision du langage et du symbolisme utilisé. Suivi de 156 problèmes, dont certains empruntés à Bachet de Méziriac et à son contemporain italien Luca Pacioli (né la même année), mais traités de façon nouvelle que l'on peut qualifier d'algébrique, le livre de Chuquet ne fut pas imprimé, ce qui explique sa moindre audience, comparée par exemple à celle de Pacioli avec sa Summa, 10 années plus tard.
➔ L'invention par l'allemand Johannes Gutenberg de la presse à imprimer (1434) encouragea la traduction et l'impression des textes mathématiques (Apollonius, Diophante) et astronomiques (Ptolémée) de la Grèce antique et accéléra la mise en place d'un symbolisme algébrique judicieux et mieux adapté aux contraintes typographiques : Rudolff, Stifel, Widmann, Riese (Allemagne), Viète, Girard, Descartes, Kramp (France), Recorde (Angleterre), Pacioli, Bombelli (Italie).
| Notations nouvelles de l'algèbre : |
Chuquet manipule des nombres et des exposants négatifs et énonce ce qu'il est convenu d'appeler aujourd'hui la
règle des signes pour les nombres qualifiés (c'est à dire positifs ou négatifs), qui était cependant connue des mathématiciens indiens depuis le 7è siècle et brillamment remis en lumière par l'algébriste arabe As-Samaw'al au 12è siècle, complétant, dans le cadre du système décimal positionnel, les travaux d'Abu Bakr Al-Karaji.Règle des signes selon Rolle : » Règle des signes selon d'Alembert : »
Toutefois les nombres négatifs, ainsi qualifiés par Jean de Beaugrand en 1638, n'ont pas encore le statut de nombre et les fractions sont inférieures à l'unité. On peut considérer que ce statut sera accordé par Euler dans son Introduction à l'Algèbre (1770) et, définitivement par Gauss. D'Alembert, pourtant très moderne dans son usage de la géométrie analytique, n'est guère indulgent vis à vis de leur existence et de leur usage :
∗∗∗
On a 2/3 < 3/4. Vérifier que l'on a alors 2/3 <
5/7 < 3/4. Prouver alors ce résultat énoncé par Chuquet :
deux fractions données
encadrent celle obtenue en ajoutant entre eux les numérateurs et les
dénominateurs. Autrement dit :
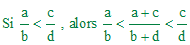
Pour Viète, comme pour Cardan et Descartes, ces nombres apparaissent comme auxiliaires de calcul : la solution d'une équation est positive, les solutions négatives sont rejetées.
Dans une équation d'inconnue x, Chuquet utilise :
➔ L'égalité n'est pas encore codée : on doit le signe = à l'anglais Recorde .
Deux exemples :
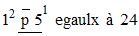
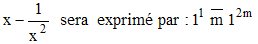
On parle d'algèbre syncopée, car faisant encore appel plus à une écriture usuelle abrégée qu'à un véritable symbolisme. Avec Stifel, Riese, Bombelli, Stevin et Viète, Chuquet s'inscrit comme précurseur des notations algébriques usuelles qu'établiront Wallis, Descartes et Newton. Son œuvre ne fut cependant réellement reconnue qu'au 19e siècle.