ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» Rappel : dans cette page, et dans ChronoMath en général, l'écriture en gras ou italique gras, comme OA, désigne un vecteur.

On se propose de montrer tout d'abord que dans un triangle ABC, d'orthocentre H, de centre de gravité G et dont le centre du cercle circonscrit (Γ) est noté O, on a :

• (1) OH = OA + OB + OC : relation d'Euler.
• (2) OH = 3OG  et par suite O, H et G sont alignés : sur la droite d'Euler contenant le centre du cercle des neuf points, milieu de [OH].

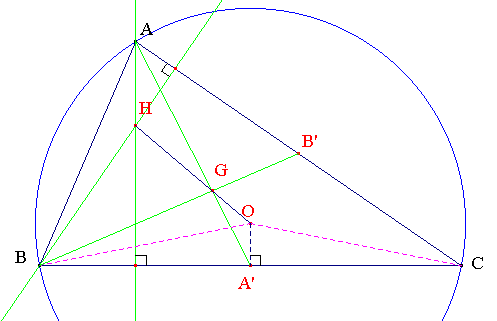
Preuves : Soit K tel que OK = OA + OB + OC. Notons A' le milieu de [BC]. (OA') est la médiatrice de (BC). Il est clair (règle du parallélogramme) que OB + OC = 2OA' et la relation (1) peut alors s'écrire : AK = 2OA'. Or (OA') // (BC), par conséquent (colinéarité), le point K est situé sur la hauteur issue de A. Or, on montrerait évidemment de même que K est situé sur les hauteurs issues de B et C. K est donc à l'intersection des hauteurs du triangle ABC : K n'est autre que l'orthocentre H de ce triangle.

 ➔  Remarquer que l'on vient de démontrer de façon détournée que les hauteurs d'un triangle sont concourantes.

Une autre façon semblable d'aborder cette question, ayant le mérite de ne pas utiliser la relation cherchée est la suivante : soit K tel que AK = 2OA'. (OA') étant la médiatrice de (BC), on a AK = OB + OC. Or (OA') // (BC), par conséquent (colinéarité), le point K est situé sur la hauteur issue de A. Or, on montrerait évidemment de même que K est situé sur les hauteurs issues de B et C. K est donc à l'intersection des hauteurs du triangle ABC : K n'est autre que l'orthocentre H. Repartant alors de AK = OB + OC, on déduit OK - OA = OB + OC, donc OK = OH = OA + OB + OC.

Afin d'obtenir la relation (2), il suffit d'utiliser la relation de Chasles dans la relation (1) en faisant intervenir le point G, centre de gravité du triangle, sachant que, c'est bien connu... : GA + GB + GC = 0.

On suppose connu que les hauteurs d'un triangle sont concourantes (» preuve élémentaire) en un point H, appelé orthocentre du triangle, et que les médianes d'un triangle se coupent au tiers à partir de leur pied au centre de gravité G du triangle (» preuve).

On montrera facilement que :

a/  les milieux A', B' et C' des côtés du triangle ABC sont respectivement les images des sommets A, B et C par l'homothétie f de centre G de rapport -1/2.

b/  f transforme les hauteurs en les médiatrices des côtés.

c/  f transforme H en O. On retrouve en conséquence la relation selon laquelle OH = 3OG : O, G et H sont alignés. La droite portant ces points est la droite d'Euler.

Dans le triangle un ABC on note A', B', C' les pieds des médianes, A1, B1, C1 les pieds des hauteurs, K, L et M les milieux de AH, BH et CH. On note Ω le milieu de [OH] et H' le second point d'intersection de (AH) avec le cercle (Γ).

d/ A' est le milieu de [A"H] et A1 est le milieu de [HH']. On retrouve ainsi que :

Le symétrique de l'orthocentre d'un triangle par rapport aux côtés du triangle est situé  sur le cercle circonscrit.
» orthocentre et cercle circonscrit

Preuve : dans le triangle AHA", O est le milieu de [AA"] et (OA') // (AH). Donc (OA') est une droite des milieux dans AHA" et par conséquent A' est le milieu de [A"H]. Le triangle AH'A" est rectangle en H car [AA"] est un diamètre de (Γ). Par suite, (BC)//(A"H') et A' étant le milieu de [A"H], A1 est celui de [HH'].

e/ On considère maintenant l'homothétie h de centre H qui transforme A" en A'. Montrons que h(O) = Ω et que l'image de (Γ) par h est le cercle circonscrit au triangle A'B'C' que nous notons (γ). Le rayon de ce cercle est donc la moitié de celui de (Γ).

Preuve : l'homothétie h est de rapport 1/2. Ω étant le milieu de [OH], on a HΩ = ½HO, donc h(Ω) = O. L'image par h du cercle passant par A, B et C est le cercle passant par A', B' et C'. On a prouvé ci-dessus que A' est le milieu de [HA"], donc h(A") = A'. De même h(B") = B' et h(C") = C' : (γ) contient donc les milieux des côtés du triangle ABC.

f/  Le cercle (γ) passe par A1, B1, C1 d'une part et K, L, M d'autre part : c'est le cercle des neuf points.

Preuve : la question d/ montre également que (γ) contient les pieds A1, B1 et C1 des hauteurs des côtés du triangle ABC. Considérons le triangle AHA". (OK) joint les milieux des côtés [AH] et [AA"]. Donc (OK) // (HA"). On déduit de ce résultat que le quadrilatère OKHA' est un parallélogramme dans lequel une diagonale est [OH] de milieu Ω. Ce point est donc le milieu de [A'K] : ce qui prouve que K est un point de (γ) diamétralement opposé à A'.  On prouverait de même que L et M sont sur ce cercle : (γ) est le cercle des neuf points.