ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

MEUSNIER Jean-Baptiste Marie Charles, français, 1754-1793

Élève de Monge à l'Académie militaire de Mézières, il se fit tôt remarquer par ses remarquables capacités en mathématiques et entrera à l'Académie des sciences en 1784 pour sa contribution dans l'étude locale des surfaces. Mais il continue sa carrière militaire. Lieutenant-colonel du génie sous la révolution, Meusnier organisa les armées de la toute jeune République. Général de division (1792), il fit face aux armées prussiennes et mourut à Cassel (Kastel en allemand, près de Mayence), touché par un boulet de canon.

Poursuivant les premiers travaux, initiés par Euler et Monge sur la courbure des surfaces, Meusnier nous a laissé d'importants résultats.

Théorème de Meusnier :

Considérons une section quelconque (oblique ou non) d'une surface Σ par un plan (P) suivant une tangente (t) en un point M de Σ.

 ➔  Par section oblique, on entend une section par un plan ne contenant pas la normale en M à la surface. A contrario, une section normale la contient.

Dans ces conditions :

Le rayon de courbure au point M de cette section est la projection sur (P) du rayon de courbure
de la section normale au même point suivant la même tangente (t).

Le cas de la sphère illustre clairement ce théorème : la section normale en M est ici le grand cercle de diamètre [AM]. Le triangle ABM est rectangle en B et (OC) est une droite des milieux dans ce triangle. Ainsi OMC est rectangle en C.

Le rayon de courbure de la section normale est R = OM, celui de la section oblique est r = CM et on a r = R.cosθ. En terme de courbure, on retrouve ici que la courbure normale est :

Kn = 1/OM = cosθ/r.

Les recherches de Meusnier sur ce sujet seront complétées au siècle suivant par Dupin et, principalement par Darboux et Ribaucour, au moyen de la géométrie différentielle :

Autres résultats de Meusnier :  »      

Notion de surface minimale (jusqu'au début du 20è siècle, on parlait de surface minima) :

Par rotation autour de l'axe des abscisses, une chaînette engendre une surface de révolution , appelée caténoïde ou alysséïde (du latin catena = chaine / du grec alusis = chaîne) dont les courbures moyennes sont nulles en tout point : une telle surface, délimitée par une courbe fermée, présente une aire minimale.

C'est un résultat obtenu par Lagrange et Gauss. Dans son traité Leçons sur la théorie générale des surfaces (1887), Darboux aborde ce sujet qui fut généralisé à des espaces euclidiens de dimension finie avec les travaux de Serge Bernstein.

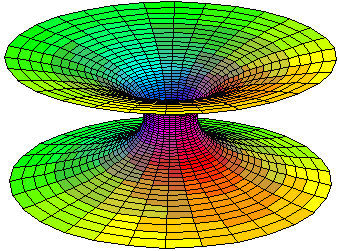
Euler fut le premier (1749) à s'intéresser à ce sujet relevant du calcul des variations. Meusnier et Euler établirent que le caténoïde est la seule surface minimale de révolution. L'équation, dans le plan, de la chaînette étant y = a.cosh(x/2), l'équation du caténoïde peut s'écrire, en coordonnées curvilignes :

x = a.cosh(u/a).cos v , y = a.cosh(u/a).sin v , z = u

où a est une constante. Ci-dessus, au moyen du logiciel de Denis Monasse, on a choisi a = 2; u varie de -5 à 5 , v varie de 0 à 2π.

Un théorème de Meusnier :   

La courbure moyenne est nulle en tout point d'une surface minimale

Courbure moyenne et totale, calcul dans le cas 3D euclidien :  »

Meusnier a montré (1776) que l'hélicoïde (ci-contre), mot à mot en forme de spirale (du grec helix = spirale), concrétisé par la vis d'Archimède, est la seule surface minimale réglée.

On le génère par le déplacement d'une droite perpendiculaire à l'axe d'un cylindre droit de rayon r, passant par cet axe par et une hélice circulaire tracée sur le cylindre. Son équation peut s'écrire, en coordonnées curvilignes :

x = αu.cos v , y = αu.sin v , z = β.v

où α et β sont des constantes; u varie entre 0 et r , v décrit R.

» Ci-contre, à gauche, v varie de 0 à 6π (soit 3 "tours de vis"). à droite, observatoire (risques incendie) et relais téléphonique à Lunel (Hérault).

Surface réglée  :  »         » Lancret

Étonnantes sont les surfaces engendrées par la nature :    

On connaît bien le jeu d'enfant consistant à produire des bulles de savon à partir d'un cerceau trempé dans de l'eau savonneuse. La bulle se détache du cerceau en prenant une forme instable, puis en l'absence de vent, devient parfaitement sphérique. Ce faisant, pour le même volume d'air intérieur, elle a minimisé sa surface extérieure.


à volume égal, la sphère est la forme la plus économique en terme d'aire

Dans un solide quelconque, perçons un trou ou bien fabriquons un contour fermé quelconque en fil de fer (courbe de l'espace). Trempons-le dans un liquide savonneux et ressortons-le de sorte qu'une surface savonneuse referme l'orifice ou le contour. C'est une surface d'aire minimale : la nature cherche à minimiser son travail de rebouchage... elle n'est pas prodigue.

Problème de Plateau :  »         Problème de Bernstein :  »

» Maupertuis , Bonnet , Serret , Frenet , Darboux

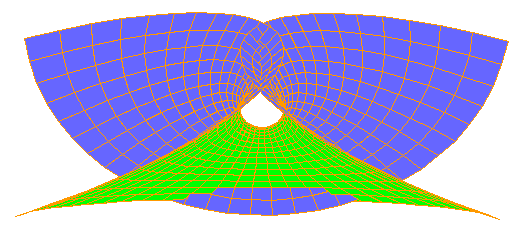
Surfaces de Scherk et d'Henneper :   

Les surfaces minimales de l'espace 3D euclidien ne sont pas légions. Ce n'est qu'en 1835 que deux autres telles surfaces furent découvertes par le mathématicien et astronome allemand Heinrich Scherk (1798-1885). Tracée par le logiciel de Denis Monasse (» réf.3 ci-dessous), voici une période de la 1ère surface bi-périodique de Scherk, suivie de celle de son compatriote Alfred Enneper (1830-1885) découverte en 1863 par usage de sa paramétrisation, dite de Weierstrass-Enneper, un outil de fabrication, en quelque sorte, de surfaces minimales de l'espace 3D euclidien (» réf.8).

ezcos(x) = cos(y), soit : x = u, y = v, z = ln(cos(u)) - ln(cos(v)), u et v décrivant ]-π/2,+π/2[
» la seconde surface peut être représentée par sin(z) = sinh(x)sinh(y), » réf.2

x = u - u3/3 + uv2, y = v -v3/3 + u2v, z = u2 - v2, u et v décrivant ]-2,+2[

 ➔   Pour en savoir plus :

  1. Leçons sur la théorie générale des surfaces (T1) sur le site de l'université du Michigan (USA) :
    http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0001.001;cc=umhistmath

  2. Surfaces de Scherk : La page du site MathCurve de Robert Ferréol :
    https://www.mathcurve.com/surfaces.gb/scherk/scherk.shtml
    La page de Wikipedia (en) : https://en.wikipedia.org/wiki/Scherk_surface

  3. Surface2, un de Denis Monasse : http://denis.monasse.free.fr/denis/logiciels/Surface2.jar

  4. Mathématiques savonneuses, par Paul Laurain sur le site Images des mathématiques (CNRS) :
    http://images.math.cnrs.fr/mathematiques-savonneuses.html

  5. Surfaces minimales, par Pierre Bérard, univ. J. Fourier, Grenoble, 2011 :
    https://www-fourier.ujf-grenoble.fr/~pberard/D/surfaces-minimales-beamer.pdf

  6. Quelques aspects des surfaces minimales, par Alexis Michelat et Sheng Yuan Zhao ENS) :
    https://www.math.ens.fr/enseignement/telecharger_fichier.php?fichier=1432

  7. Surfaces minimales et lignes de courbures, par Pierre Gallais sur le site Images des mathématiques (CNRS) :
    http://images.math.cnrs.fr/Surfaces-minimales-et-lignes-de.html

  8. Enneper surface : https://en.wikipedia.org/wiki/Enneper_surface

Carnot  Parseval
© Serge Mehl - www.chronomath.com