ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Démarche scientifique,
problème ouvert
& enseignement » la démarche scientifique |
Un problème ouvert est une conjecture (énoncé avancé comme vrai mais non prouvée) soutenue par une communauté scientifique et non mise en défaut à ce jour. Par exemple :
une célèbre conjecture de Goldbach (1742) énonce que tout entier pair autre que 2 est la somme de deux nombres premiers.
Il n'existe pas de nombres parfaits impairs, conjecturé par Euler.
➔ La notion de problème ouvert trouve aujourd'hui sa place en pédagogie (comme, depuis les années 1980, à l'IREM de Lyon et de Grenoble). Son objectif est d'initier à la démarche scientifique dans la recherche, par petits groupes, de la solution d'un problème dont l'énoncé est court, formulé en langage ordinaire, compréhensible par tous, sans indications de méthode ou solution, permettant de faire des essais, de conjecturer, et ne devant faire appel, pour sa résolution, qu'à des outils adaptés au niveau et aux savoirs du public concerné. Une telle situation d'apprentissage comprend quatre étapes que l'on peut résumer par :
comprendre / s'approprier l'énoncé;
chercher / essayer ↔ écarter;
conjecturer / tester
prouver / si contradiction, aller en 2.
| Exemple (classe de 5e) : on donne 2 points distincts, puis 3, puis 4, puis 5. |
Combien peut-on, dans chaque cas, tracer de segments distincts ?
Et si on en donne n (n étant un entier au moins égal à 2) ?
Variante : conjecturer une formule donnant le nombre de diagonales d'un polygone. » polygones
|
Il n'est pas dit ici que l'on doit limiter l'enseignement des mathématiques qu'à ce type de recherche : |
Principalement au collège, les questions doivent, à part égale, être ouvertes (elles ne renferment pas le résultat) et fermées (elles renferment le résultat). Ayant travaillé sur la division en 6è, posons en contrôle le petit exercice suivant :
« 600 photocopies ont coûté 24 euros; combien coûte une seule photocopie ? »
Trop facile : tout le monde est content. On pose la division 600 divisé par 24; chouette, ça tombe juste : une photocopie coûte 25 euros. Aucun ne s'inquiète de ce coût exorbitant alors qu'on a payé, au total, ne l'oublions pas, 24 euros... : en maths, déjà en 6ème, on ne donne pas un sens à un résultat. Rassurons-nous, l'euro n'est pas en cause. Le même problème posé en francs conduisait aux mêmes scores. Un résultat ça se trouve, ça ne s'interprète pas et on passe, content, à l'exercice suivant. Lors de la correction, vexés, déçus, la moitié des élèves de la classe sera dégoûtée des maths...
∗∗∗
Les maths, c'est pas la vie : c'est l'avis
des élèves... dès la 6ème ! Pourquoi ? La faute à qui, la faute à quoi ? C'est
une question récurrente (terme mathématique bien connu) comme on dit
maintenant à la télé... Sans doute un excès de géométrie dès l'école primaire :
trop d'abstraction, déconnexion avec le réel, trop de définitions d'objets
(toute la panoplie des triangles, des quadrilatères,
des parallélépipèdes,
...)
»
programme CM1/CM2
Si l'on avait écrit :
Combien de centimes font 24 euros ?
600 photocopies ont coûté 24 euros; calcule en centimes le prix d'une seule photocopie.
On aurait plus de 70% de réussite à cet exercice : les élèves ont divisé 2400 par 600 et trouvé 4 centimes. On l'a compris : dans une division, on divise toujours le plus gros nombre par le plus petit. C'est dire que l'élève est passé sur pilote automatique : il ne donne toujours pas de sens au résultat. S'il se trompe dans les "zéros" en trouvant 400, il répondra 400 centimes sans sourciller.
➔ Sans être totalement fermées, les questions permettent à un élève désireux de bien faire de ne pas avoir 0 à ce petit problème. Si l'on veut mieux assurer les scores de réussite, rien n'interdit d'écrire quelque chose comme :
Montre, en posant la division, que
600 ÷ 24 = 25.
Explique maintenant sans faire la division que 600 ÷ 2400 = 0,25.
Tu es bien d'accord que 2400 ÷ 600 = 4; explique maintenant sans faire la division que 24 ÷ 600= 0,04.
Voici un petit problème :
« 600 photocopies ont
coûté 24 euros. On veut calculer, en centimes, le prix d'une seule photocopie. »
Parmi les résultats précédents, lequel conduit à la solution de ce problème ?
Justifie ta réponse.
En soulignant en centimes, on tente d'éviter une
mauvaise lecture de la consigne. Mais on n'empêchera toutefois pas, l'expérience
le prouve,
la question «
M'sieur, la réponse, on la donne en centimes ? » ...
| Revenons à nos problèmes ouverts : |
Il s'agit ainsi d'appliquer le schéma ci-dessous résumant la démarche scientifique selon Claude Bernard, physiologiste et philosophe français, 1813-1878 :
 |
 |
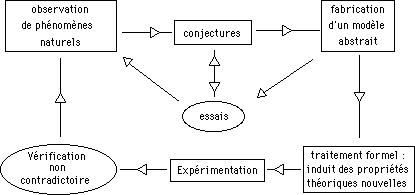Il est regrettable que les programmes actuels (et passés, et sans doute à venir), principalement au collège, ne soient pas un peu plus orientés vers ce type de pédagogie. Les savoirs disciplinaires sont introduits sans autre objectif que l'élève doit être capable de... ou, parfois, par acquit de conscience, il est rajouté "en liaison avec les autres disciplines" :
- Le cosinus en 4ème...
- La propriété de Thalès en 4ème...
- Les transformations (géométriques) au collège...
- Les vecteurs en 3ème...
- La réintroduction du PGCD en 3ème...
- La pyramide en 4ème et 3ème... sujet ringard ou nécessité pédagogique ?
- ...
|
L'ennui est, qu'à ces niveaux, les autres disciplines n'utilisent pas les mathématiques... : |
Il se forge ainsi rapidement dans l'esprit des collégiens que les maths, ça sert à rien... Leur usage au collège est très réduit. Il se limite, « dans les autres disciplines », à quelques calculs élémentaires de proportionnalité, quelques graphiques et, en 3ème, en sciences physiques, à d = vt (mouvement uniforme), P = UI (électricité élémentaire) : encore de la proportionnalité dans une société mercantile où, à part le plein d'essence, on ne la rencontre guère...
| Les sciences physiques : |
c'est au collège une matière essentiellement
expérimentale et
finalement plus simple à appréhender que la technologie;
en classe de 4ème, un usage très timide des puissances de 10, parachutées par le professeur, conduit les élèves à exprimer le lendemain, "en maths", que 53 c'est 5000 car on écrit 5 suivi de 3 zéros;
en classe de 3ème, la notion de vecteur s'identifie à une fléchette au dessus d'une lettre ou deux...
On a alors généralement des bonnes notes; on aime ! Et maman ou papa exprimeront que c'est bizarre d'avoir de si mauvaises notes en maths alors qu'en physique ça marche si bien...
|
L'enseignement des mathématiques reste purement disciplinaire et encyclopédique : |
Les professeurs ayant enseigné dans les années 1970-80 ont en mémoire les ravages de l'enseignement des mathématiques "modernes" au collège et au lycée. Axiomatique pour ne pas dire bourbakiste, cet enseignement qui ne laissait aucune place à l'intuition et à un entendement visuel (pouvant s'exprimer par un dessin) fut étonnamment introduit par Lichnerowicz et sa commission qu'il dirigea de 1967 à 1972 avec la "complicité" de Jean Dieudonné. Étonnamment car Lichnerowicz était aussi (et surtout) un physicien, lequel exprimait vouloir faire des mathématiques en rapport avec le réel, raison pour laquelle il s'intéressa à la physique mathématique.
Depuis 1985, le retour à l'algèbre élémentaire et de la géométrie euclidienne permet à l'élève de mieux appréhender les objets mathématiques. Malheureusement les contenus restent encyclopédiques et décrochés de tout lien avec l'idée que les mathématiques sont l'outil incontournable de toutes les sciences, quoiqu'en pense M. Claude Allègre...
- En 4ème : on a ajouté, à l'aube du 21è siècle, la propriété de Thalès, comme si celle de Pythagore ne suffisait pas dans le méli-mélo algébro-géométrique déjà présent, alors qu'il sont (les élèves de 4è) :
à la décharge des programmes, il faut reconnaître que le non apprentissage quasi systématique des leçons, vu l'abandon général de l'interrogation orale, traumatisante et vexatoire pour l'élève (puisqu'il n'a rien appris) joue un rôle indéniable dans ces lacunes... |
Quant à la trigonométrie -tout à fait indésirable en 4ème encore par manque total d'applications à ce niveau- comment justifier la survivance du fameux cosinus, vieux relent de la projection orthogonale, avant celle du sinus (cosinus = sinus associé). De surcroît, cet objet mathématique abstrait se résume chaque année à une désastreuse utilisation de la touche cos, et pire cos-1 ou Acs (fonction réciproque) avec une confusion entre l'angle et sa mesure en l'absence de toute notion de fonction.
- En 3ème :
on factorise à tour de bras des expressions bien faites "pour que ça marche";
on résout automathiquement des équations "produit nul";
on confond avec délice, depuis 40 ans et jusqu'en 1èreS, a2 - b2 avec (a - b)2;
on supprime l'étude intuitive des droites du plan au profit des fonctions linéaires et affines !
On explique à ces
malheureux enfants que f(x) ne veut
pas dire "f facteur de x" : pas le temps de parler de
Leibniz ou de
Lagrange... et
va que je te trouve l'expression de f(x) = ax + b sachant que f de ceci =
cela. Dans un contrôle, mettez un g(x) au lieu du f(x), ça c'est
méchant.
La grande majorité des élèves sont à une année-lumière de tout ce fatras débridé et inutile. Et comme cela ne suffit parfois pas à les détourner complètement des mathématiques :
on bâcle des angles inscrits et au centre;
on rajoute l'intersection
d'un prisme avec un plan parallèle à une arête;
»
le professeur lui-même serait parfois bien
embêté de prouver que tel plan est effectivement
parallèle à une arête donnée...
on compose des translations et des rotations;
et on termine avec des notions de statistique appelées pompeusement "gestion de données".
Par
contre, en CM2, on a supprimé la division décimale laissant les
enfants dans une vision béate d'un monde
où
tout est entier et beauté
pythagoricienne.
à
l'heure de l'euro et des arrondis/conversions, on s'étonne.
Il est
vrai que les professeurs des écoles n'ont généralement pas vraiment appliqué cet
allégement des programmes...
On fonce à 130 sur un chemin de campagne et au bout, il n'ont rien compris, rien assimilé, détestent les maths, adorent la techno (qui rime avec musique), veulent faire de l'informatique (qui rime avec jeu) tout en étant incapables du moindre raisonnement logique. Mais ils auront le brevet même avec 8/40 à l'épreuve afin de respecter les 80% de réussite académique. Le résultat, c'est que M'sieur, les maths ça sert à rien...
La preuve,
au yeux des élèves ?
Les footballeurs;
Star-Académie, PopStars ou Loft-story;
Le prof d'histoire-géo qui se vante d'avoir été nul en math et d'avoir quand même "réussi";
Papa "qu'a eu 2 au brevet et qu'est chef de service à la DDE";
Maman ? les maths ? pareil. Et pourtant elle est "chef d'agence à la Caisse d'Épargne".
...
Chez un bon nombre d'entre eux, on a « la haine des maths ». Elle se transmet dans les lycées et on se plaint officiellement qu'il n'y a plus de scientifiques, ni de candidats au CAPES de maths, etc.
Déjà dans les années 1950, Bertrand Russell, éminent philosophe et mathématicien, remarquait que contrairement aux temps de la Grèce ancienne et de la Renaissance, faire montre de connaissances mathématiques relève de l'exotisme. Le fort en maths est une bête curieuse, un intello. La culture est littéraire, artistique. On peut y inclure l'histoire, mais pas celle des sciences...
De
nos jours, lors d'un jeu télévisé de "culture générale", si vous tombez sur une
question musique, ce ne sera pas Bach, Mozart ou Beethoven :
dès la
première question, vous allez vous planter sur le dernier titre en vogue du
groupe Téléphone et en littérature, ce sera la dernière BD de Mœbius,
alias Jean Giraud (1938-2012), ne pas confondre avec le
mathématicien...
Est-il vraiment nécessaire de
faire ingurgiter aux élèves des collèges
et des lycées tant de connaissances académiques dont
ils n'ont que faire ? Avant d'être des élèves,
ils sont des enfants soucieux, aujourd'hui plus que naguère,
d'une certaine forme de rentabilité immédiate, d'un
pragmatisme de l'apprentissage.
N'est-il pas bien plus formateur pour cette citoyenneté dont on parle tant aujourd'hui de les amener, par le problème ouvert ou par des situations similaires (via l'histoire des sciences tout particulièrement), à se poser des questions, essayer, conjecturer et, par là, à énoncer ou construire eux-mêmes des résultats ou des objets mathématiques (accessibles à leur entendement) où ils se sentiraient (un peu) plus concernés ? Avant de les gaver (expression-élève bien appropriée...), apprenons-leur à apprendre en motivant leur imagination.
Stella Baruk (cf. référence ci-dessous) a bien raison depuis 30 ans. On fabrique des automathes déréglés et on exige des élèves des connaissances académiques excessives et rébarbatives. Dans notre enseignement, les mathématiques sont une fin alors qu'elles devraient être un moyen, un outil. La dessus, on peut être d'accord avec Claude Allègre lorsqu'il ne confond pas mathématiques et programmes de mathématiques...
➔ Pour en savoir plus :
