
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 D'origine
russe d'une famille émigrée aux Etats-Unis, dont son père
Tobias (qui étudia à Paris) fut professeur
de mathématiques, Dantzig fit ses études à l'université du Maryland (côte est
des Etats-Unis), où enseigna son père, ainsi qu'à Berkeley (Californie) où
il fondera le Centre de Recherche Opérationnelle
(Operations Research Center).
D'origine
russe d'une famille émigrée aux Etats-Unis, dont son père
Tobias (qui étudia à Paris) fut professeur
de mathématiques, Dantzig fit ses études à l'université du Maryland (côte est
des Etats-Unis), où enseigna son père, ainsi qu'à Berkeley (Californie) où
il fondera le Centre de Recherche Opérationnelle
(Operations Research Center).
Dantzig sera nommé (1966) professeur de recherche opérationnelle et de science informatique en la très réputée université de Stanford (proche de San Francisco, Californie). Dantzig y poursuivra ses recherches jusqu'à sa retraite en 1996.
Récipiendaire de nombreuses distinctions en hommage à ses fructueux travaux, Dantzig est élu à l'Académie nationale des sciences des Etats-Unis en 1977.
|
Méthode du simplexe : |
Dès 1947, Dantzig expose son algorithme de résolution de systèmes d'inéquations linéaires à n variables x1, x2, ...xn, s'écrivant matriciellement :
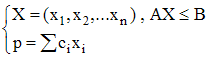
par la méthode dite du simplexe, trouvant de nombreuses applications en théorie des jeux stratégiques : on cherche à optimiser une fonction p, combinaison linéaire des inconnues sous les contraintes définies par les inéquations. Le développement de l'informatique facilitera la résolution de tels systèmes. Depuis Leonid Kantorovitch (1912-1986), prix Nobel d'économie 1975, on parle de programmation linéaire.
Géométriquement, la méthode consiste à cheminer sur les arêtes d'un polyèdre (hyperpolyèdre : dès que la dimension dépasse 3), plus précisément d'un polytope, en cherchant à maximiser (ou minimiser) une fonction économique donnée. Si le polytope est borné, la solution optimale, lorsqu'elle existe, se situe en un sommet du polyèdre.
Convexité et polytope : » Ordre, treillis et simplexe : » » Alicia Boole Stott , Coxeter
Dès la classe de seconde des lycées, les élèves sont amenés à résoudre graphiquement des systèmes d'inéquations linéaires à deux variables utilisant la méthode du simplexe dans le plan :
Illustration de la méthode du simplexe dans le plan (optimisation de la fabrication d'un produit) : »
∗∗∗
Autres exemples (niveau 2nde) dans Chronomath : Abonnement ,
Transporteurs
» Euler , Von Neumann , Tucker , Berge , Villani , Figalli
➔ Pour en savoir plus :