ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

ARCHIMÈDE de Syracuse, grec, -287/-212

Ce célèbre mathématicien, ingénieur et physicien, était un parent du roi Hiéron II, tyran de Syracuse de -270 à -215. Fils d'astronome, ami d'Ératosthène à Alexandrie, il fut un élève d'Euclide d'Alexandrie.

Le qualificatif tyran est ici utilisé au sens premier du terme, c'est à dire, au sens de l'Antiquité grecque, un gouverneur ou un chef d'État exerçant, à la suite d'un coup de force, un pouvoir absolu sans l'assentiment de la population mais sans cruauté systématique a priori...

La passion d'Archimède pour la géométrie s'exprime dans ses livres sur La sphère et Le cylindre où il montre en particulier que la surface de la sphère de rayon R est égale à celle d'un cylindre de même rayon et de hauteur 2R, le volume étant par ailleurs les 2/3 de ce cylindre. Résultats remarquables dont l'illustration, à sa demande, orne son tombeau.

Sa méthode d'exhaustion, proche de la méthode des indivisibles de Cavalieri et du calcul infinitésimal de Leibniz et Newton le conduit à des quadratures comme celle de la parabole.

Dans l'étude du cercle, il calcule implicitement le nombre π, parfois appelé nombre d'Archimède (voir ci-après), en exprimant que le rapport de la circonférence au diamètre est sensiblement 3 augmenté de 1/7.

En mécanique, outre la roue dentée, le palan (également appelé mouflage, démultiplication de la traction par un système de poulies mouflées), la vis sans fin, Archimède inventa des machines de guerre (catapulte, miroirs paraboliques) pour repousser les Romains lors du siège de Syracuse.

C'est au cours de cette bataille qu'il fut tué par un soldat romain. Marcellus, commandant de l'armée romaine, ordonna des funérailles solennelles en hommage à ce grand savant.

Grandes inventions des grecs antiques (sur Dailymotion) :

Ci-dessous, Archimède menacé par un soldat romain. Mosaïque d'Herculanum, ancienne ville romaine, proche de Naples qui fut ensevelie, ainsi que Pompéi, lors d'une éruption du Vésuve en 79 après J.-C.

Le cercle et le nombre d'Archimède :                Divers calculs de p dans ChronoMath

Dans son traité, La mesure du cercle, utilisant la méthode dite des périmètres, Archimède approche la circonférence du cercle par les périmètres de polygones réguliers inscrits et exinscrits en utilisant 96 côtés et donne un encadrement de p tout à fait remarquable eu égard à l'époque et aux moyens de calcul  :

Par cette méthode et un encadrement de 3, Archimède établit :

Le terme de circonférence désigne en fait tant un cercle que son périmètre. On parle aussi de longueur du cercle mais cela n'est pas très correct car un cercle n'a ni début ni fin...On a depuis trouvé des fractions plus proches du célèbre nombre comme 355/113, calcul dû à Metius, que l'on retrouve dans le développement en fraction continue de 3,1415926535...   Ahmes.

En fait, le « nombre d'Archimède », p , n'avait pas encore le statut de nombre : Archimède entendait là le rapport L/d du périmètre du cercle à son diamètre :

    le périmètre du cercle (circonférence) est donc donné par L = p x d
    ou encore L = 2 x p x r.

Ainsi : si désigne l'aire du disque de rayon r, de diamètre d, alors /r² est comme L/d. C'est dire que l'aire d'un disque de rayon r est p x r².

La longueur d'un arc de cercle est proportionnelle à l'angle au centre â correspondant : = pr x â°/180 ou, si â est exprimé en radians, tout simplement : = â x r. De même, l'aire d'un secteur d'ouverture â sera S = pr² x â/360 ou, si â est exprimé en radians : S = r² x â/2.

Pour en savoir plus (périmètre et aire)  :                     Calculs de p dans ChronoMath :

 Archimède prouva aussi l'équivalence entre le problème de la quadrature du cercle et celui de sa rectification (construire un segment dont la longueur est la circonférence d'un cercle donné).

 Machin , Shanks , de Cusa , Euler

  
p : par quadrature approchée du cercle  (TP 5è/4è) ,  p et boîte de conserve (TP CM2/6è)

1.  Un jardinier, qui voulait creuser un bassin circulaire de 3 m de rayon, se décide finalement pour un bassin carré de même périmètre. Quelle sera, à 1 dm près, la mesure du côté de ce bassin ?   Rép : 4,7 m.

2. Un jardinier veut planter des arbustes en bordure d'un massif circulaire de 5 m de rayon en les espaçant de 50 cm.
a) Combien doit-il prévoir d'arbustes ? Rép : Le jardinier doit prévoir 63 arbustes.  
b) Il veut fleurir le massif. Ses sachets de semis permettent de fleurir 3 m². Combien de sachets doit-il prévoir ?
Rép : Le jardinier doit prévoir 27 sachets.

La méthode d'exhaustion et l'axiome d'Archimède :

Archimède établit de nombreuses formules relatives aux aires planes (dont celle située sous un arc de parabole), aux mesures des surfaces (dont celle de la sphère égale à 4 fois celle du cylindre dont la hauteur est égale au diamètre, soit 4pr²) et des volumes (dont celui de la sphère qu'il évalue à sa valeur exacte, soit 4pr³/3).

Ces résultats sont obtenus par la méthode d'exhaustion dont l'initiateur fut Eudoxe et réexposée par Euclide dans ses éléments. Elle repose sur un axiome de continuité, dit d'Archimède, présent dans les Éléments d'Euclide en tant que proposition I du livre X :

En soustrayant de la plus grande de deux grandeurs données plus de sa moitié, et du reste plus de sa moitié, et ainsi de suite, on obtiendra (on finira par obtenir en réitérant le procédé un nombre fini de fois) une grandeur moindre que la plus petite.

Formulation moderne et formulation géométrique de l'axiome :            Méthode d'exhaustion :

Archimède apparaît ainsi comme un génial précurseur du calcul infinitésimal. Ce principe que reprendra Cavalieri au 17è siècle, permettra encore plus tard d'approcher finement les nombres irrationnels et à Dedekind de construire les réels par les "coupures".

Alliée à la théorie des proportions d'Eudoxe, la méthode d'exhaustion conduira Archimède à ce résultat remarquable :

l'aire sous la parabole (délimitée par la corde [AB] et l'arc de parabole) est exactement les 4/3 de l'aire du triangle ABC, C désignant le point de la parabole où la tangente (T) est parallèle à (AB).

 Aire sous la parabole (quadrature de la parabole) : Volume de la sphère : 
 

Miroirs paraboliques :

Archimède connaissait les propriétés focales des paraboles. La légende raconte qu'il utilisait des miroirs paraboliques, les fameux miroirs ardents, constitués de plusieurs miroirs hexagonaux articulés, focalisant les rayons du soleil afin d'embraser les vaisseaux ennemis. Afin d'entretenir le foyer, les Vestales d'Athènes, gardiennes du feu de Vesta, utilisaient un miroir concave recouvert d'une feuille d'or : les rayons du Soleil convergeaient au foyer, concentrant la chaleur.

Étude des miroirs sphériques & paraboliques :

Spirale d'Archimède :

Elle est l'ensemble des points M se déplaçant d'un mouvement uniforme sur une droite en rotation uniforme autour d'un point (ici l'origine).

Spirale d'équation r = t/10 tracée pour t > 0

Son équation polaire est de forme r = a x t  où a désigne un paramètre non nul et t l'angle polaire de M exprimés en radians). Elle aurait en fait été "découverte" par Conon de Samos.   

En savoir plus sur cette spirale :

En physique, on lui doit en particulier les premières lois de l'hydrostatique (poussée d'Archimède) et une étude précise sur l'équilibre des surfaces planes (égalité des moments, principe du levier) et la phrase fameuse :

Donnez-moi un point d'appui, je soulèverai le monde

Le principe du levier illustré au parc de la tête d'or à Lyon (Ensemble pour la paix, Xavier de Fraissinette, 1996)

Ci-contre, deux poids p et p' sont suspendus à une barre (homogène) AB en équilibre, l'équilibre est obtenu si ap = bp'. Ainsi si p est deux fois plus grand que p', alors b = 2a :

 le "bras" de levier est inversement proportionnel à la masse

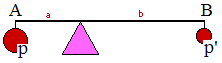
Notons ici que la balance romaine, basée sur le principe décrit ci-dessus, n'est pas d'origine romaine : le nom vient de l'arabe roummana = grenade (le fruit) pour désigner le peson mobile se déplaçant sur la réglette.

ci-dessus, illustration d'une balance romaine (Larousse, 1905)

La découverte de la poussée d'Archimède est liée à Hiéron, roi de Syracuse, qui lui avait demandé de vérifier si sa couronne était faite d'or pur :

Tout corps plongé dans un liquide subit de la part de celui-ci, une poussée exercée du bas vers le haut, et égale, en intensité, au poids du liquide déplacé.

Ayant découvert cette loi en prenant son bain, il se serait précipité nu dans les rues de la ville, en criant Eurêka!...Eurêka! (j'ai trouvé!... j'ai trouvé!).

Une partie d'une copie de son manuscrit fut retrouvé à Constantinople en 1907 sous la forme d'un palimpseste : le texte du parchemin a été gratté et le support réutilisé pour une page de la Bible.

Dans son traité sur le centre de gravité des surfaces planes, Archimède expose magistralement le concept de centre de gravité, également appelé aujourd'hui centre d'inertie, point abstrait où l'on peut considérer que la masse de l'objet s'y concentre et peut être ainsi remplacé, dans les calculs, par ce point pondéré.

Notion de barycentre, calcul de la position du centre de gravité d'un solide :

La vis d'Archimède :

On doit aussi à Archimède (ou à Archytas de Tarente ?), l'invention de la roue dentée (ancêtre de l'engrenage) et de la célèbre vis d'Archimède : utilisée en mécanique, appelée aussi vis sans fin, son principe est utilisé dans la construction de machines utilisées pour faire monter le grain dans les silos, dans la fabrication des vis, des forets et, plus prosaïquement, des tire-bouchons.

Le mouvement, dit hélicoïdal, transmis par une vis sans fin s'interprète comme le composé commutatif R o t d'une rotation R d'axe (d) et d'une translation t dont le vecteur même direction que (d) : c'est un déplacement de l'espace (isométrie positive) appelé vissage. La courbe correspondante est une hélice circulaire, géodésique du cylindre (chemin le plus court entre deux points d'une surface).

C'est à Archimède que l'on doit la définition d'un segment de droite comme le plus court chemin d'un point à un autre : les géodésiques du plan sont les droites de ce plan.

Vissage en tant qu'isométrie : Hélicoïde :

Une caractéristique de cette courbe est que la tangente en chacun de ses points fait un angle constant avec l'axe du cylindre : si l'on développe ("déroule") le cylindre, l'arc AB d'hélice devient un segment. Inversement, un segment devient un arc d'hélice.

 Frenet                    "géodésique" du cube
 

Polyèdres archimédiens ou solides d'Archimède :

Il s'agit de polyèdres convexes dont les faces sont des polygones réguliers convexes (triangle équilatéral, carré, pentagone régulier, ...) dont les côtés ont même mesure et présentant en chaque sommet la même configuration. Catalan les qualifia de semi-réguliers.   Polygone convexe : entièrement situé dans un des demi-plans défini par l'un quelconque de ses côtés.  polygones                                    Polyèdre convexe : entièrement situé dans un des demi-espaces défini par l'une quelconque de ses faces. polyèdres réguliers

Hormis les prismes et les anti-prismes, on en compte 13. Un autre, plus simple, est le cuboctaèdre constitué de 6 carrés et 8 triangles équilatéraux de même côté :

Solides d'Archimède (précisions et figures) :

La trisection de l'angle :

Archimède s'intéressa aussi au célèbre problème de la trisection de l'angle : existe-t-il une méthode purement géométrique (construction "à la règle et au compas") permettant de construire un angle de mesure trois fois inférieure à celle d'un angle préalablement construit ?

Trisection selon Archimède :

Orthocentre : point de concours des hauteurs dans un triangle

Dans un triangle, une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Un triangle a donc trois hauteurs et ces droites son concourantes : elles sont sécantes en un même point appelé orthocentre (du grec orthos = droit), noté ici H comme très souvent. Si un des angles du triangle est obtus, l'orthocentre sera situé "en dehors" du triangle.

Preuve selon Archimède du concours des hauteurs d'un triangle :

Vous pouvez déplacer les sommets A, B et C afin de constater les diverses positions de H (cas particuliers)

Triangle orthique :                  Cercle d'Euler :

Hauteur et médiane dans un triangle rectangle  apprendre à démontrer (5ème)

Construction d'un triangle   cas élémentaires, 4 exercices indépendants (6ème/5ème)

Construction d'un triangle connaissant l'orthocentre   (4ème)

Construction d'un triangle connaissant deux hauteurs    (5ème/4ème)

Construction d'un triangle connaissant un sommet, une hauteur et le centre de gravité    (4ème/3ème)

Construction d'un triangle connaissant l'orthocentre et le centre de gravité    (1ère/Ter)

Orthocentre et cercle circonscrit     (niveau 2nde/1ère)

---

Euclide   Conon

---

© Serge Mehl - www.chronomath.com