
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Racines n-ièmes (énièmes) d'un nombre réel ou complexe | Racines n-èmes de l'unité » programmes JavaScript on line : racines carrées (algébriques) , racines n-èmes (trigonométriques) |
Dans l'ensemble des nombres réels (nombres entiers, nombres fractionnaires, nombres rationnels ou non), on appelle racine carrée d'un nombre x un nombre r tel que r2 = x.
Cette définition implique que x est positif. Sous cette seule condition, 4 et -4 seraient les racines carrées de 16 et on pourrait dire que -4 est la racine carrée négative et +4 la racine carrée positive. En fait, on appelle racine carrée de x le nombre positif r tel que r2 = x :
Étant donné un nombre réel
positif x,
on appelle racine carrée de x le nombre positif r tel que r2
= x.
| Racines carrées d'un nombre complexe : |
Comme il l'a été dit à la page Rudolff, (notation √ de la racine carrée), la positivité de la racine carrée d'un nombre réel est purement historique, car datant d'une époque où les nombres négatifs "n'existaient" pas, à savoir l'époque de Pythagore.
! Cette positivité se justifie aussi pour la possibilité de définir une fonction racine carrée mais elle est non seulement un piège pour les élèves mais aussi une gène dans la généralisation du concept de racine carrée aux nombres complexes car, selon la définition dans C, corps des nombres complexes contenant le corps R des réels :
On appelle racine carrée d'un nombre complexe z tout nombre r dont le carré est z
Par exemple : 1 + i et -1 - i sont les racines carrées de 2i car (1 + i)2 = (-1 - i)2 = 2i
Il suit :
qu'un nombre réel positif x devrait posséder deux racines carrées opposées : √x et -√x;
qu'un nombre réel négatif x devrait posséder deux racines carrées opposées : i√x et -i√x où i désigne le célèbre nombre complexe dont le carré est -1.
Tout dépendra, dans un problème, de savoir si l'on travaille dans C ou non :
dans C, le nombre 4 = 4 + 0i possède deux racines carrées, l'une positive : +2, l'autre négative : - 2;
dans R, la racine carrée de 4 est 2; l'équation x2 = 4 possède deux solutions, à savoir ± √4 = ± 2.
dans R, - 4 n'a pas de racine carrée;
dans C, - 4 possède deux racines carrées opposées : ± 2i.
dans C, - 4i possède deux racines carrées opposées : ±(√2 - i√2).
Racine carrée complexe et surface de Riemann : »
Expression algébrique des racines carrées d'un nombre complexe :
Soit z = a + ib un nombre complexe, a et b réels, b non nul. Il s'agit de calculer les nombres réels x et y tels que z = (x + iy)2. En développant et en identifiant les parties réelle et imaginaire, on obtient a = x2 - y2 et b = 2xy.
En remarquant que x2 + y2 = | (x + iy)2 | = | z | = √(a2 + b2) = m (module de z), on est conduit au système :
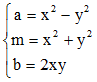
Les deux premières équations fournissent aisément ± x et ± y. La troisième équation permet de savoir si x et y ont même signe ou non suivant le signe de b. D'où, en conclusion :
Si b > 0, les racines carrées de z = a + ib sont :
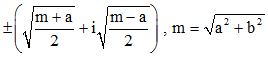
Si b < 0, les racines carrées de z = a + ib sont :
Programme JavaScript :
Le programme ci-dessous calcule la forme algébrique des racines carrées d'un nombre complexe donné sous la forme a + bi. Le programme reconnaît les fractions (données sous forme n/d), fonctions mathématiques (sin, cos, tan, sqrt : racine carrée, ...) et s'efforce de donner des valeurs rationnelles (généralement des approximations) de x2 et y2 puis de x et y, en faisant appel au développement en fraction continue. L'approximation rationnelle trouvée par l'ordinateur doit être lue avec circonspection !!!
| Racines n-èmes d'un nombre réel ou complexe : |
Dans R, l'équation x3 = 8 n'a qu'une seule solution : x = 2; en effet : x3 - 8 = (x - 2)(x2 + 2x + 4) et le trinôme x2 + 2x + 4 n'est pas factorisable dans R puisque son discriminant est -12 < 0 (a non nul).
Dans C, la même équation x3 = 8 possède 3 solutions : x = 2, x = -1 - i√3 , x = -1 + i√3 : ce sont les racines cubiques de 3 dans C, également dites racines troisièmes de 2.
Plus généralement si n désigne un entier naturel non nul, on appelle racine n-ème du nombre complexe z, tout nombre r tel que rn = z.
Théorème :
Tout nombre complexe non nul z possède n racines n-èmes
Ce résultat est évident en tant que conséquence du théorème fondamental de l'algèbre. On le prouve aussi très simplement en utilisant la forme trigonométrique des complexes : soit ρ le module et θ un argument de z défini à 2kπ. On a z = ρ(cosθ + i.sinθ). Posons r = m(cosα + i.sinα), m > 0; selon la formule de Moivre, on a rn = mn(cos nα + i.sinα); par suite : mn = ρ et θ = nα modulo 2π. D'où :
![]()
Ce qui fournit n racines n-èmes distinctes. Vérifions que ces racines ne dépendent pas du choix de θ : si θ' est un autre argument de z, alors θ' = θ + 2k'π, ce qui fournit α' = (θ + 2k'π)/n + 2kπ/n = θ/n + 2(k' + k)/n. Or k et k' sont des entiers relatifs arbitraires, il en est donc de même de k + k' : on retrouve les racines n-èmes α précédemment calculées.
| Les racines n-èmes (énièmes) de l'unité, racine primitive et cas n = 3, 4 et 6, : |
Avec les notations ci-dessus, l'équation rn = 1 conduit à : m = 1 et α = 2kπ/n , k = 0, 1, ..., n-1.
Si n = 3, racines 3èmes, dites cubiques : on a α = 2kπ/3 , k = 0, 1, 2. On note généralement j (notation logique après celle de i) la racine cubique correspondant à k = 1 :
![]()
pour k = 2, on obtient :
➔ Géométriquement, les racines n-èmes de l'unité sont les sommets du polygone régulier Pn à n côtés (n-gone) inscrit dans le cercle unité. Le point unité 1 est un sommet commun à tous les Pn.

On remarque que 1 + j + j2 = 0, ce qui est naturel vu que j est solution de l'équation r3 - 1 = 0, équivalente à (r - 1)(r2 + r + 1) = 0.
Si n = 4, racines 4èmes : on a α = 2kπ/4 = α = kπ/2 , k = 0, 1, 2, 3. On reconnaît là : 1, i, -1 et -i
Si n = 6, racines 6èmes : on a α = 2kπ/6 = kπ/3 , k = 0, 1, 2, 3, 4, 5. On reconnaît là : 1, 1/2 + i√3/2, j, -1, j2,1/2 - i√3/2
Muni de la multiplication, les racines n-èmes de l'unité forment un groupe cyclique isomorphe au groupe additif de l'anneau Z/nZ.
Toute racine n-ème u engendrant ce groupe est dite racine primitive. Si u est une racine primitive, il en est de même de u.
Quel que soit n, 1 n'est pas une racine primitive;
Pour n = 3, c'est le cas de j et j2 = j ; pour n = 4, c'est le cas de i et -i.
Théorème :
a) Soit u, une racine n-ème de l'unité et k un entier naturel. un est primitive si et seulement si n et k sont premiers entre eux : pgcd(n,k) = 1. Ce qui revient à dire que k est inversible dans Z/nZ.
b) Le nombre de racines n-èmes primitives est égal à φ(n), indicateur d'Euler (totient) et constituent un groupe isomorphe aux éléments inversibles de Z/nZ.
Polynôme cyclotomique : » Exercices niveau Terminale et Sup : »
| Programme JavaScript : |
Le programme ci-dessous calcule les arguments des racines n-èmes d'un nombre complexe donné sous la forme a + bi. Le programme reconnaît les fractions (données sous forme n/d), les fonctions mathématiques (sin, cos, tan, sqrt : racine carrée, ...) et s'efforce de donner des coefficients rationnels p/q de l'argument exprimé sous la forme π × p/q en faisant appel au développement en fraction continue.
L'approximation rationnelle trouvée doit être lue avec circonspection : elle ne sera exacte que pour des arguments de a + bi eux-mêmes de la forme π × p/q. Le module ρ1/n commun à ces racines, où ρ désigne le module de a + bi, n'est pas indiqué car sa valeur n'est rationnelle que dans des cas que nous qualifierons de rarissime...