
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
|
Dans un triangle, une médiane est une droite passant par un sommet et par le milieu du côté opposé. Un triangle a donc trois médianes et ces droites sont concourantes en un point appelé centre de gravité car c'est le point d'équilibre du triangle (isobarycentre).

![]()
Si votre navigateur accepte les applets
Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déformer le triangle ABC en
déplaçant les points A, B et C
On se propose de montrer ici que dans un triangle ABC :
Le centre de
gravité G, point de concours des médianes, se situe au tiers des médianes à
partir de leur « pied ». En conséquence, elles sont
concourantes.
![]()
équivalente, au moyen de la formule de Chasles à :
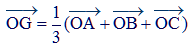
C'est dire que si l'on a A(a,a'), B(b,b') et C(c,c') dans un repère du plan, alors :
xG = (a+b+c)/3, yG = (a'+b'+c')/3
Pour tout point M du plan, le centre de gravité G du triangle ABC est l'unique point minimisant MA2 + MB2 + MC2, somme des carrés des distances de M aux sommets du triangle.
Si tu sèches après avoir bien cherché : »
| Indications : |
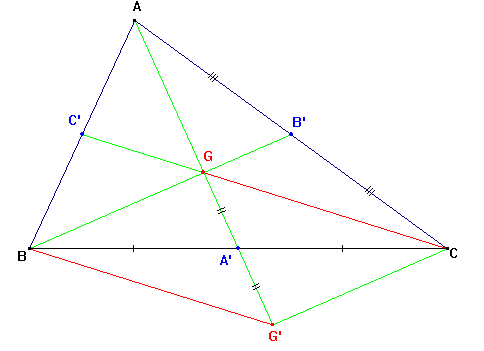
♦ Le 1er résultat se démontre facilement en classe de 4ème. Preuve partiellement développée :
Soit G l'intersection de deux médianes, par exemple celles issues de A et de B, de pieds respectifs A' et B';
♦ Le 2ème résultat se démontre facilement en classe de 3ème. Preuve partiellement développée :
D'où le résultat annoncé.
♦ Le 3ème résultat est basé sur le produit scalaire (classe de 1ère) :
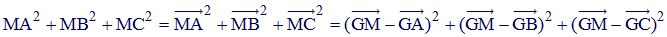
En développant ces carrés scalaires, on obtient :
Or selon le second résultat, la parenthèse est nulle. La somme MA2 + MB2 + MC2 sera donc minimale si et seulement si GM est nul, c'est à dire si et seulement si M est en G.
Cercle d'Euler : » Droite d'Euler : »